深度学习实践第三讲之梯度下降

梯度下降 Gradient Descent

B站 刘二大人 PyTorch深度学习实践-线性模型

为什么要引入梯度

  在上一讲中通过枚举法来找到拟合目标，但是在实际情况中，一仿麦呢难以一开始就确定权重$w$的范围；另一方面，权重可能是多维的，会陷入维度诅咒中。因此，我们希望程序自己去寻找最合适的$w$的值，那么问题就转换成了求使得代价函数$cost(w)$有最小值时的$w$的值，即：
$$w^{\ast }=\underset{w}{\mathrm{argmin}}cost(w)$$
  使用梯度下降可能会陷入局部最优的问题，但事实发现，在深度学习实例中，并没有太多的局部最优点。

寻找w最小值

1. 初始化$w$：随机确定一个$w$的值，作为初始值
2. 判断方向：计算此时的梯度值，梯度的负方向即为下次前进的方向
3. 更新权重：每次向梯度的负方向前进一小步，即$w=w-\alpha \frac{\partial cost}{\partial w}$

$MSE$损失函数梯度计算推导

$$\begin{array}{rl}\frac{\partial cost}{\partial w}& =\frac{\partial }{\partial w}\frac{1}{N}\sum _{n=1}^N(x_n\cdot w-y_n{)}^2\\ & =\frac{1}{N}\sum _{n=1}^N\frac{\partial }{\partial w}(x_n\cdot w-y_n{)}^2\\ & =\frac{1}{N}\sum _{n=1}^{N}2\cdot (x_n\cdot w-y_n)\frac{\partial (x_n\cdot w-y_n)}{\partial w}\\ & =\frac{1}{N}\sum _{n=1}^{N}2\cdot x_n\cdot (x_n\cdot w-y_n)\end{array}$$

拟合目标

本节课的拟合目标是拟合如下数据：

梯度下降拟合目标

源代码：

import numpy as np
import matplotlib.pyplot as plt

# dataSet
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 默认初始权重为1
w = 1

# learning rate
lr = 0.01

# define linear model
def forward(x):
    return x * w

# define cost function (MSE)
def cost(x_data,y_data):
    cost_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)
        cost_sum += (y_pred_val - y_val) ** 2
    return cost_sum/len(x_data)

# compute gradient
def gradient(x_data, y_data):
    grad = 0
    for x_val, y_val in zip(x_data, y_data):
        grad += 2 * x_val * (x_val * w - y_val)
    return grad / len(x_data)

print('Predict (before training)', 4, forward(4))

epoch_list = []
loss_list = []

# training
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    # update w
    w -= lr * grad_val
    print('Epoch: ', epoch, 'w=%.3f' % w, 'loss=%.3f' %cost_val)
    epoch_list.append(epoch)
    loss_list.append(cost_val)

print('Predict (after training)', 4, '%.3f' %forward(4))
print('The linear model is y = x * %.2f' % w)

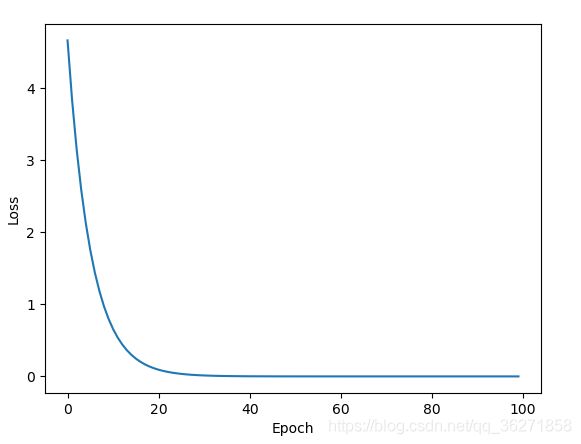
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(epoch_list, loss_list)
plt.show()

结果

Predict (before training) 4 4
Predict (after training) 4 8.000
The linear model is y = x * 2.00

随机梯度下降拟合目标

  梯度下降算法可以解决绝大多数的问题，但在在遇到“鞍点”问题时无法解决。
  鞍点（Saddle point）在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。在泛函中，既不是极大值点也不是极小值点的临界点。
  广义而说，一个光滑函数（曲线，曲面，或超曲面）的鞍点邻域的曲线，曲面，或超曲面，都位于这点的切线的不同边。

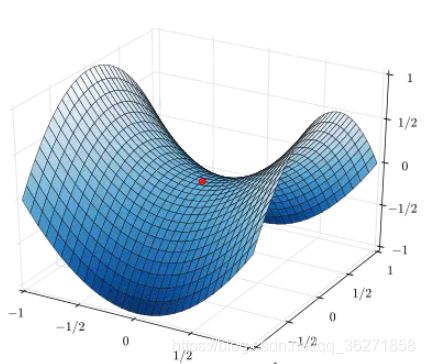
  同时，使用梯度下降更新权重时，对于每一个$w$，在计算$cost$和梯度的时候，需要对所有的样本进行计算并取均值，然后再更新权重$w$,这样做再计算规模很大的数据集时浪费大量的计算时间，而随机梯度下降则是对当前训练的每一个样本都计算梯度，随即更新权重$w$，由于每次用来计算梯度的样本都不是固定的，故名随机梯度下降(Stochastic Gradient Descent, SGD)。
  随机梯度下降与梯度下降的不同点

• 损失函数仅计算单个样本的损失
• 计算梯度时也仅计算单个样本的梯度

源代码

'''
随机梯度下降 SGD
'''

import numpy as np
import matplotlib.pyplot as plt

# dataSet
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 默认初始权重为1
w = 1

# learning rate
lr = 0.01

# define forwar function
def forward(x):
    return x * w

# define loss function
def loss(y_pred,y):
    # 此处仅计算了单个样本的误差
    return (y_pred - y) ** 2

# compute gradient
def gradient(x,y):
    # 在计算梯度时仅计算单个样本的梯度
    return 2 * x * (x * w - y)

print('Predict (before training)', 4, forward(4))

epoch_list = []
loss_list = []

# training
for epoch in range(100):
    # SGD在每一个样本计算梯度后都更新权重w
    for x_val, y_val in zip(x_data, y_data):
        grad = gradient(x_val, y_val)
        w = w - lr * grad
        y_pred= forward(x_val)
        loss_val = loss(y_pred, y_val)
        # print('\t')
    epoch_list.append(epoch)
    loss_list.append(loss_val)
    print('Epoch: ', epoch, 'w=%.3f' % w, 'loss=%.3f' %loss_val)

print('Predict (after training)', 4, '%.3f' %forward(4))
print('The linear model is y = x * %.2f' % w)

plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(epoch_list, loss_list)
plt.show()

结果

Predict (before training) 4 4
Predict (after training) 4 8.000
The linear model is y = x * 2.00

B站 刘二大人 PyTorch深度学习实践-线性模型