编辑距离,最长公共子序列,最长公共子串,最长递增子序列
1.编辑距离
编辑距离,又称Levenshtein距离(也叫做Edit Distance),是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。
例如将kitten一字转成sitting:
- sitten (k→s)
- sittin (e→i)
- sitting (→g)
最小编辑距离代码实例
 View Code
View Code
#include<iostream> #include<stdlib.h> #include<stdio.h> #include<string> using namespace std; #define maxNum 100 char a[maxNum],b[maxNum];//存放输入字符串 int c[maxNum][maxNum];//动态规划二维表 int diff(char a,char b)//判断字符a,b是否相等, 相等则编辑距离不增加,返回0,否则返回1 { if(a==b) return 0; else return 1; } int min(int a,int b,int c)//求三数中最小的 { int d; if(a<b) d=a; else d=b; if(c<d) return c; else return d; } int main() { printf("please input string a/n"); scanf("%s",a); printf("please input string b/n"); scanf("%s",b); printf("%s %s/n",a,b); int len_a=strlen(a); int len_b=strlen(b); int i,j; for(i=0;i<=len_a;i++) c[i][0]=i; for(j=0;j<=len_b;j++) c[0][j]=j; for(i=1;i<=len_a;i++) for(j=1;j<=len_b;j++) c[i][j]=min(1+c[i-1][j],1+c[i][j-1],diff(a[i-1],b[j-1])+c[i-1][j-1]); for(i=0;i<=len_a;i++) { for(j=0;j<=len_b;j++) cout<<c[i][j]<<" "; cout<<endl; } system("pause"); return 0; } /* please input string a EXPONENTIAL please input string b POLYNOMIAL EXPONENTIAL POLYNOMIAL 0 1 2 3 4 5 6 7 8 9 10 1 1 2 3 4 5 6 7 8 9 10 2 2 2 3 4 5 6 7 8 9 10 3 2 3 3 4 5 6 7 8 9 10 4 3 2 3 4 5 5 6 7 8 9 5 4 3 3 4 4 5 6 7 8 9 6 5 4 4 4 5 5 6 7 8 9 7 6 5 5 5 4 5 6 7 8 9 8 7 6 6 6 5 5 6 7 8 9 9 8 7 7 7 6 6 6 6 7 8 10 9 8 8 8 7 7 7 7 6 7 11 10 9 8 9 8 8 8 8 7 6 请按任意键继续. . . */
二维数组最后一个元素值就是最小编辑距离,也就是6.
2.最长公共子序列
2.1问题定义
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是,一个序列 S ,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。而最长公共子串(要求连续)和最长公共子序列是不同的,因为最长公共子序列不要求子序列在原有序列中连续出现。
2.2解题思路
这种题目使用动态规划解决。为了节约重复求相同子问题的时间,引入一个数组,不管它们是否对最终解有用,把所有子问题的解存于该数组中,这就是动态规划法所采用的基本方法。所以此处引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们首先进行自底向上的递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。具体思路如下
if(x[i]==y[j])//如果X[i] 和 Y[j]相等,那么c[i][j]的值可以通过1+c[i-1][j-1]得出。而c[i-1][j-1]已经推算出来。 c[i][j]=1+c[i-1][j-1] else{//如果X[i] 和 Y[j]不相等,那么x[i]和y[j]的最长公共子序列可能是x[i]与y[j-1]的最长公共子序列,也可能是x[i-1]与y[j]的最长公共子序列,我们求其最大值 c[i][j]=max(c[i][j-1],c[i-1][j]) }
我们上面的自底向上推算是在“c[i-1][j-1],c[i-1][j]与c[i][j-1]已经计算出来后再求c[i,j]”这个前提下进行的。所以我们构建c[][]这个数组是从头开始的。在创建好c[][]以后我们需要初始化这个二维数组,c[0][0...n]=0,c[0...m][0]=0。这是为了便于计算后面的c[1][1]使用。用于表示x[1]和y[1]的最长公共子序列,但是我们发现字符数组char* x[]跟char* y[]是从下标0开始计算的,所以在这里x[i][j]表示的是x[i-1]和y[j-1]的最长公共子序列。
最后问题可以用递归式写成:
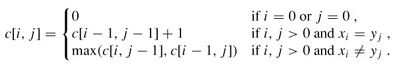
2.3最长公共子序列实例
 View Code
View Code
#include<iostream> #include<stdlib.h> #include<stdio.h> #include<string> using namespace std; #define maxNum 100 char a[maxNum],b[maxNum];//存放输入字符串 int c[maxNum][maxNum];//动态规划二维表 int max(int a,int b)//求三数中最大的 { if(a>b) return a; else return b; } int main() { printf("please input string a\n"); scanf("%s",a); printf("please input string b\n"); scanf("%s",b); printf("%s %s\n",a,b); int len_a=strlen(a); int len_b=strlen(b); int i,j; for(i=0;i<=len_a;i++) c[i][0]=0; for(j=0;j<=len_b;j++) c[0][j]=0; for(i=1;i<=len_a;i++) for(j=1;j<=len_b;j++) { if(a[i-1]==b[j-1]) { c[i][j]=c[i-1][j-1]+1; } else { c[i][j]=max(c[i-1][j],c[i][j-1]); } } for(i=0;i<=len_a;i++) { for(j=0;j<=len_b;j++) cout<<c[i][j]<<" "; cout<<endl; } system("pause"); return 0; } /* please input string a ABCBDAB please input string b BDCABA ABCBDAB BDCABA 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 2 2 0 1 1 2 2 2 2 0 1 1 2 2 3 3 0 1 2 2 2 3 3 0 1 2 2 3 3 4 0 1 2 2 3 4 4 */
根据上述解题思路给出代码实现
 View Code
View Code
//最长公共子序列,英文缩写为LCS(Longest Common Subsequence) #include<iostream> #include<stdlib.h> using namespace std; #define MaxLen 100 int max(int a,int b) { return a>b?a:b; } void LCSLength(char* s1, char* s2, int len1, int len2, int c[][MaxLen], int b[][MaxLen]) { int i,j; //初始化c[][] for(i=0;i<=len1;i++)//从0开始 { c[i][0]=0; } for(j=0;j<=len2;j++)//从0开始或者从1开始都可以 { c[0][j]=0; } for(i=1;i<=len1;i++)//从1开始 for(j=1;j<=len2;j++)//从1开始 { if(s1[i-1]==s2[j-1])//注意这里是i-1和j-1,因为字符串数组从下标0开始。 c[i][j]=c[i-1][j-1]+1; else c[i][j]=max(c[i][j-1],c[i-1][j]); } //输出c[][] for(i=0;i<=len1;i++) { for(j=0;j<=len2;j++) { cout<<c[i][j]<<" "; } cout<<endl; } } void PrintLCS() { } int main() { char* s1="ABCBDAB"; char* s2="BDCABA"; int len1=strlen(s1); int len2=strlen(s2); //cout<<len1<<endl; int c[MaxLen][MaxLen];//c[i][j]记录X[i]与Y[j] 的LCS 的长度 int b[MaxLen][MaxLen];//b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向 LCSLength(s1,s2,len1,len2,c,b); system("pause"); return 0; }
上述代码只给出了最长公共子序列的长度,但是没有输出最长公共子序列,如前所述我们需要通过一个b[][]来记录c[][]是由哪一步得到的。
- b[i][j]=0;//表示c[i][j]由c[i-1][j-1]+1得到
- b[i][j]=1;//表示c[i][j]由c[i][j-1]得到
- b[i][j]=-1;//表示c[i][j]由c[i-1][j]得到
这样在输出最长子序列的时候,我们从c[][]最后一个位置开始递归遍历。代码实现如下:
 View Code
View Code
//最长公共子序列,英文缩写为LCS(Longest Common Subsequence) #include<iostream> #include<stdlib.h> using namespace std; #define MaxLen 100 int max(int a,int b) { return a>b?a:b; } void LCSLength(char* s1, char* s2, int len1, int len2, int c[][MaxLen], int b[][MaxLen]) { int i,j; //初始化c[][] for(i=0;i<=len1;i++)//从0开始 { c[i][0]=0; } for(j=0;j<=len2;j++)//从0开始或者从1开始都可以 { c[0][j]=0; } for(i=1;i<=len1;i++)//从1开始 for(j=1;j<=len2;j++)//从1开始 { if(s1[i-1]==s2[j-1])//注意这里是i-1和j-1,因为字符串数组从下标0开始。 { c[i][j]=c[i-1][j-1]+1; b[i][j]=0;//表示c[i][j]由c[i-1][j-1]+1得到 } else if(c[i][j-1]>=c[i-1][j]) { c[i][j]=c[i][j-1]; b[i][j]=1;//表示c[i][j]由c[i][j-1]得到 } else { c[i][j]=c[i-1][j]; b[i][j]=-1;//表示c[i][j]由c[i-1][j]得到 } } ////输出c[][] //for(i=0;i<=len1;i++) //{ // for(j=0;j<=len2;j++) // { // cout<<c[i][j]<<" "; // } // cout<<endl; //} } void PrintLCS(char* s1,int i,int j,int b[][MaxLen]) { //递归退出条件 if(i<=0||j<=0) return; if(b[i][j]==0) { PrintLCS(s1,i-1,j-1,b); cout<<s1[i-1]; } else if(b[i][j]==1)//表示c[i][j]由c[i][j-1]得到 { PrintLCS(s1,i,j-1,b); } else { PrintLCS(s1,i-1,j,b); } } int main() { char* s1="ABCBDAB"; char* s2="BDCABA"; int len1=strlen(s1); int len2=strlen(s2); //cout<<len1<<endl; int c[MaxLen][MaxLen];//c[i][j]记录X[i]与Y[j] 的LCS 的长度 int b[MaxLen][MaxLen];//b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向 LCSLength(s1,s2,len1,len2,c,b); PrintLCS(s1,len1,len2,b); system("pause"); return 0; }
3.最长公共子串
3.1解体思路
找两个字符串的最长公共子串,这个子串要求在原字符串中是连续的。可以用动态规划来求解。我们采用一个二维矩阵来记录中间的结果。这个二维矩阵怎么构造呢?首先初始化这个二维数组c[][],
- 如果x[0..i]=y[0],则c[i][0]=1,否则c[i][0]=0
- 如果y[0..j]=x[0],则c[0][j]=1,否则c[0][j]=0
然后计算c[i][j]的值,如果x[i]==y[j],则c[i][j]=c[i-1][j-1]+1。
直接举个例子吧:"ABCBDAB"和"BDCABA"(当然我们现在一眼就可以看出来最长公共子串是"AB"或"BD")
B D C A B A A 0 0 0 1 0 1 B 1 0 0 0 2 0 C 0 0 1 0 0 0 B 1 0 0 0 1 0 D 0 2 0 0 0 0 A 0 0 0 1 0 1 B 1 0 0 0 2 0
3.2代码实现
 View Code
View Code
//最长公共子串,英文缩写为LCS(Longest Common Substring) #include<iostream> #include<stdlib.h> using namespace std; #define MaxLen 100 void LCSubstring(char* s1, char* s2, int len1, int len2, int c[][MaxLen]) { int i,j; //初始化c[][] for(i=0;i<len1;i++) { if(s1[i]==s2[0]) c[i][0]=1; else c[i][0]=0; } for(j=0;j<len2;j++) { if(s2[j]==s1[0]) c[0][j]=1; else c[0][j]=0; } int max=0; int m,n; for(i=1;i<len1;i++)//从1开始 for(j=1;j<len2;j++)//从1开始 { if(s1[i]==s2[j]) { c[i][j]=c[i-1][j-1]+1; if(c[i][j]>max)//记录最长公共字串的位置 { max=c[i][j]; m=i; n=j; } } else { c[i][j]=0; } } for(i=m-max+1;i<=m;i++)//输出公共字串 { cout<<s1[i]; } cout<<endl; //输出c[][] for(i=0;i<len1;i++) { for(j=0;j<len2;j++) { cout<<c[i][j]<<" "; } cout<<endl; } } int main() { char* s1="ABCBDAB"; char* s2="BDCABA"; int len1=strlen(s1); int len2=strlen(s2); int c[MaxLen][MaxLen];//c[i][j]记录X[i]与Y[j] 的LCS 的长度 LCSubstring(s1,s2,len1,len2,c); system("pause"); return 0; }
4.最长递增子序列
4.1参考文献:
http://blog.csdn.net/hhygcy/article/details/3950158
4.2解题思路
既然已经说到了最长公共子序列,就把这个递增子序列也说了。同样的,这里subsequence表明了这样的子序列不要求是连续的。比如说有子序列{1, 9, 3, 8, 11, 4, 5, 6, 4, 19, 7, 1, 7 },这样一个字符串的的最长递增子序列就是{1,3,4,5,6,7}或者{1,3,4,5,6,19}。
其实这个问题和前面的最长公共子序列问题还是有一定的关联的。
- 假设我们的初始的序列 S1= {1, 9, 3, 8, 11, 4, 5, 6, 4, 19, 7, 1, 7 }。
- 那我们从小到大先排序一下。得到了S1'={1, 1, 3, 4, 4, 5, 6, 7, 7 , 8, 9, 11, 19}。
这样我们再求S1和S1'的最长公共子序列就是S1的最长递增子序列了。这个过程还是比较直观的。但是这个不是这次要说的重点,这个问题有比较传统的做法的.
我们定义L(j)是一个优化的子结构,也就是最长递增子序列。那么L(j)和L(1..j-1)的关系可以描述成
L(j) = max {L(i), i<j && Ai<Aj } + 1; 也就是说L(j)等于之前所有的L(i)中最大的的L(i)加一。这样的L(i)需要满足的条件就是Ai<Aj。这个推断还是比较容易理解的。就是选择j之前所有的满足小于当前数组的最大值。
最后求max(L(j))就是最长递增子序列,需要注意的是L[len-1]并不一定是最长递增子序列的长度。
4.3代码实现
 View Code
View Code
#include<iostream> #include<stdlib.h> using namespace std; #define MaxLen 100 //方法1:通过求有向无环图的最长路径来求最长递增子序列,通过二维数组构建有向无环图。 int LIS(int arry[],int len,int e[][MaxLen],int L[]) { int i,j; //初始化有向图 for(i=0;i<len;i++) { L[i]=1;//初始化L[] for(j=i+1;j<len;j++) { if(arry[i]<arry[j]) e[i][j]=1; else e[i][j]=0; } } //转换为求有向图的最长路径 for(i=0;i<len;i++) { for(j=i+1;j<len;j++) { if(e[i][j]==1&&L[j]<1+L[i]) { L[j]=1+L[i]; } } } int max=0; //根据L[i]求最长递增子序列 for(int i=0;i<len;i++) if(L[i]>max) max=L[i]; return max;//L[len-1]不一定就最长递增子序列的长度 } //方法2: int LIS2(int arry[],int len,int L[]) { int i,j; for(i=0;i<len;i++) { L[i]=1;//初始化L[] } for(i=1;i<len;i++) { for(int j=i+1;j<len;j++) { if(arry[i]<arry[j]&&L[j]<1+L[i]) L[j]=1+L[i]; } } int max=0; //根据L[i]求最长递增子序列 for(int i=0;i<len;i++) if(L[i]>max) max=L[i]; return max;//L[len-1]不一定就最长递增子序列的长度 } //打印最长递增子序列 void printString(int p[],int k,int arry[]) { if(p[k]==-1) return; printString(p,p[k],arry); cout<<arry[k]; } //方法3: int LIS3(int arry[],int len,int L[]) { int p[MaxLen]; int i,j; for(i=0;i<len;i++) { L[i]=1;//初始化L[] p[i]=-1; } for(i=1;i<len;i++) { for(int j=i+1;j<len;j++) { if(arry[i]<arry[j]&&L[j]<1+L[i]) { L[j]=1+L[i]; p[j]=i;//表示arry[j]的前一个元素使arry[i]。 } } } int max=0; int k; //根据L[i]求最长递增子序列 for(int i=0;i<len;i++) { if(L[i]>max) { max=L[i]; k=i; } } printString(p,k,arry); cout<<endl; return max;//L[len-1]不一定就最长递增子序列的长度 } void main() { int arry[]={5,2,8,6,3,6,9,7}; int len=sizeof(arry)/sizeof(int); int e[MaxLen][MaxLen]; int *L=new int[len]; cout<<LIS(arry,len,e,L)<<endl; cout<<LIS2(arry,len,L)<<endl; cout<<LIS3(arry,len,L)<<endl; system("pause"); }
但是上面的 LIS和 LIS2两种实现都没有给出递增子序列本身,只给出了长度。而 LIS3能够输出一个子序列。举例说明其实现方式:
arry[]={5,2,8,9,3}
L[0...i] p[0...i]
1, 1, 1, 1, 1 -1, -1, -1, -1, -1
2, 2 0, 0
2 1
3 2
如上述所示,我们首先初始化数组L[]和p[],其中L用于记录递增子序列的长度,而p[]用于回溯递增子序列,其中p[j]=i表示arry[i]->arry[j]是一个递增子序列。我们在L[]中能够求出递增子序列的长度max以及递增子序列的末尾元素所在位置k。然后通过k我们回溯数组p,因此这里使用了递归方式打印递增子序列。
