均值-方差模型实现及应用_python_数据分析_9

用的是米筐的研究模块，从结果来看，均值方差模型对参数的敏感性很高，很多参数都不如随机权重，很难应用到实战。

import pandas as pd
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt

stockslist = ['000001.XSHE','000002.XSHE','600004.XSHG','600033.XSHG','000651.XSHE']
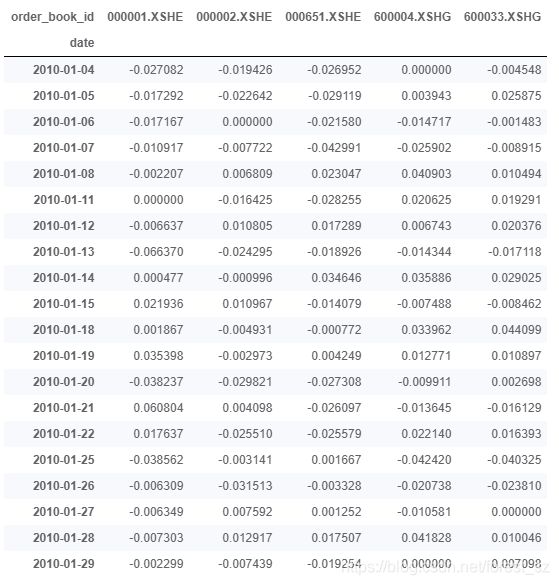
data = get_price_change_rate(stockslist,start_date = '20100101',end_date = '20200420')
data.to_csv('MeanVar.csv')
print(data.head(20))
train_set = data[data.index<'20171231']
#print(train_set.tail(20))
test_set = data[data.index>'20180101']
#print(test_set.head(20))

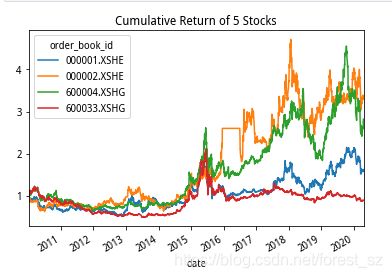
#看一下5个股票的历史表现
cumreturn = (1 + data).cumprod()
cumreturn.plot()
plt.title('Cumulative Return of Stocks')
plt.show()

#相关性分析
data.corr()

#核心模块，实现均值方差模型的计算
class MeanVariance:
    #传入收益率数据
    def __init__(self,returns):
        self.returns = returns
    #定义最小化方差函数，即求解二次规划
    def minVar(self,goalRet):
        covs = np.array(self.returns.cov())
        means = np.array(self.returns.mean())
        L1 = np.append(np.append(covs.swapaxes(0,1),[means],0),
                      [np.ones(len(means))],0).swapaxes(0,1)
        L2 = list(np.ones(len(means)))
        L2.extend([0,0])
        L3 = list(means)
        L3.extend([0,0])
        L4 = np.array([L2,L3])
        L = np.append(L1,L4,0)
        results = linalg.solve(L,np.append(np.zeros(len(means)),[1,goalRet],0))
        return np.array([list(self.returns.columns),results[:-2]])
    #定义绘制最小方差前缘曲线函数
    def frontierCurve(self):
        goals = [x/500000 for x in range(-100,4000)]
        variances = list(map(lambda x: self.calVar(self.minVar(x)[1,:].astype(np.float)),goals))
        plt.plot(variances,goals)
    #定义各资产比例，计算收益率均值
    def meanRet(self,fracs):
        meanRisky = ffn.to_returns(self.returns).mean()
        #assert (len(meanRisky == len(fracs),'Length of fractions must be equal to number of assets')
        return np.sum(np.multiply(meanRisky,np.array(fracs)))
    #定义各资产比例，计算收益率方差
    def calVar(self,fracs):
        return np.dot(np.dot(fracs,self.returns.cov()),fracs)

#计算有效前缘
minVar = MeanVariance(data)
minVar.frontierCurve()

#计算训练集权重
varMinimizer = MeanVariance(train_set)
goal_return = 0.003
portfolio_weight = varMinimizer.minVar(goal_return)
portfolio_weight

#计算测试集收益率
test_return = np.dot(test_set,np.array([portfolio_weight[1,:].astype(np.float)]).swapaxes(0,1))
test_return = pd.DataFrame(test_return,index = test_set.index)
test_cum_return = (1+test_return).cumprod()

#计算随机权重组合
sim_weight = np.random.uniform(0,1,(100,len(stockslist)))
sim_weight = np.apply_along_axis(lambda x: x/sum(x),1,sim_weight)
sim_return = np.dot(test_set,sim_weight.swapaxes(0,1))
sim_return = pd.DataFrame(sim_return,index = test_cum_return.index)
sim_cum_return = (1+sim_return).cumprod()

plt.plot(sim_cum_return.index,sim_cum_return,color = 'green')
plt.plot(test_cum_return.index,test_cum_return,label = 'MeanVar')
plt.legend()
plt.title('MeanVar & Random')