研报复现系列(二):【光大证券】基于阻力支撑相对强度(RSRS)的市场择时
1.研报概述
本文是券商金工研报复现系列的第二篇,文本复现了【光大证券】的【基于阻力支撑相对强度(RSRS)的市场择时】。
阻力位与支撑位传统的应用方法一般是选取特定的阻力位、支撑位作为阈值来进行突破、反转策略的构建,常见的策略如均线策略:【若当日收盘价超过 20 日均线,则建仓买入。一直持仓至收盘价低于 20 日均线,卖出平仓】。
不同于选取阻力位与支撑位阈值区间的传统应用方法,该篇研报关注阻力位与支撑位的相对强弱程度。
阻力位与支撑位实际上反应了交易者对市场状态顶部和底部的预期判断。
从直觉上看,如果这种预期判断极易改变,则表明支撑位或阻力位的强度小,有效性弱;而如果众多交易者预期较为一致、变动不大,则表明支撑位或阻力位强度高,有效性强。
如果支撑位的强度小,作用弱于阻力位,则表明市场参与者对于支撑位的分歧大于对于阻力位的分歧,市场接下来更倾向于向熊市转变。而如果支撑位的强度大,作用强于阻力位,则表示市场参与者对于支撑位的认可度更高于对于阻力位的认可度,市场更倾向于在牛市转变。
我们按照不同市场状态分类来说明支撑阻力相对强度的应用逻辑:
1.市场在上涨牛市中:
如果支撑明显强于阻力,牛市持续,价格加速上涨
如果阻力明显强于支撑,牛市可能即将结束,价格见顶
2.市场在震荡中:
如果支撑明显强于阻力,牛市可能即将启动
如果阻力明显强于支撑,熊市可能即将启动
3.市场在下跌熊市中:
如果支撑明显强于阻力,熊市可能即将结束,价格见底
如果阻力明显强于支撑,熊市持续,价格加速下跌
该篇研报构建衡量阻力位与支撑位相对强度的指标RSRS(Resistance Support Relative Strength),当支撑位强度小,阻力位强度大时,RSRS的值较高,相反RSRS的值较低。
2.研究环境
数据源:聚宽JoinQuant,2005.6-2017.5日线数据
import datetime
import math
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
import warnings
warnings.filterwarnings("ignore")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
3.研报复现
3.1量化阻力位支撑位相对强度RSRS
该研报要解决的首要问题是如何定义并量化阻力位与支撑位的相对强度,而解决该问题首先要选取一对合适的阻力位与支撑位指标。
3.1.1如何选取阻力位与支撑位
量化阻力位与支撑位相对强度的第一步,是选取合适的阻力位和支撑位指标。在技术分析学派中,已经有了许多对于支撑位与阻力位的定义,常见的包括通道线(布林带的上下轨),一段时间内 的前高与前低,区间震荡线(DPO)等等。
该篇研报选取每日的最高价和最低价作为阻力位和支撑位,因为每日的最高价和最低价可以迅速反应近期市场对于阻力位与支撑位态度的性质。
3.1.2RSRS构建的基本思想
本篇研报提出了多种相对强弱程度的量化方法,并且是逐层优化的关系。
这里对各自方法进行简单的介绍,后面会给出每种量化方法构建的策略的效果。
基本思想:
这里使用最高价和最低价的相对变化速率,即类似 delta(high)/delta(low)的值来描
述支撑位与阻力位的相对强度,即最低价每变动 1 的时候,最高价变动的幅度。
基于该基本思想,原研报使用
线性回归线的斜率
斜率标准分
修正标准分
右偏标准分
四种方法量化阻力支撑相对强弱程度。这四种方法是逐层递进、优化的关系。
最后又结合价量数据优化策略。本文将会对每一种方法给出其计算方法和构建的策略的效果。
3.2 具体计算方法和策略效果
3.2.0 数据格式与策略统计函数
在给出具体的策略代码之前,我们先介绍策略使用的数据格式。
在策略回测中,我们使用DataFrame格式的数据df。其不仅包含价格和RSRS指标的时间序列,还有flag和position两列。
flag是开仓平仓标志位,df[‘flag’][i]为1时,表明第i日进行了开仓操作,df[‘flag’][i]为-1时,表明第i日进行了平仓操作。position是账户持仓标志位,其值为1表明当前账户持有证券,其值为0表明当前账户为空仓。
同时,本文构建的策略中,只有当前账户空仓时才进行买入操作。
这里,我们先给出统计策略结果的函数,后文会多次用到该函数。
def calculate_statistics(df):
'''
输入:
DataFrame类型,包含价格数据和仓位、开平仓标志
position列:仓位标志位,0表示空仓,1表示持有标的
flag列:买入卖出标志位,1表示在该时刻买入,-1表示在该时刻卖出
close列:日收盘价
输出:dict类型,包含夏普比率、最大回撤等策略结果的统计数据
'''
#净值序列
df['net_asset_pct_chg'] = df.net_asset_value.pct_change(1).fillna(0)
#总收益率与年化收益率
total_return = (df['net_asset_value'][df.shape[0]-1] -1)
annual_return = (total_return)**(1/(df.shape[0]/252)) -1
total_return = total_return*100
annual_return = annual_return*100
#夏普比率
df['ex_pct_chg'] = df['net_asset_pct_chg']
sharp_ratio = df['ex_pct_chg'].mean() * math.sqrt(252)/df['ex_pct_chg'].std()
#回撤
df['high_level'] = (
df['net_asset_value'].rolling(
min_periods=1, window=len(df), center=False).max()
)
df['draw_down'] = df['net_asset_value'] - df['high_level']
df['draw_down_percent'] = df["draw_down"] / df["high_level"] * 100
max_draw_down = df["draw_down"].min()
max_draw_percent = df["draw_down_percent"].min()
#持仓总天数
hold_days = df['position'].sum()
#交易次数
trade_count = df[df['flag']!=0].shape[0]/2
#平均持仓天数
avg_hold_days = int(hold_days/trade_count)
#获利天数
profit_days = df[df['net_asset_pct_chg'] > 0].shape[0]
#亏损天数
loss_days = df[df['net_asset_pct_chg'] < 0].shape[0]
#胜率(按天)
winrate_by_day = profit_days/(profit_days+loss_days)*100
#平均盈利率(按天)
avg_profit_rate_day = df[df['net_asset_pct_chg'] > 0]['net_asset_pct_chg'].mean()*100
#平均亏损率(按天)
avg_loss_rate_day = df[df['net_asset_pct_chg'] < 0]['net_asset_pct_chg'].mean()*100
#平均盈亏比(按天)
avg_profit_loss_ratio_day = avg_profit_rate_day/abs(avg_loss_rate_day)
#每一次交易情况
buy_trades = df[df['flag']==1].reset_index()
sell_trades = df[df['flag']==-1].reset_index()
result_by_trade = {
'buy':buy_trades['close'],
'sell':sell_trades['close'],
'pct_chg':(sell_trades['close']-buy_trades['close'])/buy_trades['close']
}
result_by_trade = pd.DataFrame(result_by_trade)
#盈利次数
profit_trades = result_by_trade[result_by_trade['pct_chg']>0].shape[0]
#亏损次数
loss_trades = result_by_trade[result_by_trade['pct_chg']<0].shape[0]
#单次最大盈利
max_profit_trade = result_by_trade['pct_chg'].max()*100
#单次最大亏损
max_loss_trade = result_by_trade['pct_chg'].min()*100
#胜率(按次)
winrate_by_trade = profit_trades/(profit_trades+loss_trades)*100
#平均盈利率(按次)
avg_profit_rate_trade = result_by_trade[result_by_trade['pct_chg'] > 0]['pct_chg'].mean()*100
#平均亏损率(按次)
avg_loss_rate_trade = result_by_trade[result_by_trade['pct_chg'] < 0]['pct_chg'].mean()*100
#平均盈亏比(按次)
avg_profit_loss_ratio_trade = avg_profit_rate_trade/abs(avg_loss_rate_trade)
statistics_result = {
'net_asset_value':df['net_asset_value'][df.shape[0]-1],#最终净值
'total_return':total_return,#收益率
'annual_return':annual_return,#年化收益率
'sharp_ratio':sharp_ratio,#夏普比率
'max_draw_percent':max_draw_percent,#最大回撤
'hold_days':hold_days,#持仓天数
'trade_count':trade_count,#交易次数
'avg_hold_days':avg_hold_days,#平均持仓天数
'profit_days':profit_days,#盈利天数
'loss_days':loss_days,#亏损天数
'winrate_by_day':winrate_by_day,#胜率(按天)
'avg_profit_rate_day':avg_profit_rate_day,#平均盈利率(按天)
'avg_loss_rate_day':avg_loss_rate_day,#平均亏损率(按天)
'avg_profit_loss_ratio_day':avg_profit_loss_ratio_day,#平均盈亏比(按天)
'profit_trades':profit_trades,#盈利次数
'loss_trades':loss_trades,#亏损次数
'max_profit_trade':max_profit_trade,#单次最大盈利
'max_loss_trade':max_loss_trade,#单次最大亏损
'winrate_by_trade':winrate_by_trade,#胜率(按次)
'avg_profit_rate_trade':avg_profit_rate_trade,#平均盈利率(按次)
'avg_loss_rate_trade':avg_loss_rate_trade,#平均亏损率(按次)
'avg_profit_loss_ratio_trade':avg_profit_loss_ratio_trade#平均盈亏比(按次)
}
return statistics_result
3.2.1斜率方法
因为市场上存在噪声,所以考虑用连续N日的最高价与最低价的线性回归模型的斜率来量化支撑位与阻力位的相对强度,以求增加信噪比。
即,取连续N日的最高价与最低价的线性回归模型
high = alpha + beta*low
中的beta,即直线的斜率,作为我们的相对强度RSRS。
斜率指标计算方法:
- 取前 N 日的最高价序列与最低价序列。
- 将两列数据按式(1)的模型进行 OLS 线性回归。
- 将拟合后的 beta 值作为当日 RSRS 斜率指标值。
在原研报中,经过对N的不同取值的比较,N取18时,量化出的指标构建的策略更有效。
基于斜率方法,构建策略:
- 计算 RSRS 斜率。
- 如果斜率大于 1,则买入持有。
- 如果斜率小于 0.8,则卖出手中持股平仓。
策略源代码
#当日斜率指标计算方式,线性回归
def cal_nbeta(df,n):
nbeta = []
trade_days = len(df.index)
df['position'] = 0
df['flag'] = 0
position = 0
#计算斜率值
for i in range(trade_days):
if i < (n-1):
#n-1为配合接下来用iloc索引
continue
else:
x = df['low'].iloc[i-n+1:i+1]
#iloc左闭右开
x = sm.add_constant(x)
y = df['high'].iloc[i-n+1:i+1]
regr = sm.OLS(y,x)
res = regr.fit()
beta = round(res.params[1],2)#斜率指标
nbeta.append(beta)
df1 = df.iloc[n-1:]
df1['beta'] = nbeta
#执行交易策略
for i in range(len(df1.index)-1):
#此处-1是为了避免最后一行
if df1['beta'].iloc[i] > 1 and position == 0:
df1['flag'].iloc[i] = 1 #开仓标志
df1['position'].iloc[i+1] =1 #仓位不为空
position = 1
elif df1['beta'].iloc[i] < 0.8 and position == 1:
df1['flag'].iloc[i] = -1 #平仓标志
df1['position'].iloc[i+1] = 0 #仓位为空
position = 0
else:
df1['position'].iloc[i+1] = df1['position'].iloc[i]
#计算净值序列
df1['net_asset_value'] = (1+df1.close.pct_change(1).fillna(0)*df1.position).cumprod()
return df1
策略净值曲线
策略的统计指标
| 统计量 | 斜率策略 |
|---|---|
| 净值 | 10.66 |
| 收益率 | 965.73% |
| 年化收益率 | 21.92% |
| 夏普比率 | 1.16 |
| 最大回撤 | -50.26% |
| 持仓天数 | 1184 |
| 交易次数 | 21 |
| 平均持仓天数 | 56 |
| 盈利天数 | 747 |
| 亏损天数 | 575 |
| 胜率(按天) | 56.51% |
| 平均盈利率(按天) | 1.31% |
| 平均亏损率(按天) | -1.25% |
| 平均盈亏比(按天) | 1.05 |
| 盈利次数 | 16 |
| 亏损次数 | 5 |
| 单次最大盈利 | 170% |
| 单次最大亏损 | -12% |
| 胜率(按次) | 76.19% |
| 平均盈利率(按次) | 25% |
| 平均亏损率(按次) | -3% |
| 平均盈亏比(按次) | 7.86 |
3.2.2斜率方法的优化——斜率标准分
使用斜率指标构建策略时,需要参考斜率指标在历史上的均值和标准差以选择合适的开仓、平仓阈值。
但随时市场的变化,不同时期数据的均值与标准差可能会发生变化。同时交易者也可能更关心在当前市场在近期的环境中处在什么样的位置,或者接下来一段时间市场相比于目前将会有怎么的发展。所以相较于直接使用斜率在整个历史上的均值和标准差来帮助选择阈值,根据斜率在最近一定周期内(600个交易日)的标准分确定阈值可以更加灵活地适应近期的整体市场基本状态。
斜率标准分计算方法:
- 取前 M 日的斜率时间序列。
- 以此样本计算当日斜率的标准分。
- 将计算得到的标准分 z 作为当日 RSRS 标准分指标值。
构建标准分策略:
1.根据斜率计算标准分(参数 N=18,M=600)。
2.如果标准分大于 S(参数 S=0.7),则买入持有。
3.如果标准分小于-S,则卖出平仓。
策略源代码
#标准分策略
def cal_stdbeta(df,n):
df['position'] = 0
df['flag'] = 0
position = 0
df1 = cal_nbeta(df,n)
pre_stdbeta = df1['beta']
pre_stdbeta = np.array(pre_stdbeta)
#转化为数组,可以对整个数组进行操作
sigma = np.std(pre_stdbeta)
mu = np.mean(pre_stdbeta)
#标准化
stdbeta = (pre_stdbeta-mu)/sigma
df1['stdbeta'] = stdbeta
for i in range(len(df1.index)-1):
#此处-1是为了避免最后一行
if df1['stdbeta'].iloc[i] > 0.7 and position == 0:
df1['flag'].iloc[i] = 1
df1['position'].iloc[i+1] =1
position = 1
elif df1['stdbeta'].iloc[i] < -0.7 and position == 1:
df1['flag'].iloc[i] = -1
df1['position'].iloc[i+1] = 0
position = 0
else:
df1['position'].iloc[i+1] = df1['position'].iloc[i]
df1['net_asset_value'] = (1+df1.close.pct_change(1).fillna(0)*df1.position).cumprod()
return df1
#stdbeta是数组 beta是列表
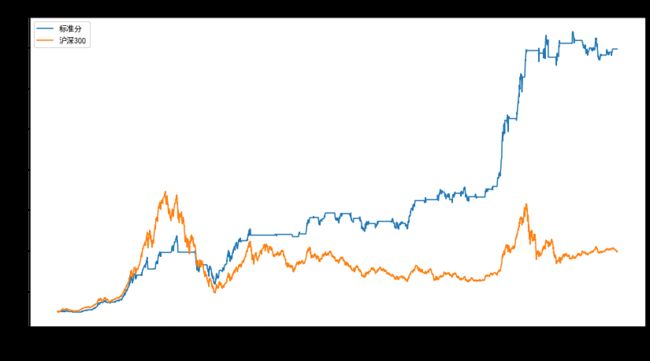
净值曲线图
策略的统计指标
| 统计量 | 标准分策略 |
|---|---|
| 净值 | 13.93 |
| 收益率 | 1292.70% |
| 年化收益率 | 25.07% |
| 夏普比率 | 1.28 |
| 最大回撤 | -50.26% |
| 持仓天数 | 1298 |
| 交易次数 | 67 |
| 平均持仓天数 | 19 |
| 盈利天数 | 741 |
| 亏损天数 | 557 |
| 胜率(按天) | 57.09% |
| 平均盈利率(按天) | 1.32% |
| 平均亏损率(按天) | -1.25% |
| 平均盈亏比(按天) | 1.06 |
| 盈利次数 | 40 |
| 亏损次数 | 26 |
| 单次最大盈利 | 91% |
| 单次最大亏损 | -41% |
| 胜率(按次) | 60.61% |
| 平均盈利率(按次) | 18% |
| 平均亏损率(按次) | -9% |
| 平均盈亏比(按次) | 2.05 |
3.2.3再优化——修正标准分:考虑到线性拟合的程度
使用线性回归拟合直线的斜率或其标准分作为相对强弱程度时,可能出现斜率或标准分的绝对值很大,但直线本身的拟合效果并不好,使得斜率或斜率的标准分本身不能很好的体现出相对强弱程度的问题。需要构建相对强弱程度指标时可以考虑到线性模型拟合结果的好坏。
在线性回归中,R 平方值(决定系数)可以理解成线性拟合效果的程度。
因此,使用
修正标准分=标准分*R 平方值(决定系数)
来量化相对强弱程度,可以削弱直线拟合效果对指标效果的影响。
构建修正标准分策略
- 计算修正标准分(N=16,M=300)。
- 如果修正标准分大于 S(S=0.7),则买入持有。
- 如果修正标准分小于-S,则卖出平仓。
策略源代码
#RSRS 标准分指标优化,修正标准分
def cal_better_stdbeta(df,n):
nbeta = []
R2 = []
trade_days = len(df.index)
for i in range(trade_days):
if i < (n-1):
#n-1为配合接下来用iloc索引
continue
else:
x = df['low'].iloc[i-n+1:i+1]
#iloc左闭右开
x = sm.add_constant(x)
y = df['high'].iloc[i-n+1:i+1]
regr = sm.OLS(y,x)
res = regr.fit()
beta = round(res.params[1],2)
R2.append(res.rsquared)
nbeta.append(beta)
prebeta = np.array(nbeta)
sigma = np.std(prebeta)
mu = np.mean(prebeta)
stdbeta = (prebeta-mu)/sigma
r2 = np.array(R2)
better_stdbeta = r2*stdbeta#修正标准分
df1 = df.iloc[n-1:]
df1['beta'] = nbeta
df1['flag'] = 0
df1['position'] = 0
position = 0
df1['better_stdbeta'] = better_stdbeta
for i in range(len(df1.index)-1):
#此处-1是为了避免最后一行
if df1['better_stdbeta'].iloc[i] > 0.7 and position == 0:
df1['flag'].iloc[i] = 1
df1['position'].iloc[i+1] =1
position = 1
elif df1['better_stdbeta'].iloc[i] < -0.7 and position == 1:
df1['flag'].iloc[i] = -1
df1['position'].iloc[i+1] = 0
position = 0
else:
df1['position'].iloc[i+1] = df1['position'].iloc[i]
df1['net_asset_value'] = (1+df1.close.pct_change(1).fillna(0)*df1.position).cumprod()
return df1
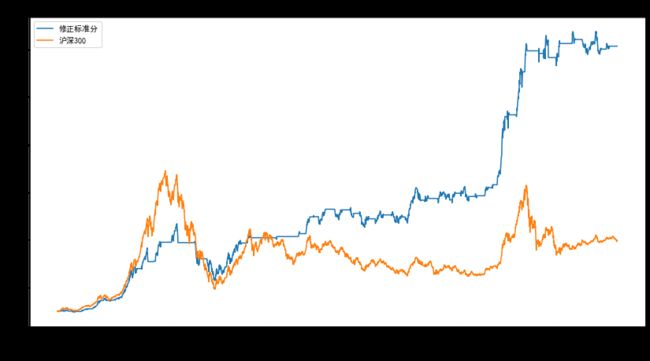
策略指标
| 量 | 修正标准分策略 |
|---|---|
| 净值 | 12.15 |
| 收益率 | 1115.40% |
| 年化收益率 | 23.47% |
| 夏普比率 | 1.19 |
| 最大回撤 | -51.28% |
| 持仓天数 | 1397 |
| 交易次数 | 46 |
| 平均持仓天数 | 30 |
| 盈利天数 | 790 |
| 亏损天数 | 607 |
| 胜率(按天) | 56.55% |
| 平均盈利率(按天) | 1.30% |
| 平均亏损率(按天) | -1.25% |
| 平均盈亏比(按天) | 1.05 |
| 盈利次数 | 32 |
| 亏损次数 | 14 |
| 单次最大盈利 | 76% |
| 单次最大亏损 | -18% |
| 胜率(按次) | 69.57% |
| 平均盈利率(按次) | 11% |
| 平均亏损率(按次) | -3% |
| 平均盈亏比(按次) | 3.3 |
3.2.4再再优化——右偏标准分:在实践过程中的猜想
原研报在分析比较标准分和修正标准分对后市的相关性时,发现右侧(即z>0)的标准分对后市收益有较好的预测性,而左侧的标准分则失去了预测性,因为左侧的标准分占了整体的大部分,所以整体标准分与后市收益相关性较低。而修正标准分右侧的取值范围扩大了(相对于左侧而言,并非绝对的值域),修正标准分整体上呈现了更好的预测性。
因此猜测:是否右侧的取值范围越广(相对于左侧而言,并非绝对的值域范围),指标的预测性更好?
为了验证该猜想,构建右偏标准分
右偏标准分=修正标准分*斜率
构建右偏标准分策略
- 计算右偏标准分(N=16,M=300)。
- 如果右偏标准分大于 S(S=0.7),则买入持有。
- 如果右偏标准分小于-S,则卖出平仓。
策略源代码
#右偏标准分 此时N取16
def cal_right_stdbeta(df,n):
df1 = cal_better_stdbeta(df,n)
df1['position'] = 0
df1['flag'] = 0
df1['net_value'] = 0
position = 0
df1['right_stdbeta'] = df1['better_stdbeta']*df1['beta']
#修正标准分与斜率值相乘能够达到使原有分布右偏的效果
for i in range(len(df1.index)-1):
#此处-1是为了避免最后一行
if df1['right_stdbeta'].iloc[i] > 0.7 and position == 0:
df1['flag'].iloc[i] = 1
df1['position'].iloc[i+1] =1
position = 1
elif df1['right_stdbeta'].iloc[i] < -0.7 and position == 1:
df1['flag'].iloc[i] = -1
df1['position'].iloc[i+1] = 0
position = 0
else:
df1['position'].iloc[i+1] = df1['position'].iloc[i]
df1['net_asset_value'] = (1+df1.close.pct_change(1).fillna(0)*df1.position).cumprod()
return df1
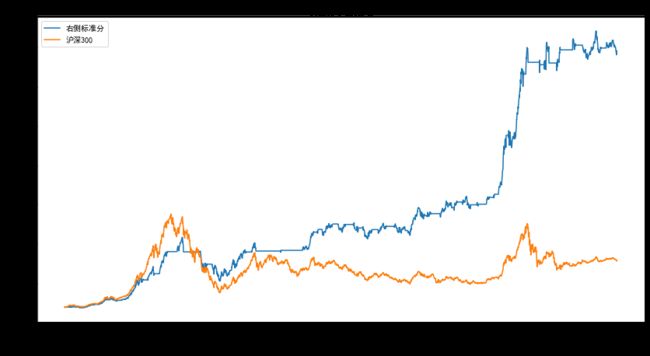
策略指标
| 统计量 | 右偏标准分 |
|---|---|
| 净值 | 17.67 |
| 收益率 | 1667.22% |
| 年化收益率 | 27.88% |
| 夏普比率 | 1.29 |
| 最大回撤 | -51.16% |
| 持仓天数 | 1638 |
| 交易次数 | 37.5 |
| 平均持仓天数 | 43 |
| 盈利天数 | 928 |
| 亏损天数 | 710 |
| 胜率(按天) | 56.65% |
| 平均盈利率(按天) | 1.27% |
| 平均亏损率(按天) | -1.22% |
| 平均盈亏比(按天) | 1.04 |
| 盈利次数 | 26 |
| 亏损次数 | 11 |
| 单次最大盈利 | 91% |
| 单次最大亏损 | -17% |
| 胜率(按次) | 70.27% |
| 平均盈利率(按次) | 15% |
| 平均亏损率(按次) | -3% |
| 平均盈亏比(按次) | 4.6 |
3.3 结合市场状态的优化
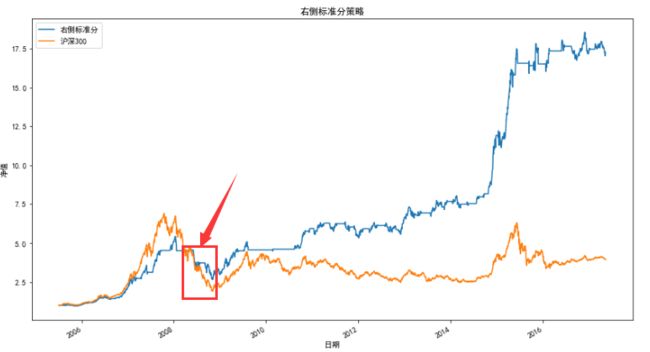
基于上文介绍的四种阻力支撑相对强弱程度指标RSRS构建出的交易策略都大幅度地跑赢了基准收益,但也都有一个共同的缺陷:净值在08年股灾期间都出现了大幅的回撤。
这是因为按照阻力支撑相对强弱指标的逻辑,策略大概率是在左侧开仓、左侧平仓。(这里的左侧是指股价呈现“V”字型时的下跌阶段,并不是上文讨论右偏标准分时提到的左侧)。但当市场处在大熊市状态时,如果开仓预测失误,就会造成严重的亏损。
因此,我们期望在保证收益的同时,尽可能降低熊市错误开仓的几率。
简单的想法是:先判断市场状态是处在上升还是下跌趋势,再结合RSRS构建买入、卖出策略。
3.3.1 结合均线指标的优化
有很多指标帮助我们判断近期市场状态,如MA,MACD等。在这里我们使用当日 20 日均线值与 3 日前 20 日均线值的相对大小来判断近期市场状态。
优化后的交易策略为:
1.计算 RSRS 标准分指标买卖信号。
- 如果指标发出买入信号,同时满足前一日 MA(20)的值大于前三日MA(20)的值,则买入。
- 如果指标发出卖出信号,则卖出手中持股。
策略代码
RSRS 指标配合价格数据优化策略
def cal_ma_beta(df,n):
df1 = cal_stdbeta(df,n)
df1['position'] = 0
df1['flag'] = 0
df1['net_asset_value'] = 0
position = 0
#beta是前17天没有数据(n=18) ma20是前20天没有数据
for i in range(5,len(df1.index)-1):
if df1['stdbeta'].iloc[i] > 0.7 and df1['ma20'].iloc[i-1]>df1['ma20'].iloc[i-3] and position == 0:
df1['flag'].iloc[i] = 1
df1['position'].iloc[i+1] = 1
position = 1
elif df1['stdbeta'].iloc[i] < -0.7 and df1['ma20'].iloc[i-1]<df1['ma20'].iloc[i-3] and position == 1:
df1['flag'].iloc[i] = -1
df1['position'].iloc[i+1] = 0
position = 0
else:
df1['position'].iloc[i+1] = df1['position'].iloc[i]
df1['net_asset_value'] = (1+df1.close.pct_change(1).fillna(0)*df1.position).cumprod()
return df1
策略指标
| 统计量 | 均值优化标准分策略 |
|---|---|
| 净值 | 16.91 |
| 收益率 | 1591.22% |
| 年化收益率 | 27.36% |
| 夏普比率 | 1.48 |
| 最大回撤 | -23.61% |
| 持仓天数 | 1638 |
| 交易次数 | 37.5 |
| 平均持仓天数 | 43 |
| 盈利天数 | 714 |
| 亏损天数 | 470 |
| 胜率(按天) | 60.30% |
| 平均盈利率(按天) | 1.24% |
| 平均亏损率(按天) | -1.24% |
| 平均盈亏比(按天) | 1 |
| 盈利次数 | 26 |
| 亏损次数 | 11 |
| 单次最大盈利 | 91% |
| 单次最大亏损 | -17% |
| 胜率(按次) | 70.27% |
| 平均盈利率(按次) | 15% |
| 平均亏损率(按次) | -3% |
| 平均盈亏比(按次) | 4.6 |
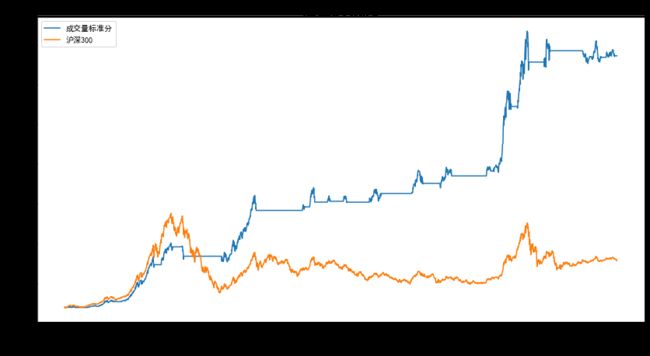
3.3.2 结合交易量相关性的优化
除却直接从近期历史价格来确认当下市场趋势状态,很多发表的研究表明市场涨跌与交易量有明显的正相关性。借鉴类似的想法,我们尝试用交易量与修正标准分之间的相关性来过滤误判信号。只有在相关性为正的时刻给出的交易信号,我们才认为是合理的信号。
优化后的策略为
- 计算 RSRS 标准分指标买卖信号。
- 如果指标发出买入信号,同时满足前 10 日交易量与修正标准分之间的相关性为正,则买入。
- 如果指标发出卖出信号,则卖出手中持股。
策略代码
#基于 RSRS 指标与交易量相关性的优化
def cal_vol_beta(df,n):
df1 = cal_stdbeta(df,n)
df1['position'] = 0
df1['flag'] = 0
df1['net_asset_value'] = 0
position = 0
for i in range(10,len(df1.index)-1):
pre_volume = df1['volume'].iloc[i-10:i]
series_beta = df1['stdbeta'].iloc[i-10:i]
#计算相关系数需要数据为series格式
corr = series_beta.corr(pre_volume,method = 'pearson')
if df1['stdbeta'].iloc[i] > 0.7 and corr > 0 and position == 0:
df1['flag'].iloc[i] = 1
df1['position'].iloc[i+1] = 1
position = 1
elif df1['stdbeta'].iloc[i] < -0.7 and position == 1:
df1['flag'].iloc[i] = -1
df1['position'].iloc[i+1] = 0
position = 0
else:
df1['position'].iloc[i+1] = df1['position'].iloc[i]
df1['net_asset_value'] = (1+df1.close.pct_change(1).fillna(0)*df1.position).cumprod()
return df1
策略指标
| 统计量 | 成交量优化标准分策略 |
|---|---|
| 净值 | 13.97 |
| 收益率 | 1296.64% |
| 年化收益率 | 25.10% |
| 夏普比率 | 1.57 |
| 最大回撤 | -22.29% |
| 持仓天数 | 916 |
| 交易次数 | 40 |
| 平均持仓天数 | 22 |
| 盈利天数 | 548 |
| 亏损天数 | 368 |
| 胜率(按天) | 59.83% |
| 平均盈利率(按天) | 1.29 |
| 平均亏损率(按天) | -1.16 |
| 平均盈亏比(按天) | 1.11 |
| 盈利次数 | 27 |
| 亏损次数 | 13 |
| 单次最大盈利 | 79% |
| 单次最大亏损 | -16% |
| 胜率(按次) | 67.50% |
| 平均盈利率(按次) | 13% |
| 平均亏损率(按次) | -4% |
| 平均盈亏比(按次) | 3.71 |
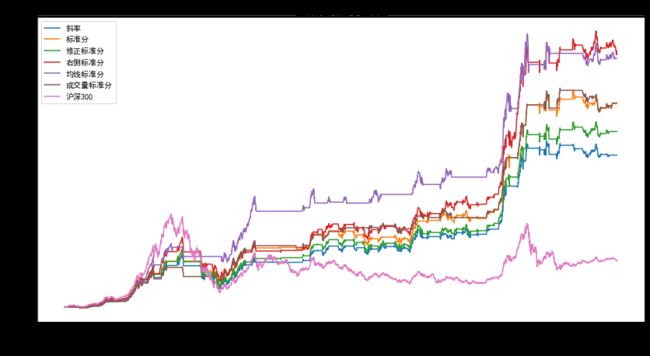
3.4 策略结果汇总
现在给出所有RSRS策略的净值曲线和统计数据
| 统计量 | 斜率 | 标准分 | 修正标准分 | 右偏标准分 | 均值优化标准分 | 成交量优化标准分 |
|---|---|---|---|---|---|---|
| 净值 | 10.66 | 13.93 | 12.15 | 17.67 | 16.91 | 13.97 |
| 收益率 | 965.73% | 1292.70% | 1115.40% | 1667.22% | 1591.22% | 1296.64% |
| 年化收益率 | 21.92% | 25.07% | 23.47% | 27.88% | 27.36% | 25.10% |
| 夏普比率 | 1.16 | 1.28 | 1.19 | 1.29 | 1.48 | 1.57 |
| 最大回撤 | -50.26% | -50.26% | -51.28% | -51.16% | -23.61% | -22.29% |
| 持仓天数 | 1184 | 1298 | 1397 | 1638 | 1638 | 916 |
| 交易次数 | 21 | 67 | 46 | 37.5 | 37.5 | 40 |
| 平均持仓天数 | 56 | 19 | 30 | 43 | 43 | 22 |
| 盈利天数 | 747 | 741 | 790 | 928 | 714 | 548 |
| 亏损天数 | 575 | 557 | 607 | 710 | 470 | 368 |
| 胜率(按天) | 56.51% | 57.09% | 56.55% | 56.65% | 60.30% | 59.83% |
| 平均盈利率(按天) | 1.31% | 1.32% | 1.30% | 1.27% | 1.24% | 1.29 |
| 平均亏损率(按天) | -1.25% | -1.25% | -1.25% | -1.22% | -1.24% | -1.16 |
| 平均盈亏比(按天) | 1.05 | 1.06 | 1.05 | 1.04 | 1 | 1.11 |
| 盈利次数 | 16 | 40 | 32 | 26 | 26 | 27 |
| 亏损次数 | 5 | 26 | 14 | 11 | 11 | 13 |
| 单次最大盈利 | 170% | 91% | 76% | 91% | 91% | 79% |
| 单次最大亏损 | -12% | -41% | -18% | -17% | -17% | -16% |
| 胜率(按次) | 76.19% | 60.61% | 69.57% | 70.27% | 70.27% | 67.50% |
| 平均盈利率(按次) | 25% | 18% | 11% | 15% | 15% | 13% |
| 平均亏损率(按次) | -3% | -9% | -3% | -3% | -3% | -4% |
| 平均盈亏比(按次) | 7.86 | 2.05 | 3.3 | 4.6 | 4.6 | 3.71 |
4.总结
本文基本复现了【光大证券-基于阻力支撑相对强度(RSRS)的市场择时】的研究内容,同时得到了与原研报相近的结果。
本文的不足:
1.没有考虑交易成本。原研报同时给出了在不同交易成本下各策略的结果,净值有略微的下降。
2.没有给出选取不同N、M时策略的表现情况。
5.本文作者
何百圣 哈尔滨工业大学威海校区 经济管理学院
蔡金航 哈尔滨工业大学威海校区 计算机科学与技术学院
写在最后
我们是国内普通高校的在校学生,同时也是量化投资的初学者。我们的学校不是清北复交,也没有金融工程实验室,同时地处三线小城,因此我们在校期间较难获得量化实习机会,但我们期待与业界进行沟通、交流。
蔡金航同学是我们其中的一员。其在寻找暑期量化实习时,收到了几家私募和券商金工组的笔试邀请,笔试内容皆为在给定时间内复现出一篇金工研报。蔡同学受到启发,发觉复现金工研报是我们学习量化策略、锻炼程序设计能力同时也是与业界交流的很好的途径。
在蔡同学的建议下,我们开启研报复现系列的创作,记录我们的学习过程,并将我们的创作内容分享出来,与读者们一起交流、学习、进步。
我们的水平有限,创作的内容难免会有错误或不严谨的内容,我们欢迎读者的批评指正。
如果您对我们的内容感兴趣,请联系我们:[email protected]