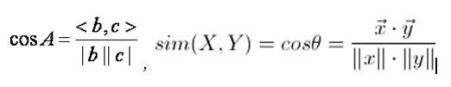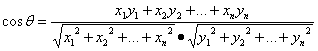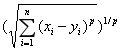提到检索的方法,比如KNN算法,这些都需要用到“距离”这个尺度去度量两者的近似程度。但是,距离也有很多种,除了我们熟悉的欧氏距离之外,其实还有很多。。。
余弦距离:
是一种衡量两个向量相关程度的尺度。利用两个向量的余弦值,由于在0到90度之间,的值为减函数,所以当cos(theta)值越大,theta值越小。体现的是两个向量方向上的差异。对数值绝对值不敏感。
对于向量x=(x1,x2,x3,...,xn)和向量y=(y1,y2,y3,...yn)之间的夹角:
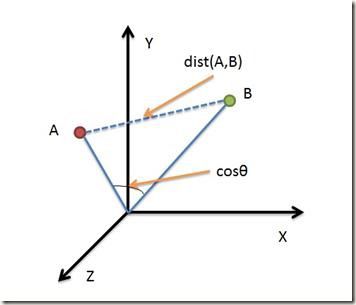
其更注重两个向量方向的夹角之间的距离,而不是欧氏距离里的直接距离。
欧氏距离与余弦距离:
欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异;而余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦相似度对绝对数值不敏感)。
明可夫斯基距离(Minkowski Distance)
明氏距离是欧氏距离的推广,是对多个距离度量公式的概括性的表述。公式如下:
p可以取任意正整数。
皮尔森相关系数(Pearson Correlation Coefficient):
即相关分析中的相关系数r,分别对X和Y基于自身总体标准化后计算空间向量的余弦夹角。公式如下:
Jaccard相似系数(Jaccard Coefficient):
Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。如果比较X与Y的Jaccard相似系数,只比较xn和yn中相同的个数,公式如下:
针对余弦相似度对数值大小的不敏感,出现了修正余弦相似度(Adjusted cosine similaarity):每个数值都减去一个自己的均值,这样归一化后,可以使得向量夹角的距离变得符合现实。
虽然余弦相似度对个体间存在的偏见可以进行一定的修正,但是因为只能分辨个体在维之间的差异,没法衡量每个维数值的差异,会导致这样一个情况:比如用户对内容评分,5分制,X和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得出的结果是0.98,两者极为相似,但从评分上看X似乎不喜欢这2个内容,而Y比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性,就出现了调整余弦相似度,即所有维度上的数值都减去一个均值,比如X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
哈明距离(汉明距离)
汉明距离是使用在数据传输差错控制编码里面的,汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量,我们以d(x,y)表示两个字x,y之间的汉明距离。对两个字符串进行异或运算,并统计结果为1的个数,那么这个数就是汉明距离。
比如:
1011101 与 1001001 之间的汉明距离是 2。
2143896 与 2233796 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
这种方法往往可以进行一定的模板匹配,计算与模板的接近程度。