KMP原理

一、需要知道的概念

前缀：字符串A和B，A=B+S，S非空，则B为A的前缀。
后缀：A=S+B，S非空，则B为A的后缀。
PMT：前缀集合和后缀集合的交集中，最长元素的长度
部分匹配表：PMT值集合，字符串所有前缀的PMT值
prefix：每一个下标位置对应一个PMT值，组成的数组
next：prefix向右移一个下标位置，组成next数组

下面的图看不懂不要紧，看完原理就懂了！

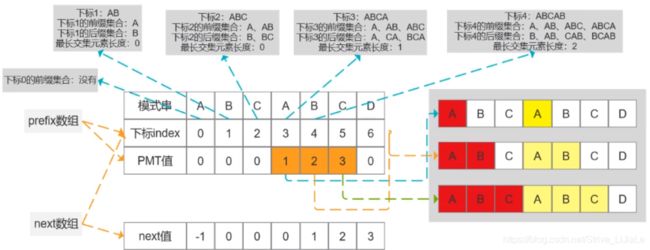
例如：
下标5：ABCABC
前缀集合：A，AB，ABC，ABCA，ABCAB
后缀集合：C，BC，ABC，CABC，BCABC
最长交集长度：3（ABC）

二、KMP原理

1.为什么要求交集？

（上面是主串，下面是模式串）
1.开始第一次比较，比较到模式串的最后一位D，与主串A失配，如图所示：

就要右移模式串继续比较：

2.其实就是将模式串的前缀BCADBC与主串后缀CADBCA相比较，第一位失配，右移
3.接着前缀BCADB与后缀ADBCA比较，第一位失配，右移
4.接着前缀BCAD与后缀DBCA比较，第一位失配，右移
5.接着前缀BCA与后缀BCA比较，匹配成功

可以发现，每次移动都是前缀集合与后缀集合的比较。寻找主串后缀集合与模式串前缀集合相同的部分（不相同，最后肯定不匹配），即交集。
如果找到交集，就可以直接移过去，省了4步，跳过很多没必要的操作。

为了将这些交集方便使用，就存储到PMT数组内。

2.PMT数组作用

模式串与主串进行比对时，需要索引，设i为主串索引，j为模式串索引。
当比较到最后一位时，i = 6，j = 6.
有了交集BC，长度为2，这个信息会存入PMT数组内。
要提高效率，就要实现对齐，需要移动的元素的位置信息（即下标）就是交集长度（被保存在PMT数组中），就是将A移动到D（用 j 记录）的位置，让 j 重新指向A的下标2即可，称为回溯


动态图演示：
txt主串；pat模式串。

这就是KMP 算法原理，即永不回退 主串的指针 i，不走回头路（不会重复扫描 主串），而是借助 PMT 数组中储存的信息把 模式串 移到正确的位置继续匹配
后面需要求得next数组，其实和PMT作用一样，只是为了写代码实现方便。

KMP 算法的难点在于，如何计算 next 数组中的信息？如何根据这些信息正确地移动 模式串 的指针？

3.为什么求模式串的交集

其实，模式串与主串第一次比较的时候，除了失配那一位，失配前那部分都是相同的。
接下来的比较操作，可以理解为那部分的自己前缀和自己后缀比较。

即模式串：BCADBCD，最后一位失配
失配前那部分：BCADBC。
步骤和之前一样，直到找到交集BC。
如上面所列举的下标5的例子，找出自己的前缀和后缀的交集。

4.用KMP求next数组

前提条件：

对于模式串：A B C A B C D
index索引：[ 0, 1, 2, 3, 4, 5, 6 ]
将模式串复制一份（灰色），后移一位，拿灰色前缀与模式串后缀匹配。
先当于再进行一遍KMP算法，同样遇到KMP难点，如何计算 next 数组中的信息？如何根据这些信息正确地移动 灰色的指针？
利用KMP 算法原理，即永不回退 模式串 的指针 i，不走回头路（不会重复扫描 模式串），而是借助 next 数组中储存的信息把 灰色串 移到正确的位置继续匹配

i 是模式串的索引，j是灰色的索引
为了当不匹配时，让灰色后移后，继续与模式串下一位开始比较，需要i++，j++，并且使得 j 要从0开始（从灰色第一个元素开始），就需要以 j= -1为灰色整体右移信息，即失配时就要置为-1，正好j+1=0。

匹配时，j++即可。
如此一来，j就提供了信息：j的值 就是灰色与模式串在 i 之前匹配的个数，也就是交集的长度，也就是PMT[ i ]所需要的值，也就是next[i+1]的值。

思考一下，next[ j ]存储的内容和 j 的关系？
next[ j ] = PMT[ j - 1 ]
就是 j所指位置 的前一位置的匹配个数，即交集长度。
如果 j所指的位置失配， 就需要移动灰色串，要移动多少呢？（j要指向下标是多少呢？）
信息就在next [ j ]里。即令j = next [ j ] 来实现回溯。
next数组代替PMT数组带来的编码好处就体现出来了

第一步：i=0，
i 指向的 A（红色标记），只有一个元素没有前后缀，所以没有交集.j=-1
PMT [ 0 ]=0，next [ 0 ]= -1，
使 i 和 j 右移，进行下一次比对

第二步：i = 1，j=0
next[i]的值，是上一步PMT[i]的值（记录上一步交集长度，匹配的元素个数，j的值）,next[ 1 ] = PMT[ 0 ] = 0；
j 指向索引0的位置A，失配
j = next [ 0 ] = -1;
使 i 和 j 右移，进行下一次比对

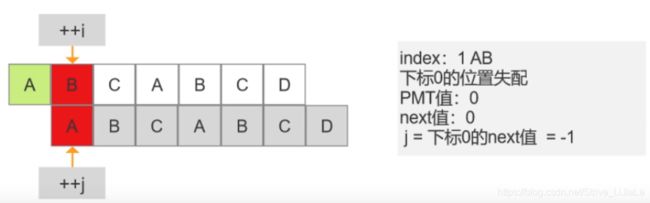
第三步：i = 2，
j指向索引0的位置A，失配
j = next [0] = -1，使 i 和 j 右移，进行下一次比对

第四步：i = 3，
j=0 ，j指向索引0的位置A，匹配
j=j+1=1,使 i 和 j 右移，进行下一次比对
有交集，给数组赋值
PMT [ 3 ] = 1 。
next[ 3 ] = 0

第五步：i = 4，j =1， 匹配。给数组赋值
使 i 和 j 右移，进行下一次比对

第六步：i = 5，j = 2，匹配。给数组赋值
使 i 和 j 右移，进行下一次比对

第七步：i = 6，j = 3
i指向D，j指向索引3的位置A，失配

代码

//字符串匹配
    static int search(char[] str,char[] pattern,int[] next){
     
        int i = 0;
        int j = 0;

        while (i< str.length&&j< pattern.length){
     
            if (j==-1||str[i] == pattern[j]){
     
                i++;
                j++;
            }
            else{
     
                j = next[j];			//回溯，右移
            }
        }
        if (j== pattern.length)
            return i - 1;
        else {
     
            return -1;
        }
    }
//求模式串的next数组
    static void getNext(char[] pattern,int[] next){
     
        next[0] = -1;
        int i = 0,j = -1;

        while (i< pattern.length){
     
            if(j == -1){
                     //，j=-1，空
                i++;
                j++;
            }else if (pattern[i] == pattern[j]){
     
                i++;j++;
                next[i] = j;
            }else {
     
                j = next[j];			//回溯，右移
            }
        }
    }