计算机视觉中的各种卷积(Convolution in Computer Vision)

1. 卷积与互相关Cross-correlation

在信号处理、图像处理和其它工程/科学领域，卷积都是一种使用广泛的技术。但是，深度学习领域的卷积本质上是信号/图像处理领域内的互相关（cross-correlation）。这两种操作之间存在细微的差别。
在信号/图像处理领域，卷积的定义是：

其定义是一个函数经过反转和位移后 g(t - t’) 和另一个函数 f(t’) 相乘得到的积f(t’) * g(t - t’) 的积分。在信号处理中，函数 g 是过滤器。它被反转后再沿水平轴滑动。在每一个位置，我们都计算 f 和反转后的 g 之间相交区域的面积。这个相交区域的面积就是特定位置处的卷积值。计算过程可视化如下：

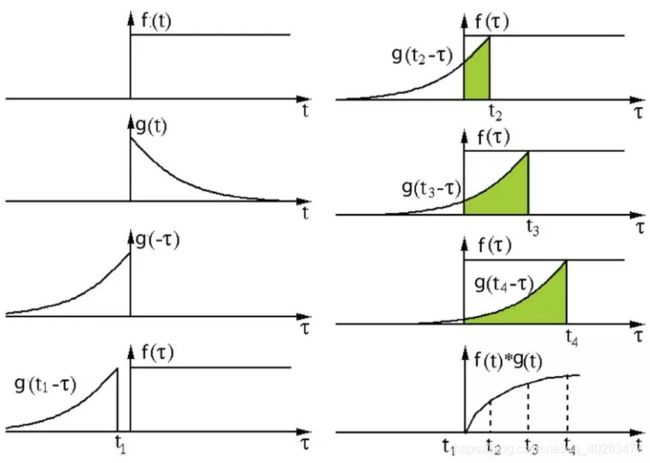
在信号处理中，与标准的卷积运算不同的是互相关是两个函数之间的滑动点积或滑动内积。互相关中的过滤器不经过反转，而是直接滑过函数 f。f 与 g 之间的交叉区域即是互相关。下图展示了卷积与互相关之间的差异。

Note：在深度学习中，卷积中的过滤器不经过反转。严格来说，这是互相关，本质上是执行逐元素乘法和加法。但在深度学习中，直接将其称之为卷积更加方便。这没什么问题，因为过滤器的权重是在训练阶段学习到的。如果上面例子中的反转函数 g 是正确的函数，那么经过训练后，学习得到的过滤器看起来就会像是反转后的函数 g。因此，在训练之前，没必要像在真正的卷积中那样首先反转过滤器。

2. 深度学习中的卷积（单通道版本，多通道版本）(single channel version, multi-channel version)

单通道和多通道也就是 filter 的个数不同，个数为1则输出 single channel ，个数为多个则输出 multi-channel。

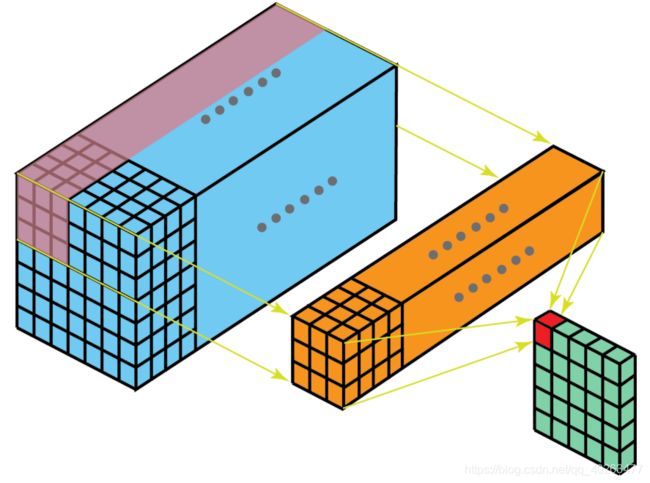
3. 3D 卷积

• 当过滤器深度与输入层深度一样时，在对一个 3D 体积执行卷积，仍在深度学习中称之为 2D 卷积。因为这个 3D 过滤器仅沿两个方向移动（图像的高和宽），这种操作的输出是一张 2D 图像（仅有一个通道）。
  
• 而当过滤器深度小于输入层深度（核大小<通道大小）时，3D 过滤器可以在所有三个方向（图像的高度、宽度、通道）上移动。在每个位置，逐元素的乘法和加法都会提供一个数值。因为过滤器是滑过一个 3D 空间，所以输出数值也按 3D 空间排布，也就是说输出是一个 3D 数据。
  
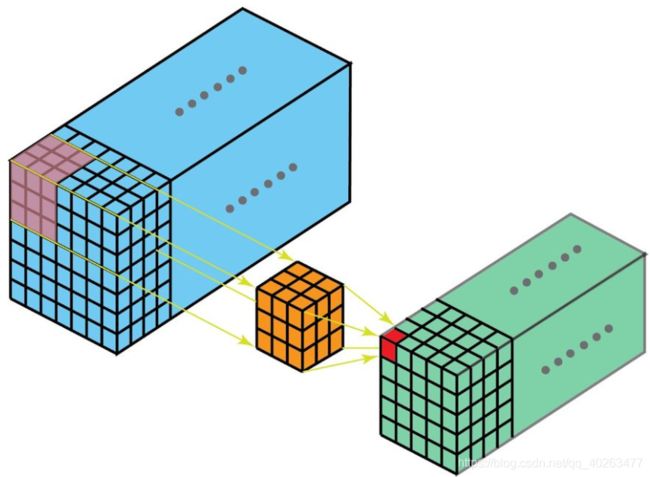
• 与 2D 卷积（编码了 2D 域中目标的空间关系）类似，3D 卷积可以描述 3D 空间中目标的空间关系。对某些应用（比如生物医学影像中的 3D 分割/重构）而言，这样的 3D 关系很重要，比如在 CT 和 MRI 中，血管之类的目标会在 3D 空间中蜿蜒曲折。

4. 1×1 卷积

Since we talked about depth-wise operation in the previous section of 3D convolution, let’s look at another interesting operation, 1 x 1 convolution.

You may wonder why this is helpful. Do we just multiply a number to every number in the input layer? Yes and No. The operation is trivial for layers with only one channel. There, we multiply every element by a number.

Things become interesting if the input layer has multiple channels. The following picture illustrates how 1 x 1 convolution works for an input layer with dimension H x W x D. After 1 x 1 convolution with filter size 1 x 1 x D, the output channel is with dimension H x W x 1. If we apply N such 1 x 1 convolutions and then concatenate results together, we could have a output layer with dimension H x W x N.

Initially, 1 x 1 convolutions were proposed in the Network-in-network paper. They were then highly used in the Google Inception paper. A few advantages of 1 x 1 convolutions are:

• Dimensionality reduction for efficient computations
• Efficient low dimensional embedding, or feature pooling
• Applying nonlinearity again after convolution

The first two advantages can be observed in the image above. After 1 x 1 convolution, we significantly reduce the dimension depth-wise. Say if the original input has 200 channels, the 1 x 1 convolution will embed these channels (features) into a single channel. The third advantage comes in as after the 1 x 1 convolution, non-linear activation such as ReLU can be added. The non-linearity allows the network to learn more complex function.

5. 卷积算术Convolution Arithmetic

6. 转置卷积（去卷积、棋盘效应）Transposed Convolution (Deconvolution, checkerboard artifacts)

• 对于很多网络架构的很多应用而言，往往需要进行与普通卷积（下采样）方向相反的转换，即希望执行上采样。例子包括生成高分辨率图像以及将低维特征图映射到高维空间，比如在自动编码器或语义分割中。（在后者的例子中，语义分割首先会提取编码器中的特征图，然后在解码器中恢复原来的图像大小，使其可以分类原始图像中的每个像素。）
• 在传统的方法中实现上采样是应用插值方案或人工创建规则。而神经网络等现代架构则倾向于让网络自动学习合适的变换，无需人类干预。
• 转置卷积在文献中也被称为去卷积或 fractionally strided convolution。但是，需要指出“去卷积（deconvolution）”这个名称并不是很合适，因为转置卷积并非信号/图像处理领域定义的那种真正的去卷积（deconvolution）。从技术上讲，信号处理中的去卷积是卷积运算的逆运算，但深度学习中却不是这种运算。因此，某些作者强烈反对将转置卷积称为去卷积（deconvolution）。人们称之为去卷积（deconvolution）主要是因为这样说更简单。

计算过程可视化例子：

• 在一个 2×2 的输入（周围加了 2×2 的单位步长的零填充）上应用一个 3×3 核的转置卷积。上采样输出的大小是 4×4。
  
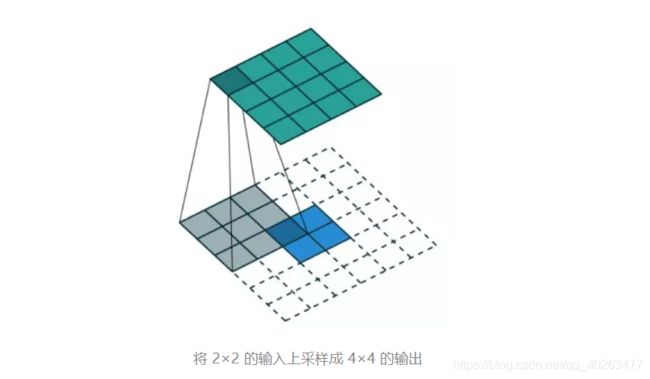
• 通过应用各种填充和步长，可以将同样的 2×2 输入图像映射到不同的图像尺寸。下面，转置卷积被用在了同一张 2×2 输入上（输入之间插入了一个零，并且周围加了 2×2 的单位步长的零填充），所得输出的大小是 5×5。
  

普通卷积 / 转置卷积的矩阵实现
定义：C 为卷积核，Large 为输入图像，Small 为输出图像。经过卷积（矩阵乘法）后，可以将大图像下采样为小图像。这种矩阵乘法的卷积的实现遵照：C x Large = Small。
具体实现：如下图例子所示，将输入平展为 16×1 的矩阵，并将卷积核转换为一个稀疏矩阵（4×16）。然后，在稀疏矩阵和平展的输入之间使用矩阵乘法。之后，再将所得到的矩阵（4×1）转换为 2×2 的输出。

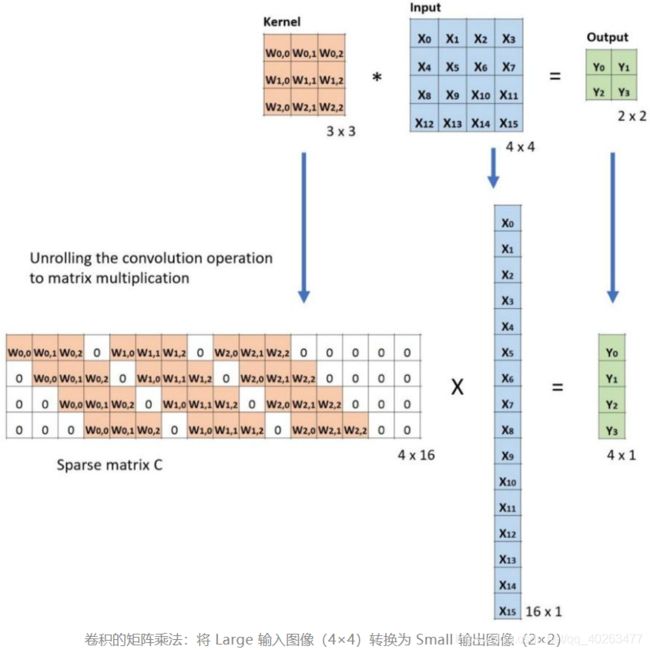
在上图中等式的两边都乘上矩阵的转置 C^T，并借助“一个矩阵与其转置矩阵的乘法得到一个单位矩阵”这一性质，那么我们就能得到公式 C^T x Small = Large，如下图所示。实现了从小图像到大图像的上采样的目标，转置卷积中的“转置”因此而来。
转置矩阵的算术解释可参阅：https://arxiv.org/abs/1603.07285

Checkerboard artifacts
One unpleasant behavior that people observe when using transposed convolution is the so-called checkerboard artifacts.

The paper “Deconvolution and Checkerboard Artifacts” has an excellent description about this behavior. Please check out this article for more details. Here, I just summarize a few key points.

Checkerboard artifacts result from “uneven overlap” of transposed convolution. Such overlap puts more of the metaphorical paint in some places than others.

In the image below, the layer on the top is the input layer, and the layer on the bottom is the output layer after transposed convolution. During transposed convolution, a layer with small size is mapped to a layer with larger size.

In the example (a), the stride is 1 and the filer size is 2. As outlined in red, the first pixel on the input maps to the first and second pixels on the output. As outlined in green, the second pixel on the input maps to the second and the third pixels on the output. The second pixel on the output receives information from both the first and the second pixels on the input. Overall, the pixels in the middle portion of the output receive same amount of information from the input. Here exist a region where kernels overlapped. As the filter size is increased to 3 in the example (b), the center portion that receives most information shrinks. But this may not be a big deal, since the overlap is still even. The pixels in the center portion of the output receive same amount of information from the input.

Now for the example below, we change stride = 2. In the example (a) where filter size = 2, all pixels on the output receive same amount of information from the input. They all receive information from a single pixel on the input. There is no overlap of transposed convolution here.

If we change the filter size to 4 in the example (b), the evenly overlapped region shrinks. But still, one can use the center portion of the output as the valid output, where each pixel receives the same amount of information from the input.

However, things become interesting if we change the filter size to 3 and 5 in the example © and (d). For these two cases, every pixel on the output receives different amount of information compared to its adjacent pixels. One cannot find a continuous and evenly overlapped region on the output.

The transposed convolution has uneven overlap when the filter size is not divisible by the stride. This “uneven overlap” puts more of the paint in some places than others, thus creates the checkerboard effects. In fact, the unevenly overlapped region tends to be more extreme in two dimensions. There, two patterns are multiplied together, the unevenness gets squared.

Two things one could do to reduce such artifacts, while applying transposed convolution. First, make sure you use a filer size that is divided by your stride, avoiding the overlap issue. Secondly, one can use transposed convolution with stride = 1, which helps to reduce the checkerboard effects. However, artifacts can still leak through, as seen in many recent models.

The paper further proposed a better up-sampling approach: resize the image first (using nearest-neighbor interpolation or bilinear interpolation) and then do a convolutional layer. By doing that, the authors avoid the checkerboard effects. You may want to try it for your applications.

7. 扩张卷积Dilated Convolution (Atrous Convolution)

别名：空洞卷积，膨胀卷积，多孔卷积，带孔卷积
扩张卷积由这两篇论文引入：

• Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs（2014）
• Multi-Scale Context Aggregation by Dilated Convolutions（2015）

这是一个标准的卷积：

扩张卷积如下：

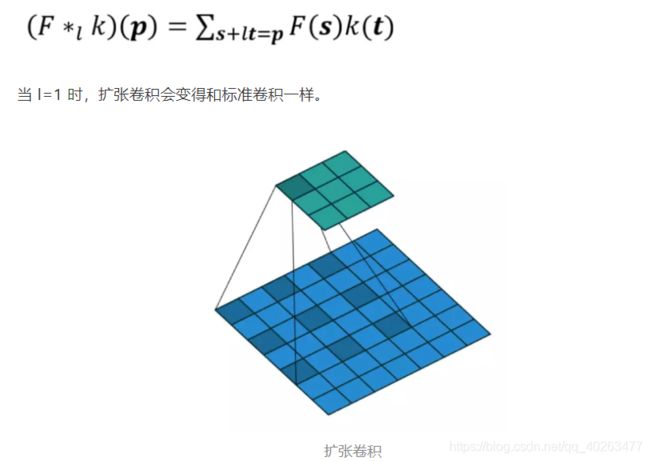
直观而言，扩张卷积就是通过在核元素之间插入空格来使核“膨胀”。新增的参数 l（扩张率）表示希望将核加宽的程度。具体实现可能各不相同，但通常是在核元素之间插入 l-1 个空格。下图展示了 l = 1, 2, 4 时的核大小。

由图可见，l=1 时感受野为 3×3，l=2 时为 7×7。l=3 时，感受野的大小就增加到了 15×15。值得注意的是，与这些操作相关的参数数量是相等的，均为3x3。从而说明「观察」更大的感受野不会有额外的成本。因此，扩张卷积可用于廉价地增大输出单元的感受野，而不会增大其核大小，这在多个扩张卷积彼此堆叠时尤其有效。

8. 可分卷积（空间可分卷积，深度可分卷积） (Spatially Separable Convolution, Depthwise Separable Convolution)

1、空间可分卷积
空间可分卷积操作的是图像的 2D 空间维度，即高和宽。从概念上看，空间可分卷积是将一个卷积分解为两个单独的运算。对于下面的示例，3×3 的 Sobel 核被分成了一个 3×1 核和一个 1×3 核。

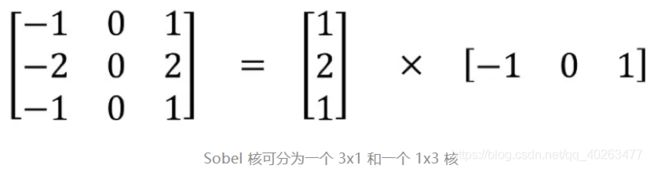
在卷积中，3×3 核直接与图像卷积。在空间可分卷积中，3×1 核首先与图像卷积，然后再应用 1×3 核卷积。这样，执行同样的操作时仅需 6 个参数，而不是 9 个。此外，使用空间可分卷积时所需的矩阵乘法也更少。例如，5×5 图像与 3×3 核的卷积（步幅=1，填充=0）要求在 3 个位置水平地扫描核（还有 3 个垂直的位置），总共就是 9 个位置，表示为下图中的点。在每个位置，会应用 9 次逐元素乘法。总共就是 9×9=81 次乘法。

另一方面，对于空间可分卷积，首先在 5×5 的图像上应用一个 3×1 的过滤器，可以在水平 5 个位置和垂直 3 个位置扫描这样的核。总共就是 5×3=15 个位置，表示为下图中的点。在每个位置，会应用 3 次逐元素乘法。总共就是 15×3=45 次乘法。现在得到了一个 3×5 的矩阵。这个矩阵再与一个 1×3 核卷积，即在水平 3 个位置和垂直 3 个位置扫描这个矩阵。对于这 9 个位置中的每一个，应用 3 次逐元素乘法。这一步需要 9×3=27 次乘法。因此，总体而言，空间可分卷积需要 45+27=72 次乘法，少于普通卷积。

一般化推广
假设现在将卷积应用于一张 N×N 的图像上，卷积核为 m×m，步幅为 1，填充为 0。传统卷积需要 (N-2) x (N-2) x m x m 次乘法，空间可分卷积需要 N x (N-2) x m + (N-2) x (N-2) x m = (2N-2) x (N-2) x m 次乘法。空间可分卷积与标准卷积的计算成本比为：

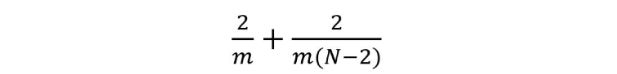
因为图像尺寸 N 远大于过滤器大小（N>>m），所以这个比就变成了 2/m。也就是说，在这种渐进情况（N>>m）下，当过滤器大小为 3×3 时，空间可分卷积的计算成本是标准卷积的 2/3。过滤器大小为 5×5 时这一数值是 2/5；过滤器大小为 7×7 时则为 2/7。
存在的问题：
尽管空间可分卷积能节省成本，但深度学习却很少使用它。一大主要原因是并非所有的核都能分成两个更小的核。如果用空间可分卷积替代所有的传统卷积，那么就限制了在训练过程中搜索所有可能的核。这样得到的训练结果可能是次优的。
2、深度可分卷积
首先快速回顾标准的 2D 卷积。举一个具体例子，假设输入层的大小是 7×7×3（高×宽×通道），而过滤器的大小是 3×3×3。经过与一个过滤器的 2D 卷积之后，输出层的大小是 5×5×1（仅有一个通道）。

一般来说，两个神经网络层之间会应用多个过滤器。假设这里有 128 个过滤器。在应用了这 128 个 2D 卷积之后，将有 128 个 5×5×1 的输出映射图（map）。然后将这些映射图堆叠成大小为 5×5×128 的单层。通过这种操作，可将输入层（7×7×3）转换成输出层（5×5×128）。空间维度（即高度和宽度）会变小，而深度会增大。

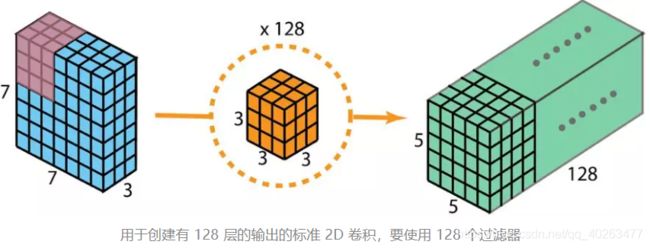
使用深度可分卷积，目的就是利用1×1 卷积核实现同样的变换。

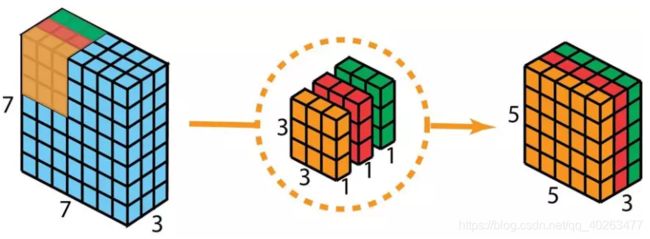
• 首先，将深度卷积应用于输入层。但不使用 2D 卷积中大小为 3×3×3 的单个过滤器，而是分开使用 3 个核。每个过滤器的大小为 3×3×1。每个核与输入层的一个通道卷积。每个这样的卷积都能提供大小为 5×5×1 的映射图。然后将这些映射图堆叠在一起，创建一个 5×5×3 的图像。经过这个操作之后，就可以得到大小为 5×5×3 的输出。

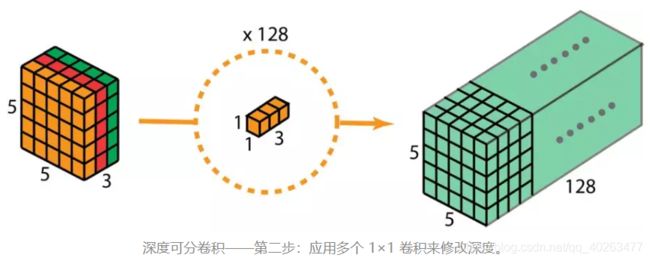
• 然后，为了扩展深度，应用128个核大小为 1×1×3 的 1×1 卷积。将 5×5×3 的输入图像与每个 1×1×3 的核卷积，可得到大小为 5×5×128 的映射图。

下图展示了深度可分卷积的整个过程：

深度可分卷积的优点：

• 在 2D 普通卷积例子中的计算成本，有 128 个 3×3×3 个核移动了 5×5 次，也就是 128 x 3 x 3 x 3 x 5 x 5 = 86400 次乘法。而在深度可分卷积中，第一个深度卷积步骤，有 3 个 3×3×1 核移动 5×5 次，也就是 3x3x3x1x5x5 = 675 次乘法。在 1×1 卷积的第二步，有 128 个 1×1×3 核移动 5×5 次，即 128 x 1 x 1 x 3 x 5 x 5 = 9600 次乘法。因此，深度可分卷积共有 675 + 9600 = 10275 次乘法。这样的成本大概仅有 2D 卷积的 12%！
• 一般化说明效率高。对于大小为 H×W×D 的输入图像，如果使用 Nc 个大小为 h×h×D 的核执行 2D 卷积（步幅为 1，填充为 0，其中 h 是偶数）。为了将输入层（H×W×D）变换到输出层（(H-h+1)x (W-h+1) x Nc），所需的总乘法次数为：Nc x h x h x D x (H-h+1) x (W-h+1)。另一方面，对于同样的变换，深度可分卷积所需的乘法次数为：D x h x h x 1 x (H-h+1) x (W-h+1) + Nc x 1 x 1 x D x (H-h+1) x (W-h+1) = (h x h + Nc) x D x (H-h+1) x (W-h+1)。则深度可分卷积与 2D 卷积所需的乘法次数比为：
  
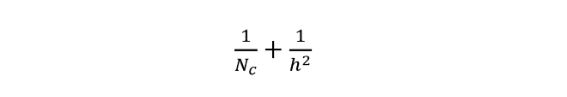
  现代大多数架构的输出层通常都有很多通道，可达数百甚至上千。对于这样的层（Nc >> h），则上式可约简为 1 / h²。基于此，如果使用 3×3 过滤器，则 2D 卷积所需的乘法次数是深度可分卷积的 9 倍。如果使用 5×5 过滤器，则 2D 卷积所需的乘法次数是深度可分卷积的 25 倍。

深度可分卷积的坏处：
因为利用1x1的卷积核来代替3x3卷积核以达到相同的 channel 深度，从而降低了卷积中参数的数量。因此，对于较小的模型而言，如果用深度可分卷积替代 2D 卷积，模型的表达能力可能会显著下降，致使得到的模型可能是次优的。但是，如果使用得当，深度可分卷积能在不降低模型性能的前提下实现效率的提升。

9. 平展卷积Flattened Convolution

The flattened convolution was introduced in the paper “Flattened convolutional neural networks for feedforward acceleration”. Intuitively, the idea is to apply filter separation. Instead of applying one standard convolution filter to map the input layer to an output layer, we separate this standard filter into 3 1D filters. Such idea is similar as that in the spatial separable convolution described above, where a spatial filter is approximated by two rank-1 filters.

One should notice that if the standard convolution filter is a rank-1 filter, such filter can always be separated into cross-products of three 1D filters. But this is a strong condition and the intrinsic rank of the standard filter is higher than one in practice. As pointed out in the paper “As the difficulty of classification problem increases, the more number of leading components is required to solve the problem… Learned filters in deep networks have distributed eigenvalues and applying the separation directly to the filters results in significant information loss.”

To alleviate such problem, the paper “Flattened Convolutional Neural Networks for Feedforward Acceleration” restricts connections in receptive fields so that the model can learn 1D separated filters upon training. The paper claims that by training with flattened networks that consists of consecutive sequence of 1D filters across all directions in 3D space provides comparable performance as standard convolutional networks, with much less computation costs due to the significant reduction of learning parameters.

10. 分组卷积Grouped Convolution

AlexNet 论文在 2012 年引入了分组卷积。实现分组卷积的主要原因是让网络训练可在 2 个内存有限（每个 GPU 有 1.5 GB 内存）的 GPU 上进行。下面图中的 AlexNet 表明在大多数层中都有两个分开的卷积路径。这是在两个 GPU 上执行模型并行化（当然如果可以使用更多 GPU，还能执行多 GPU 并行化）。

分组卷积的工作方式
首先，典型的 2D 卷积的步骤如下图所示。在这个例子中，通过应用 128 个大小为 3×3×3 的过滤器将输入层（7×7×3）变换到输出层（5×5×128）。推广而言，即通过应用 Dout 个大小为 h x w x Din 的核将输入层（Hin x Win x Din）变换到输出层（Hout x Wout x Dout）。

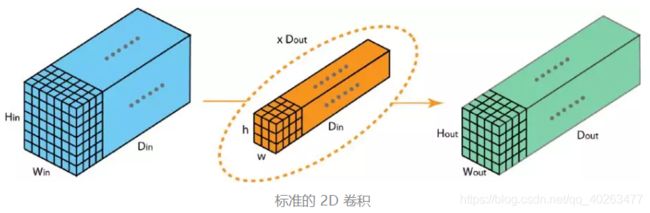
在分组卷积中，过滤器会被分为 不同的组 。每一组都负责 特定深度 的典型 2D 卷积。

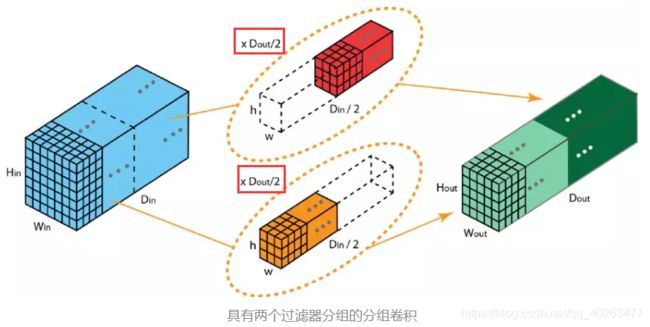
上图展示了具有两个过滤器分组的分组卷积。在每个过滤器分组中，每个过滤器的深度仅有名义上的 2D 卷积的一半。它们的深度是 Din/2。每个过滤器分组包含 Dout/2 个过滤器。第一个过滤器分组（红色）与输入层的前一半（[:, :, 0:Din/2]）卷积，而第二个过滤器分组（橙色）与输入层的后一半（[:, :, Din/2:Din]）卷积。因此，每个过滤器分组都会创建 Dout/2 个通道。整体而言，两个分组会创建 2×Dout/2 = Dout 个通道。然后我们将这些通道堆叠在一起，得到有 Dout 个通道的输出层。

分组卷积的优点：

• 第一个优点是高效训练。因为卷积被分成了多个路径，每个路径都可由不同的 GPU 分开处理，所以模型可以并行方式在多个 GPU 上进行训练。相比于在单个 GPU 上完成所有任务，这样的在多个 GPU 上的模型并行化能让网络在每个步骤处理更多图像。人们一般认为模型并行化比数据并行化更好。后者是将数据集分成多个批次，然后分开训练每一批。但是，当批量大小变得过小时，我们本质上是执行随机梯度下降，而非批梯度下降。这会造成更慢，有时候更差的收敛结果。在训练非常深的神经网络时，分组卷积会非常重要，正如在 ResNeXt 中那样。
  
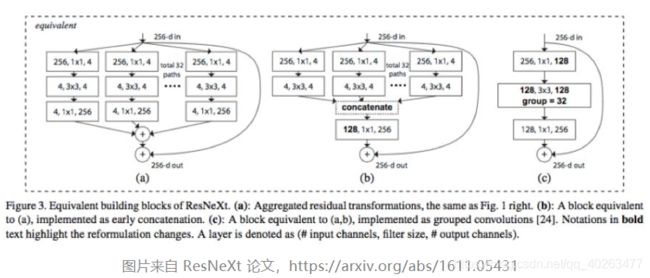
• 第二个优点是模型会更高效，即模型参数会随过滤器分组数的增大而减少。在之前的例子中，完整的标准 2D 卷积有 h x w x Din x Dout 个参数。具有 2 个过滤器分组的分组卷积有 (h x w x Din/2 x Dout/2) x 2 个参数。参数数量减少了一半。
• 第三个优点模型性能更好。分组卷积也许能提供比标准完整 2D 卷积更好的模型。另一篇出色的博客已经解释了这一点：https://blog.yani.io/filter-group-tutorial。这里简要总结一下。

模型性能更好的原因和稀疏过滤器的关系有关。下图是相邻层过滤器的相关性。其中的关系是稀疏的。

分组矩阵的相关性映射图如下：

上图是当用 1、2、4、8、16 个过滤器分组训练模型时，相邻层的过滤器之间的相关性。那篇文章提出了一个推理：过滤器分组的效果是在通道维度上学习块对角结构的稀疏性……在网络中，具有高相关性的过滤器是使用过滤器分组以一种更为结构化的方式学习到。从效果上看，不必学习的过滤器关系就不再参数化。这样显著地减少网络中的参数数量能使其不容易过拟合，因此，一种类似正则化的效果让优化器可以学习得到更准确更高效的深度网络。 此外，每个过滤器分组都会学习数据的一个独特表征。正如 AlexNet 的作者指出的那样，过滤器分组似乎会将学习到的过滤器结构性地组织成两个不同的分组——黑白过滤器和彩色过滤器。

11. 混洗分组卷积Shuffled Grouped Convolution

Shuffled grouped convolution was introduced in the ShuffleNet from Magvii Inc (Face++). ShuffleNet is a computation-efficient convolution architecture, which is designed specially for mobile devices with very limited computing power (e.g. 10–150 MFLOPs).

The ideas behind the shuffled grouped convolution are linked to the ideas behind grouped convolution (used in MobileNet and ResNeXt for examples) and depthwise separable convolution (used in Xception).

Overall, the shuffled grouped convolution involves grouped convolution and channel shuffling.

In the section about grouped convolution, we know that the filters are separated into different groups. Each group is responsible for a conventional 2D convolutions with certain depth. The total operations are significantly reduced. For examples in the figure below, we have 3 filter groups. The first filter group convolves with the red portion in the input layer. Similarly, the second and the third filter group convolves with the green and blue portions in the input. The kernel depth in each filter group is only 1/3 of the total channel count in the input layer. In this example, after the first grouped convolution GConv1, the input layer is mapped to the intermediate feature map. This feature map is then mapped to the output layer through the second grouped convolution GConv2.

Grouped convolution is computationally efficient. But the problem is that each filter group only handles information passed down from the fixed portion in the previous layers. For examples in the image above, the first filter group (red) only process information that is passed down from the first 1/3 of the input channels. The blue filter group (blue) only process information that is passed down from the last 1/3 of the input channels. As such, each filter group is only limited to learn a few specific features. This property blocks information flow between channel groups and weakens representations during training. To overcome this problem, we apply the channel shuffle.

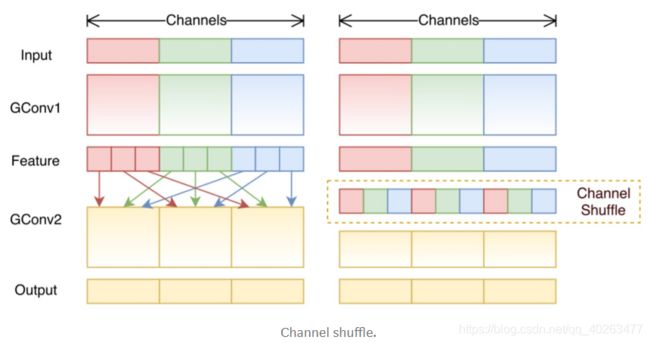
The idea of channel shuffle is that we want to mix up the information from different filter groups. In the image below, we get the feature map after applying the first grouped convolution GConv1 with 3 filter groups. Before feeding this feature map into the second grouped convolution, we first divide the channels in each group into several subgroups. The we mix up these subgroups.

After such shuffling, we continue performing the second grouped convolution GConv2 as usual. But now, since the information in the shuffled layer has already been mixed, we essentially feed each group in GConv2 with different subgroups in the feature map layer (or in the input layer). As a result, we allow the information flow between channels groups and strengthen the representations.

12. 逐点分组卷积Pointwise Grouped Convolution

The ShuffleNet paper also introduced the pointwise grouped convolution. Typically for grouped convolution such as in MobileNet or ResNeXt, the group operation is performed on the 3x3 spatial convolution, but not on 1 x 1 convolution.

The shuffleNet paper argues that the 1 x 1 convolution are also computationally costly. It suggests applying group convolution for 1 x 1 convolution as well. The pointwise grouped convolution, as the name suggested, performs group operations for 1 x 1 convolution. The operation is identical as for grouped convolution, with only one modification — performing on 1x1 filters instead of NxN filters (N>1).

In the ShuffleNet paper, authors utilized three types of convolutions we have learned: (1) shuffled grouped convolution; (2) pointwise grouped convolution; and (3) depthwise separable convolution. Such architecture design significantly reduces the computation cost while maintaining the accuracy. For examples the classification error of ShuffleNet and AlexNet is comparable on actual mobile devices. However, the computation cost has been dramatically reduced from 720 MFLOPs in AlexNet down to 40–140 MFLOPs in ShuffleNet. With relatively small computation cost and good model performance, ShuffleNet gained popularity in the field of convolutional neural net for mobile devices.

13. 动态卷积Dynamic Convolution

请参考我的另一篇博客：Dynamic Convolution: Attention over Convolution Kernels

代码实现(Pytorch)

持续更新中

在这里插入代码片

参考文献

• A Comprehensive Introduction to Different Types of Convolutions in Deep Learning
• A Tutorial on Filter Groups (Grouped Convolution)