2.2 数据结构之 队列与BFS (C语言版）

编程总结

在刷题之前需要反复练习的编程技巧，尤其是手写各类数据结构实现，它们好比就是全真教的上乘武功。

本学习来自 leetcode，整理提炼.
https://leetcode-cn.com/leetbook/read/queue-stack/kyozi/

广度优先搜索（BFS）是一种遍历或搜索数据结构（如树或图）的算法。
如前所述，我们可以使用 BFS 在树中执行层序遍历。
我们也可以使用 BFS 遍历图。例如，我们可以使用 BFS 找到从起始结点到目标结点的路径，特别是最短路径。
我们可以在更抽象的情景中使用 BFS 遍历所有可能的状态。在这种情况下，我们可以把状态看作是图中的结点，而以合法的过渡路径作为图中的边。

1. 解释队列和BFS的关系.

广度优先搜索（BFS）的一个常见应用是找出从根结点到目标结点的最短路径。
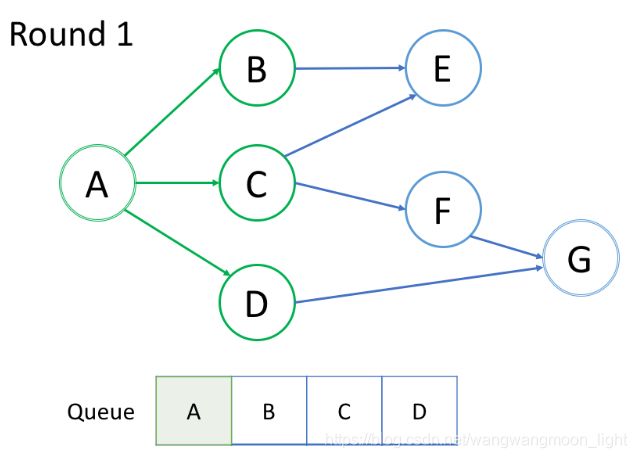
这里我们提供一个示例来说明如何使用 BFS 来找出根结点 A 和目标结点 G 之间的最短路径。

1. 结点的处理顺序是什么？
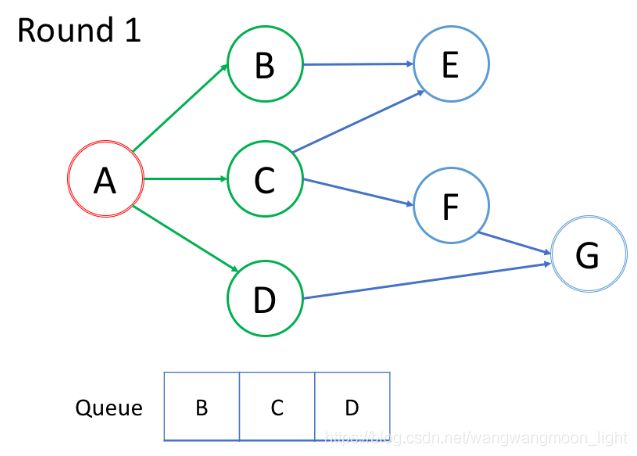
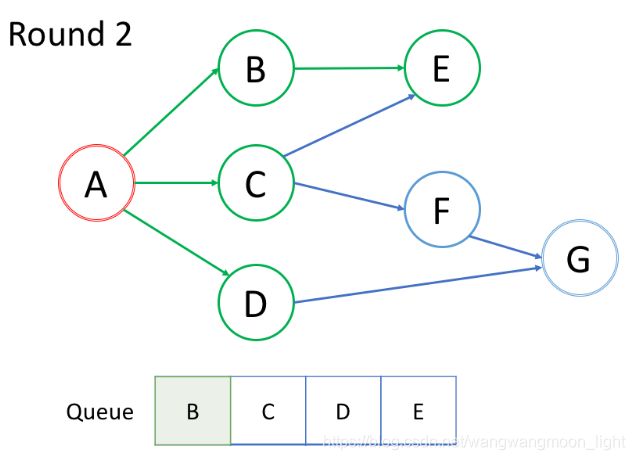
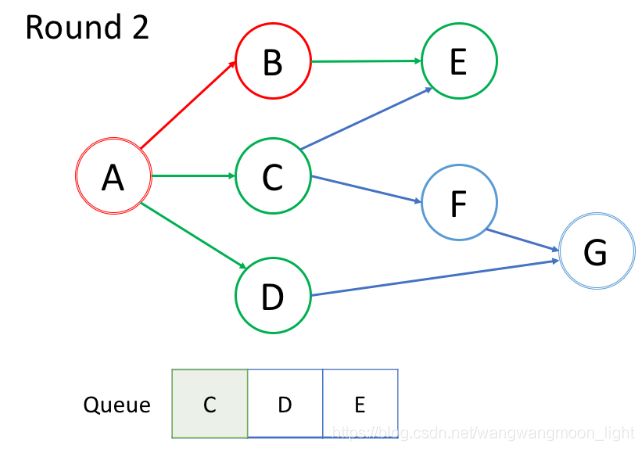
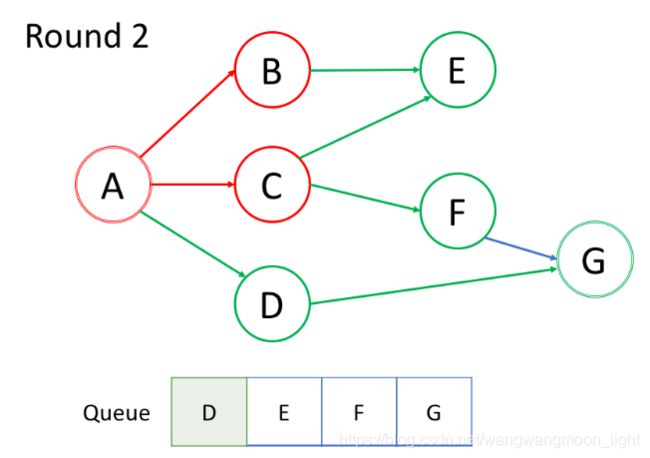
   在第一轮中，我们处理根结点。在第二轮中，我们处理根结点旁边的结点；在第三轮中，我们处理距根结点两步的结点；等等等等。
   与树的层序遍历类似，越是接近根结点的结点将越早地遍历。

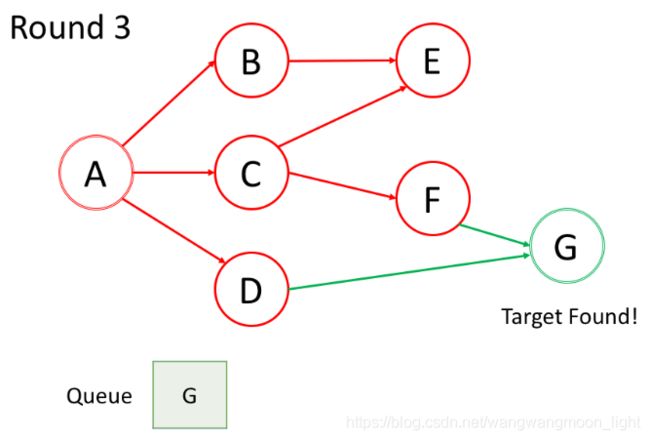
如果在第 k 轮中将结点 X 添加到队列中，则根结点与 X 之间的最短路径的长度恰好是 k。也就是说，第一次找到目标结点时，你已经处于最短路径中。

2. 队列的入队和出队顺序是什么？
   如上面的动画所示，我们首先将根结点排入队列。然后在每一轮中，我们逐个处理已经在队列中的结点，并将所有邻居添加到队列中。值得注意的是，新添加的节点不会立即遍历，而是在下一轮中处理。

结点的处理顺序与它们添加到队列的顺序是完全相同的顺序，即先进先出（FIFO）。这就是我们在 BFS 中使用队列的原因。

广度优先搜索 - 模板

之前，我们已经介绍了使用 BFS 的两个主要方案：遍历或找出最短路径。通常，这发生在树或图中。正如我们在章节描述中提到的，BFS 也可以用于更抽象的场景中。在本文中，我们将为你提供一个模板。然后，我们在本文后提供一些习题供你练习。在特定问题中执行 BFS 之前确定结点和边缘非常重要。通常，结点将是实际结点或是状态，而边缘将是实际边缘或可能的转换。

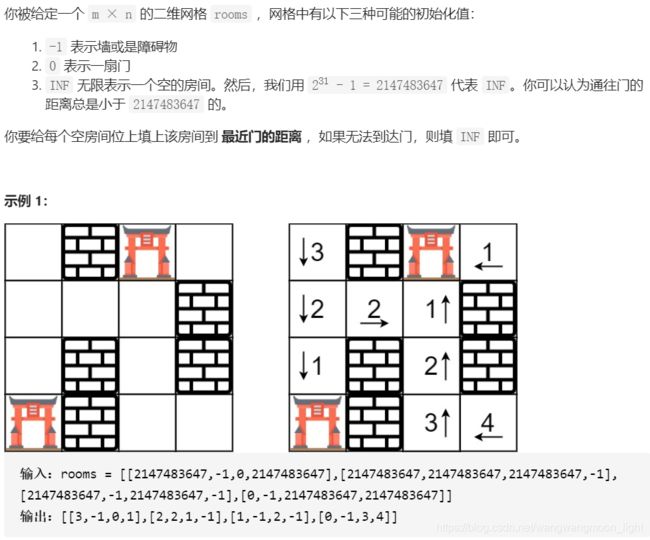
286. 墙与门

// 反向思维，从门开始找
// 反向思维，从门开始找
typedef struct {
     
	int x;
	int y;
	int step;
} Node;

void wallsAndGates(int **rooms, int roomsSize, int *roomsColSize) 
{
     
	if ((roomsSize == 0) || (*roomsColSize == 0)) {
     
		return;
	}
	int row = roomsSize;
	int col = roomsColSize[0];
	int step[4][2] = {
      {
     1,0},{
     -1,0},{
     0,1},{
     0,-1} }; // 下上右左
	Node *queue = (Node *)malloc(sizeof(Node) * row * col);
	int head = 0;
	int tail = 0;
	int i, j;

	// 找门，门节点都入队列.
	for (i = 0; i < row; i++) {
     
		for (j = 0; j < col; j++) {
     
			if (rooms[i][j] == 0) {
     
				queue[tail].x = i;
				queue[tail].y = j;
				queue[tail++].step = 0;
			}
		}
	}
	// 以门为起点开始BFS，利用该门节点遍历所有“岛”节点（这里借助了第200题岛的概念）
	// 循环迭代直到队列为空
	while (tail != head) {
     
		int xx = queue[head].x;
		int yy = queue[head].y;
		int curStep = queue[head++].step; // 门节点出队列
		for (i = 0; i < 4; i++) {
     
			int xNext = xx + step[i][0];
			int yNext = yy + step[i][1];
			if ((xNext >= 0) && (xNext < row) && (yNext >= 0) && (yNext < col) && (rooms[xNext][yNext] == INT_MAX)) {
     
				rooms[xNext][yNext] = curStep + 1;    							 
				queue[tail].x = xNext;
				queue[tail].y = yNext;
				queue[tail++].step = curStep + 1;     // 将当前出队的元素相邻元素入队 
			}
		}
	}
}

200. 岛屿数量

BFS : 思路是线性扫描整个二维网络，如果一个节点包含1，则以其为根节点启动BFS. 并将其设为2(FLAG_NUM)以标记访问过该节点，迭代地搜索队列中的每一个节点，直到队列为空 – 凡是能遍历到的都是一个岛上的. 继续此方法遍历二维网络其他点找其他岛，遍历完后就能找到所有“岛”的数量

#include 
#include 
#include  
#include 

#define FLAG_NUM  2
typedef struct node {
     
	int x;
	int y;
} Node;

// BFS : 思路是线性扫描整个二维网络，如果一个节点包含1，则以其为根节点启动BFS.
// 并将其设为2(FLAG_NUM)以标记访问过该节点，迭代地搜索队列中的每一个节点，直到队列为空 -- 凡是能遍历到的都是一个岛上的.
// 继续此方法遍历二维网络其他点找其他岛，遍历完后就能找到所有“岛”的数量
void BFS(char **grid, int gridSize, int *gridColSize, int i, int j, int flag)
{
     
	Node *queue = (Node *)malloc((gridSize*(gridColSize[0]) + 1) * sizeof(Node));
	Node tmp;
	int step[4][2] = {
     {
     1,0},{
     -1,0},{
     0,1},{
     0,-1}}; // 下上右左
	int head = 0;
	int tail = 0;
	tmp.x = i;
	tmp.y = j;
	queue[tail++] = tmp;                // 首元素入队列

	// 循环迭代直到队列为空
	while (tail != head) {
     
		int x = queue[head].x;
		int y = queue[head++].y;        // 当前点，出队列
		for (int i = 0; i < 4; i++) {
     
			int xNext = x + step[i][0];
			int yNext = y + step[i][1]; // 遍历四个点
			// 有符合条件的元素则加入队列
 			if (xNext >= 0 && xNext < gridSize && yNext >= 0 && yNext < gridColSize[0] && grid[xNext][yNext] == '1') {
     
				grid[xNext][yNext] = '0' + flag;
				tmp.x = xNext;
				tmp.y = yNext;
				queue[tail++] = tmp;   // 入队列
			}
		}
	}
}

int numIslands(char **grid, int gridSize, int *gridColSize) 
{
     
	int flag = FLAG_NUM;
	int result = 0;

	for (int i = 0; i < gridSize; i++) {
     
		for (int j = 0; j < gridColSize[0]; j++) {
     
			if (grid[i][j] == '1') {
     
				BFS(grid, gridSize, gridColSize, i, j, flag);
				result++;
			}
		}
	}

	return result;
}

int main(void)
{
     
	char **grid =  NULL;
	int gridSize = 4;
	int gridColSize = 5;

	grid = (char **)malloc(sizeof(char *));
	for (int i = 0; i < 4; i++) {
     
		grid[i] = (char *)malloc(sizeof(char)*5);
	}
	grid[0][0] = '1';
	grid[0][1] = '1';
	grid[0][2] = '1';
	grid[0][3] = '1';
	grid[0][4] = '0';
	grid[1][0] = '1';
	grid[1][1] = '1';
	grid[1][2] = '0';
	grid[1][3] = '1';
	grid[1][4] = '0';
	grid[2][0] = '1';
	grid[2][1] = '1';
	grid[2][2] = '0';
	grid[2][3] = '0';
	grid[2][4] = '0';
	grid[3][0] = '0';
	grid[3][1] = '0';
	grid[3][2] = '0';
	grid[3][3] = '0';
	grid[3][4] = '0';

	numIslands(grid, gridSize, &gridColSize);

	return 0;
}

752.打开转盘锁

#include 
#include 
#include  
#include 

#define KEY_LENTH 4
#define QUEUE_LENTH 10000

typedef struct {
     
	char key[KEY_LENTH + 1];
} Node;

// 构造循环队列
typedef struct {
     
	Node *base;
	int head;
	int tail;
	int MaxSize;
} Queue;

Queue *QueueCreate(int k)
{
     
	Queue *obj = (Queue *)malloc(sizeof(Queue));
	if (obj == NULL) {
     
		return NULL;
	}
	obj->base = (Node *)malloc(sizeof(Node) * (k + 1));
	memset(obj->base, 0, sizeof(Node) * (k + 1));
	obj->head = 0;
	obj->tail = 0;
	obj->MaxSize = k + 1;

	return obj;
}

bool QueueIsEmpty(Queue  *obj)
{
     
	if (obj->head == obj->tail) {
     
		return true;
	}

	return false;
}

bool QueueIsFull(Queue *obj)
{
     
	return ((obj->tail + 1) == obj->head);
}

bool QueueEnQueue(Queue *obj, Node value)
{
     
	if (QueueIsFull(obj) == true) {
     
		return false;
	}

	obj->base[obj->tail] = value;
	obj->tail = (obj->tail + 1) % obj->MaxSize;
	return true;
}

bool QueueDeQueue(Queue *obj)
{
     
	if (QueueIsEmpty(obj) == true) {
     
		return false;
	}

	obj->head = (obj->head + 1) % obj->MaxSize;
	return true;
}

Node QueueFront(Queue *obj)
{
     
	return obj->base[obj->head];
}

Node QueueTail(Queue *obj)
{
     
	return obj->base[(obj->tail - 1)];
}

int QueueSize(Queue *obj)
{
     
	if (obj->head > obj->tail) {
     
		return obj->tail + obj->MaxSize - obj->head;
	}
	return obj->tail - obj->head;
}

void QueueFree(Queue *obj)
{
     
	if (obj->base) {
     
		free(obj->base);
	}
	obj->base = NULL;     // 先释放指针，并赋值NULL
	obj->head = 0;
	obj->tail = 0;
	free(obj);
}

//* -----------------------------  *//

Queue *gQueue;
int    gVisited[QUEUE_LENTH];

int Str2Int(char *s, int len)
{
     
	int ret = 0;
	for (int i = 0; i < len; i++) {
     
		ret = ret * 10;
		ret = ret + s[i] - '0';
	}

	return ret;
}

bool IsTarget(char *str, char *target)
{
     
	return !strcmp(str, target);
}

void InitVisitDead(char **deadends, int deadendsSize)
{
     
	for (int i = 0; i < deadendsSize; i++) {
     
		int index = atoi(deadends[i]);
		gVisited[index] = 1;
	}
}

bool isInDead(char *str, char **deadends, int deadendsSize)
{
     
	for (int i = 0; i < deadendsSize; i++) {
     
		if (IsTarget(str, deadends[i]) == true) {
     
			return true;
		}
	}

	return false;
}

void GetNextNodeEnQueue(Queue *obj, char *str, char **deadends, int deadendsSize)
{
     
	/* 基于当前数字产生新的8位数字（各个位置前后旋转） */
	for (int i = 0; i < KEY_LENTH; i++) {
     
		for (int step = -1; step <= 1; step += 2) {
     
			char nextCode[KEY_LENTH + 1];
			memcpy(nextCode, str, 5);
			nextCode[KEY_LENTH] = '\0';
			nextCode[i] = (nextCode[i] - '0' + step + 10) % 10 + '0';
			int index = atoi(nextCode);

			if (isInDead(nextCode, deadends, deadendsSize) == true || gVisited[index] == 1) {
     
				continue;
			}

			Node enNode;
			memcpy(enNode.key, nextCode, 5);
			QueueEnQueue(gQueue, enNode);
			gVisited[index] = 1;
		}
	}
}

int openLock(char **deadends, int deadendsSize, char *target)
{
     
	int steps = 0;
	char *str = (char *)"0000";

	if (isInDead(str, deadends, deadendsSize) == true) {
     
		return -1;
	}
	gQueue = QueueCreate(QUEUE_LENTH);
	memset(gVisited, 0, QUEUE_LENTH * sizeof(int));
	InitVisitDead(deadends, deadendsSize);

	// 将起点"0000"入队列  
	Node enNode;
	memcpy(enNode.key, str, 5);
	QueueEnQueue(gQueue, enNode);
	gVisited[0] = 1;

	if (strcmp(str, target) == 0) {
     
		return 0;
	}

	// 遍历队列  
	while (QueueIsEmpty(gQueue) == false) {
     
		steps++;
		int queueSize = QueueSize(gQueue);
		for (int i = 0; i < queueSize; i++) {
      // 遍历已在队列中的节点 
			Node deNode;
			deNode = QueueFront(gQueue);
			QueueDeQueue(gQueue);
			// 获取当前值的邻接值，判断是否在黑名单中，如不在，入队列 
			// 基于当前数字产生新的8位数字（各个位置前后旋转） 
			for (int i = 0; i < KEY_LENTH; i++) {
     
				for (int step = -1; step <= 1; step += 2) {
     
					char nextCode[KEY_LENTH + 1];
					memcpy(nextCode, deNode.key, 5);
					nextCode[KEY_LENTH] = '\0';
					nextCode[i] = (nextCode[i] - '0' + step + 10) % 10 + '0'; // 这个手法的处理也是可以
					int index = atoi(nextCode);
					if (IsTarget(nextCode, target) == true) {
     
						return steps;
					}
					if (gVisited[index] == 1) {
     
						continue;
					}
					Node enNode;                     // 建立新的结点并入队列
					memcpy(enNode.key, nextCode, 5); 
					QueueEnQueue(gQueue, enNode);
					gVisited[index] = 1;
				}
			}
		}
	}
	QueueFree(gQueue);
	return -1;
}


int main(void)
{
     
	char **deadends =(char **)malloc(sizeof(char *) * 5);
	char *target = (char *)"0000";
	int  deadendsSize = 4;

	for (int i = 0; i < 5; i++) {
     
		deadends[i] = (char *)malloc(sizeof(char)*5);
	}
	memcpy(deadends[0], "0201", 5);
	memcpy(deadends[1], "0101", 5);
	memcpy(deadends[2], "0102", 5);
	memcpy(deadends[3], "1212", 5);
	memcpy(deadends[4], "2002", 5);
	openLock(deadends, deadendsSize, target);

	return 0;
}