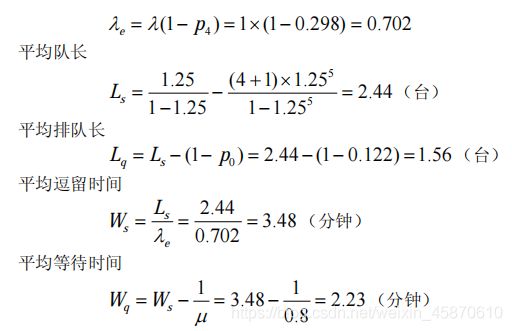排队论模型

一、为什么需要有排队论模型

• 在服务过程中，要求服务的数量超过了服务机构（服务台，服务 员等）的容量，客户不能离地得到服务，因而产 生了排队现象。
• 常见于旅客购票排队、市内电话占线问题、车，船堵塞和疏导，故障及其停机待修，水库的存储调节等等，由于顾客到达和服务时间的随机性，排队现象机会是不可避免的。

二、排队论的定义

排队论是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，又称随机服务系统理论，为运筹学的一个分支。

如下为排队论的随机服务系统理论：

三、排队论的一般模型和研究目的

• 排队论的一般模型，要求服务的对象：顾客，为 顾客服务的人：服务员。

• 研究排队模型的目的：在顾客需要和服务机构的 规模之间进行权衡决策，使其达到合理的平衡。

四、排队系统的组成和特征

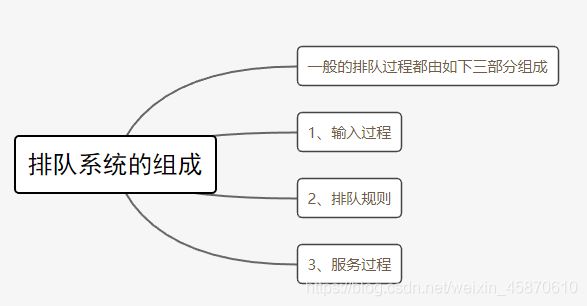
4.1排队系统的组成

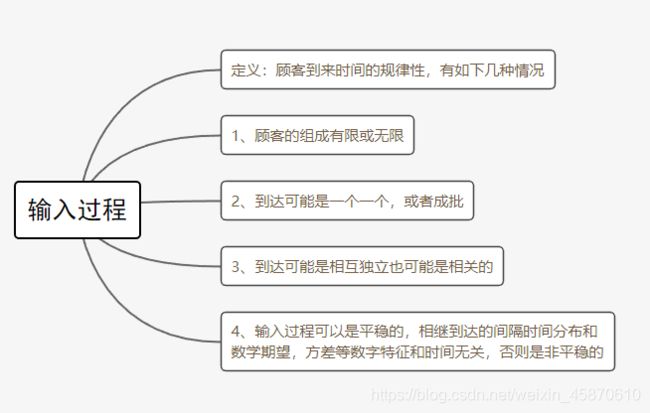
4.1.1输入过程

4.1.2排队规则

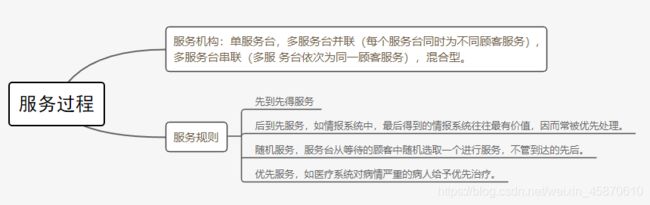
4.1.3服务过程

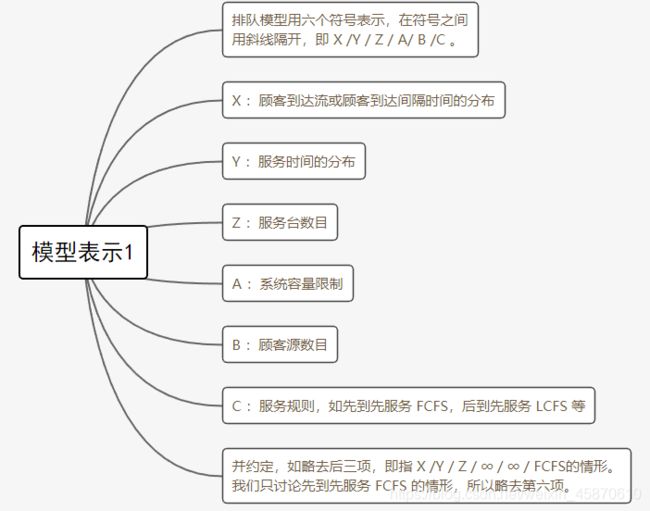
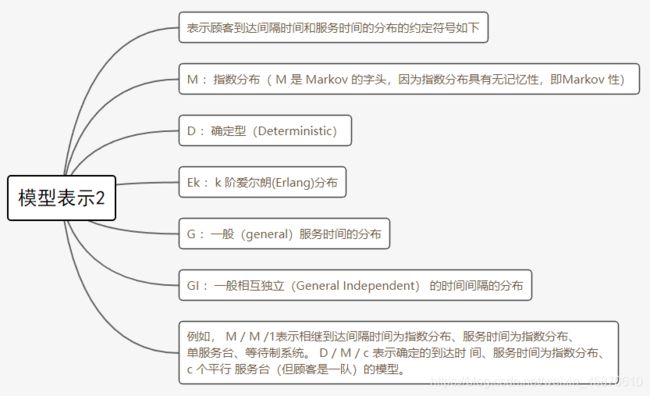
4.2排队论模型表示

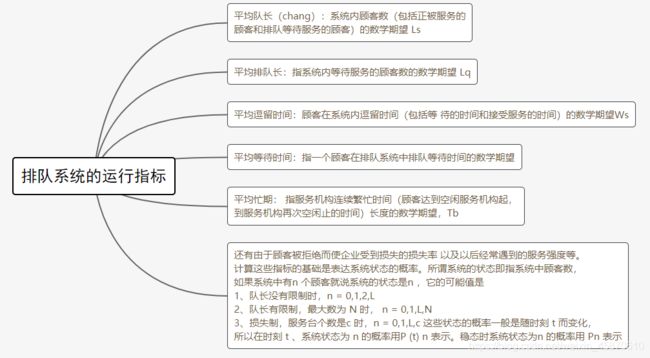
4.3排队系统的运行指标

4.4输入过程和服务时间的分布

排队系统中的事件流包括顾客到达流和服务时间流。由于顾客到达的间隔时间和服务时间不可能是负值，因此，它的分布是非负随机变量的分布。最常用的分布有泊松分布、确定型分布，指数分布和爱尔朗分布。

当输入过程是泊松流时，那么顾客相继到达的时间间隔T必服从指数分布。

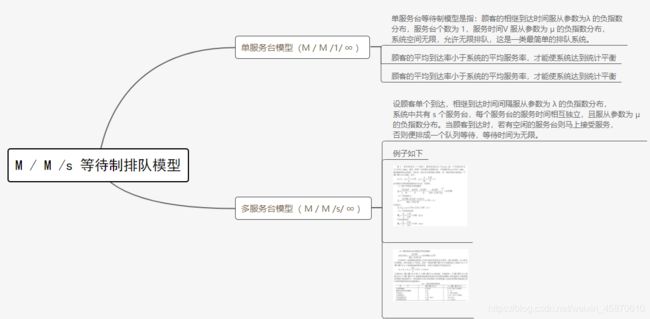
五、M / M /s 等待制排队模型

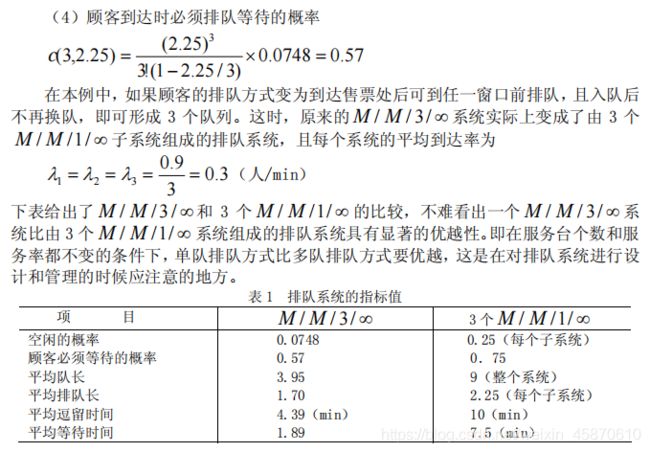
如下是上图中的例子

六、M / M / s/ s 损失制排队模型

当 s 个服务台被占用后，顾客自动离去。

6.1 损失制排队模型的基本参数

对于损失制排队模型，其模型的基本参数与等待制排队模型有些不同，我们关心如下指标：


在上述公式中，引入λe 是十分重要的，因为尽管顾客以平均λ 的速率到达服务系统，但当系统被占满后，有一部分顾客会自动离去，因此，真正进入系统的顾客输入率
是λe ，它小于λ 。

6.2损失制排队模型计算实例

6.2.1 s =1的情况（ M / M /1/1）

例 3 设某条电话线，平均每分钟有 0.6 次呼唤，若每次通话时间平均为 1.25min，求系统相应的参数指标。
解：其参数为 s＝1，λ = 0.6， μ = 1/1.25

编写lingo程序如下：

model: 
s=1;lamda=0.6;mu=1/1.25;rho=lamda/mu; 
Plost=@pel(rho,s); 
Q=1-Plost; 
lamda_e=Q*lamda;A=Q*lamda_e; 
L_s=lamda_e/mu; 
eta=L_s/s; 
end

6.2.2 s >1的情况（ M / M / s/ s ）

例4 某单位电话交换台有一台200门内线的总机，已知在上班8h的时间内，有20％的内线分机平均每40min要一次外线电话，80％的分机平均隔120min要一次外线。又知外线打入内线的电话平均每分钟1次。假设与外线通话的时间平均为3min，并且上述时间均服从负指数分布，如果要求电话的通话率为95％，问该交换台应设置多少条外线？

以下是lingo程序：

model: 
lamda=200; 
mu=60/3;rho=lamda/mu; 
Plost=@pel(rho,s);Plost<0.05; 
Q=1-Plost; 
lamda_e=Q*lamda;A=Q*lamda_e; 
L_s=lamda_e/mu; 
eta=L_s/s; 
min=s;@gin(s); 
end

求得需要15条外线。在此条件下，交换台的顾客损失率为3.65％，有96.35％的电话得到了服务，通话率为平均每小时185.67次，交换台每条外线的服务效率为64.23％。
求解时，尽量选用简单的模型让LINGO软件求解，而上述程序是解非线性整数规划（尽管是一维的），但计算时间可能会较长，因此，我们选用下面的处理方法，分两步处理。

• 第一步，求出概率为5％的服务台的个数，尽管要求服务台的个数是整数，但@pel给出的是实数解。以下是lingo程序：

model: 
lamda=200; 
mu=60/3;rho=lamda/mu; 
@pel(rho,s)=0.05; 
end

求得 s =14.33555

• 第二步，注意到@pel(rho,s)是s的单调递减函数，因此，对s取整数（采用只入不舍原则）就是满足条件的最小服务台数，然后再计算出其它的参数指标。以下是lingo程序：

model: 
lamda=200; 
mu=60/3;rho=lamda/mu; 
s=15;Plost=@pel(rho,s); 
Q=1-Plost; 
lamda_e=Q*lamda;A=Q*lamda_e; 
L_s=lamda_e/mu; 
eta=L_s/s; 
end

比较上面两种方法的计算结果，其答案是相同的，但第二种方法比第一种方法在计算时间上要少许多。

七、M / M / s 混合制排队模型

7.1单服务台混合制模型

单服务台混合制模型 M / M /1/ K 是指：顾客的相继到达时间服从参数为λ 的负指数分布，服务台个数为1，服务时间V 服从参数为 μ 的负指数分布，系统的空间为 K ，当 K个位置已被顾客占用时，新到的顾客自动离去，当系统中有空位置时，新到的顾客进入系统排队等待。

以下是lingo程序：

model: 
sets: 
state/1..4/:p; 
endsets 
lamda=1;mu=1/1.25;rho=lamda/mu;k=4; 
lamda*p0=mu*p(1); 
(lamda+mu)*p(1)=lamda*p0+mu*p(2); 
@for(state(i)|i #gt#1 #and# i #lt# 
k:(lamda+mu)*p(i)=lamda*p(i-1)+mu*p(i+1)); 
lamda*p(k-1)=mu*p(k); 
p0+@sum(state:p)=1; 
P_lost=p(k);lamda_e=lamda*(1-P_lost); 
L_s=@sum(state(i)|i #le#k:i*p(i)); 
L_q=L_s-(1-p0); 
W_s=L_s/lamda_e; 
W_q=W_s-1/mu; 
end

7.2多服务台混合制模型

多服务台混合制模型 M / M / s/ K 是指顾客的相继到达时间服从参数为λ 的负指数分布，服务台个数为 s ，每个服务台服务时间相互独立，且服从参数为 μ 的负指数分布，系统的空间为 K 。

lingo求解程序

model: 
sets: 
state/1..5/:p; 
endsets 
lamda=2;mu=0.5;rho=lamda/mu;s=2;k=5; 
lamda*p0=mu*p(1); 
(lamda+mu)*p(1)=lamda*p0+2*mu*p(2); 
@for(state(i)|i #gt#1 #and# i #lt# s: 
(lamda+i*mu)*p(i)=lamda*p(i-1)+(i+1)*mu*p(i+1)); 
@for(state(i)|i #ge# s #and# i #lt# k: 
(lamda+s*mu)*p(i)=lamda*p(i-1)+s*mu*p(i+1)); 
lamda*p(k-1)=s*mu*p(k); 
p0+@sum(state:p)=1; 
P_lost=p(k);lamda_e=lamda*(1-P_lost); 
L_s=@sum(state(i):i*p(i)); 
L_q=L_s-lamda_e/mu; 
W_s=L_s/lamda_e; 
W_q=W_s-1/mu; 
end

八、其它排队模型简介

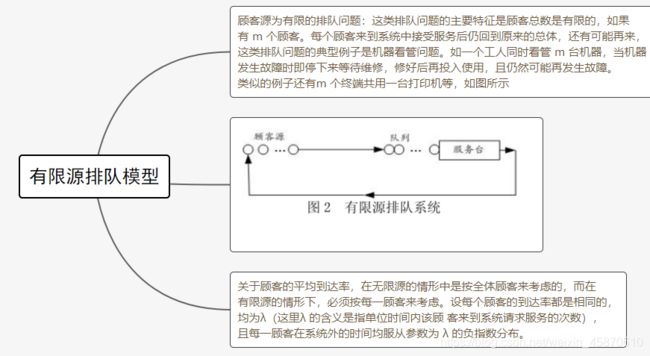
8.1有限源排队模型

model: 
lamda=1/15;mu=1/12;rho=lamda/mu;s=1;m=5; 
load=m*rho; 
L_s=@pfs(load,s,m); 
p_0=1-(m-L_s)*rho; 
lamda_e=lamda*(m-L_s); 
p_5=@exp(@lgm(6))*0.8^5*p_0; 
L_q=L_s-(1-p_0); 
w_s=L_s/lamda_e;w_q=L_q/lamda_e; 
end

8.2服务率或到达率依赖状态的排队模型

• 在前面的各类排队模型的分析中，均假设顾客的到达率为常数 λ ，服务台的服务率也为常数 μ 。 而在实际的排队问题中，到达率或服务率可能是随系统的状态而变化的。

• 例如，当系统中顾客数 已经比较多时，后来的顾客可能不愿意再进入系统；服务员的服务率当顾客较多时也可能会提高。

8.3非生灭过程排队模型

• 一个排队系统的特征是由输入过程，服务机制和队规则决定的。
  本文章前面所讨论的排队模型都是输入过程为 Poisson 流，服务时间服从负指数分布的生灭过程排队模型。
• 这类排队系统的一个主要特征是马尔可夫性，而马尔可夫性的一个主要性质是由系统当前的状态可以推断未来的状态。
  但是，当输入过程不是 Poisson 流或服务时间不服从负指数分布时，仅知道系统内当前的顾客数，对于推断系统未来的状态是不充足的， 因为正在接受服务的顾客，已经被服务了多长时间，将影响其离开系统的时间。因此，必须引入新的方法来分析具有非负指数分布的排队系统。

九、排队系统的优化

静态优化，即在服务系统设置以前根据一定的质量指标，找出参数的最优值，从而使系统最为经济。 动态优化，即对已有的排队系统寻求使其某一目标函数达到最优的运营机制。