小白python学习——机器学习篇——k-近邻算法（KNN算法）

一、算法理解

一般给你一数据集，作为该题目的数据（一个矩阵，每一行是所有特征），而且每一组数据都是分了类，然后给你一个数据，让这个你预测这组数据属于什么类别。你需要对数据集进行处理，如：归一化数值。处理后可以用matplotlib绘制出图像，一般选两个特征绘制x，y轴，然后核心是计算出预测点到各个数据的距离，距离越小越接近正确。选出整个统计数据集的k个，然后概率大的一类作为该数据的分类。

二、步骤简介

1、收集数据，把数据从文件中合理提取出来，会用到一个提取数据函数。

2.分析数据，使用matplotlib绘制整体分布，记住选出两个特征作为x，y值

3.准备数据（数据处理），数据归一化，使数据变成在【-1,1】之间，公式：newValue=（oldvalue-min）/（max-min）

这里的max和min是每一列的最值，也就是所有个体的同一特征。

4.实现算法，通过矩阵在坐标轴的距离，实现分类

5.算法错误率的计算（这里不说了）

三、算法展示

1.收集数据：

def file2matrix(filename):
    # 打开文件
    fr = open(filename)
    # 计算文本文件的行数
    numberOfLines = len(fr.readlines())
    # 创建返回的数据矩阵
    returnMat = np.zeros((numberOfLines,3))
    # 创建类标签
    classLabelVector = []
    # 打开文件
    fr = open(filename)
    # 定义索引
    index = 0
    # 读取文件的每一行并处理
    for line in fr.readlines():
        # 去除行的尾部的换行符
        line = line.strip()
        # 将一行数据按空进行分割
        listFromLine = line.split('\t')
        # 0：3列为数据集的数据
        returnMat[index,:] = listFromLine[0:3]
        # 最后一列为数据的分类标签
        classLabelVector.append(listFromLine[-1])
        # 索引加1
        index += 1
    # 返回数据集和对应的类标签
    return returnMat,classLabelVector

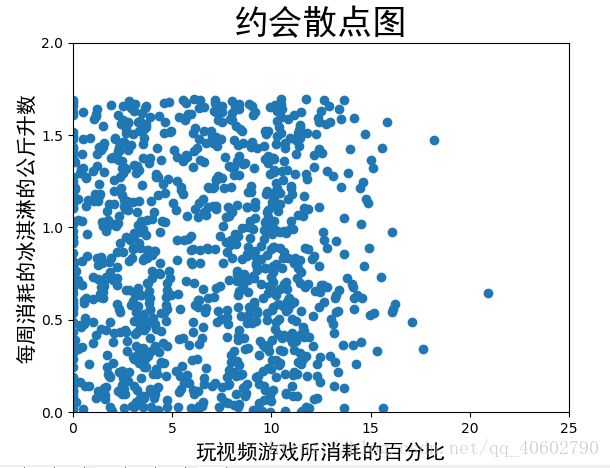
      2.分析数据（matplotlib实现散点图）

def scatter(returnMat):
    plt.scatter(returnMat[:, 1], returnMat[:, 2])
    plt.title("约会散点图", fontproperties="SimHei", fontsize=25)
    plt.xlabel("玩视频游戏所消耗的百分比", fontproperties="SimHei", fontsize=15)
    plt.ylabel("每周消耗的冰淇淋的公斤升数", fontproperties="SimHei", fontsize=15)
    plt.xlim((0, 25))
    plt.ylim((0.0, 2.0))
    plt.xticks([0, 5, 10, 15, 20, 25])
    plt.yticks([0.0, 0.5, 1.0, 1.5, 2.0])
    plt.show()
#绘制数据集的散点图

效果图：

3.数据处理（归一化数值）.

def autoNorm(dataSet):
    # 求数据矩阵每一列的最小值
    minVals = dataSet.min(0)
    # 求数据矩阵每一列的最大值
    maxVals = dataSet.max(0)
    # 求数据矩阵每一列的最大最小值差值
    ranges = maxVals - minVals
    #    normDataSet = zeros(shape(dataSet))
    # 返回数据矩阵第一维的数目
    m = dataSet.shape[0]
    # 求矩阵每一列减去该列最小值，得出差值
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    # 用求的差值除以最大最小值差值，即数据的变化范围，即归一化
    normDataSet = normDataSet / np.tile(ranges, (m, 1))
    # 返回归一化后的数据，最大最小值差值，最小值
    return normDataSet, ranges, minVals
#将数据集归一化特征值

归一化前后图：

[[4.0920000e+04 8.3269760e+00 9.5395200e-01]                                        
 [1.4488000e+04 7.1534690e+00 1.6739040e+00]
 [2.6052000e+04 1.4418710e+00 8.0512400e-01]
 ...
 [2.6575000e+04 1.0650102e+01 8.6662700e-01]
 [4.8111000e+04 9.1345280e+00 7.2804500e-01]
 [4.3757000e+04 7.8826010e+00 1.3324460e+00]]                

 

[[0.44832535 0.39805139 0.56233353]
 [0.15873259 0.34195467 0.98724416]
 [0.28542943 0.06892523 0.47449629]
 ...
 [0.29115949 0.50910294 0.51079493]
 [0.52711097 0.43665451 0.4290048 ]
 [0.47940793 0.3768091  0.78571804]]      

 

4.实现算法

def autoNorm(dataSet):
    # 求数据矩阵每一列的最小值
    minVals = dataSet.min(0)
    # 求数据矩阵每一列的最大值
    maxVals = dataSet.max(0)
    # 求数据矩阵每一列的最大最小值差值
    ranges = maxVals - minVals
    #    normDataSet = zeros(shape(dataSet))
    # 返回数据矩阵第一维的数目
    m = dataSet.shape[0]
    # 求矩阵每一列减去该列最小值，得出差值
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    # 用求的差值除以最大最小值差值，即数据的变化范围，即归一化
    normDataSet = normDataSet / np.tile(ranges, (m, 1))
    # 返回归一化后的数据，最大最小值差值，最小值
    return normDataSet, ranges, minVals
#将数据集归一化特征值

注解：数据来源来自《机器学习实战》 ——Peter Harrington 著