机器学习训练_金融风控_Task5_模型融合

序

模型融合是比赛后期上分的重要手段，特别是多人组队学习的比赛中，将不同队友的模型进行融合，可能会收获意想不到的效果哦，往往模型相差越大且模型表现都不错的前提下，模型融合后结果会有大幅提升。

# 简单加权平均-结果直接融合

'''
生成一些简单的样本数据,
test_prei - 代表第i个模型的预测值
y_test_true - 代表真实值
'''
test_pre1 = [1.2, 3.2, 2.1, 6.2]
test_pre2 = [0.9, 3.1, 2.0, 5.9]
test_pre3 = [1.1, 2.9, 2.2, 6.0]
y_test_true = [1, 3, 2, 6]

# 定义结果的加权平均函数 - 根据加权计算

def weighted_method(test_pre1, test_pre2, test_pre3, w=[1/3, 1/3, 1/3]):
    weighted_result = w[0] * pd.Series(test_pre1) + w[1] * pd.Series(test_pre2) + w[2] * pd.Series(test_pre3)
    return weighted_result

# 根据各模型的预测结果计算MAE

'''
metrics.mean_absolute_error - 多维数组MAE的计算方法
'''
print('Pred1 MAE:', metrics.mean_absolute_error(y_test_true, test_pre1))
print('Pred2 MAE:', metrics.mean_absolute_error(y_test_true, test_pre2))
print('Pred3 MAE:', metrics.mean_absolute_error(y_test_true, test_pre3))

Pred1 MAE: 0.1750000000000001
Pred2 MAE: 0.07499999999999993
Pred3 MAE: 0.10000000000000009

# 根据加权计算MAE

## 定义比重权值

w = [0.3, 0.4, 0.3]
weighted_pre = weighted_method(test_pre1, test_pre2, test_pre3, w)
print('Weighted_pre MAE:', metrics.mean_absolute_error(y_test_true, weighted_pre))

Weighted_pre MAE: 0.05750000000000027

# 定义结果的加权平均函数 - mean平均

def mean_method(test_pre1, test_pre2, test_pre3):
    mean_result = pd.concat([pd.Series(test_pre1),
                             pd.Series(test_pre2),
                             pd.Series(test_pre3)], axis=1).mean(axis=1)
    return mean_result

# 根据均值计算MAE

Mean_pre = mean_method(test_pre1, test_pre2, test_pre3)
print('Mean_pre MAE:', metrics.mean_absolute_error(y_test_true, Mean_pre))


Mean_pre MAE: 0.06666666666666693

# 定义结果的加权平均函数 - median平均

def median_method(test_pre1, test_pre2, test_pre3):
    median_result = pd.concat([pd.Series(test_pre1),
                               pd.Series(test_pre2),
                               pd.Series(test_pre3)], axis=1).median(axis=1)
    return median_result

# 根据中位数计算MAE

Median_pre = median_method(test_pre1, test_pre2, test_pre3)
print('Median_pre MAE:', metrics.mean_absolute_error(y_test_true, Median_pre))


Median_pre MAE: 0.07500000000000007

# Stacking融合(回归)

# 定义Stacking融合函数

def Stacking_method(train_reg1, train_reg2, train_reg3,
                    y_train_true,
                    test_pre1, test_pre2, test_pre3,
                    model_L2=linear_model.LinearRegression()):
    '''
    :param train_reg1:  第一个模型预测train得到的标签
    :param train_reg2:  第二个模型预测train得到的标签
    :param train_reg3:  第三个模型预测train得到的标签
    :param y_train_true:    train真实的标签
    :param test_pre1:   第一个模型预测test得到的标签
    :param test_pre2:   第二个模型预测test得到的标签
    :param test_pre3:   第三个模型预测test得到的标签
    :param model_L2:    次级模型:以真实训练集的标签为标签,以多个模型训练训练集后得到的标签合并后的数据集为特征进行训练
                        注意:次级模型不宜选取的太复杂,这样会导致模型在训练集上过拟合,测试集泛化效果差
    :return:            训练好的次机模型预测test数据集得到的预测值 - Stacking_result
    '''
    model_L2.fit(pd.concat([pd.Series(train_reg1), pd.Series(train_reg2), pd.Series(train_reg3)], axis=1).values,
                 y_train_true)      # 次级模型训练
    stacking_result = model_L2.predict(pd.concat([pd.Series(test_pre1),
                                                  pd.Series(test_pre2), pd.Series(test_pre3)], axis=1).values)
    return stacking_result

# 生成一些简单的样本数据,test_prei代表第i个模型的预测值,y_test_true代表模型的真实值

train_reg1 = [3.2, 8.2, 9.1, 5.2]
train_reg2 = [2.9, 8.1, 9.0, 4.9]
train_reg3 = [3.1, 7.9, 9.2, 5.0]
y_train_true = [3, 8, 9, 5]

test_pre1 = [1.2, 3.2, 2.1, 6.2]
test_pre2 = [0.9, 3.1, 2.0, 5.9]
test_pre3 = [1.1, 2.9, 2.2, 6.0]
y_test_true = [1, 3, 2, 6]

# 看一下Stacking融合的效果

model_L2 = linear_model.LinearRegression()      # 不设定这个参数也可以,创建函数的时候默认了
Stacking_pre = Stacking_method(train_reg1, train_reg2, train_reg3, y_train_true,
                               test_pre1, test_pre2, test_pre3, model_L2)
print('Stacking_pre MAE: ', metrics.mean_absolute_error(y_test_true, Stacking_pre))


Stacking_pre MAE:  0.042134831460675204
# 发现模型效果相对于之前有了更近一步的提升

# 分类模型融合 - Voting,Stacking…

# Voting投票机制

'''
Voting - 投票机制
        1.硬投票 - 对多个模型直接进行投票,不区分模型结果的相对重要度,最终投票数最多的类为最终被预测的类
        2.软投票 - 和硬投票原理相同,增加了设置权重的功能,可以为不同模型设置不同权重,进而区别模型不同的重要度
'''

# # 硬投票
iris = datasets.load_iris()     # 读取鸢尾花数据集 - 分类问题

x = iris.data   # 分离特征集和标签
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)    # 训练集和测试集按照7:3比例切分

# 用XGB分类模型训练数据

'''
colsample_bytree - 训练每棵树时，使用的特征占全部特征的比例
objective - 目标函数
            二分类问题 - binary:logistic - 返回概率
'''
clf1 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=3, min_child_weight=2, subsample=0.7,
                     colsample_bytree=0.6, objective='binary:logistic')

# 用随机森林分类模型训练数据

'''
n_estimators - 随机森林中决策树的个数
max_depth - 决策树的最大深度
            如果值为None,那么会扩展节点,直到所有的叶子是纯净的,或者直到所有叶子包含少于min_sample_split的样本
min_samples_split - 分割内部节点所需要的最小样本数量
min_samples_leaf - 需要在叶子结点上的最小样本数量
oob_score - 是否使用袋外样本来估计泛化精度
            树的生成过程并不会使用所有的样本,未使用的样本就叫(out_of_bag)oob袋外样本,通过袋外样本,可以评估这个树的准确度
'''
clf2 = RandomForestClassifier(n_estimators=50, max_depth=1, min_samples_split=4,
                              min_samples_leaf=63, oob_score=True)

# 用SVC训练数据

'''
支持向量机 - 分类算法，但是也可以做回归,根据输入的数据不同可做不同的模型
            1.若输入标签为连续值则做回归
            2.若输入标签为分类值则用SVC()做分类
            支持向量机的学习策略是间隔最大化，最终可转化为一个凸二次规划问题的求解

参数详解:
C - 惩罚参数;   值越大,对误分类的惩罚大,不容犯错,于是训练集测试准确率高,但是泛化能力弱
                值越小,对误分类的惩罚小,允许犯错,泛化能力较强
probability - 是否采用概率估计,默认为False
'''
clf3 = SVC(C=0.1)

# 硬投票

'''
eclf - 其实就是三个模型的集成算法,硬投票决定最终被预测的类
'''
eclf = VotingClassifier(estimators=[('xgb', clf1), ('rf', clf2), ('svc', clf3)], voting='hard')     # 本质是Ensemble
for clf, label in zip([clf1, clf2, clf3, eclf], ['XGBBoosting', 'Random Forest', 'SVM', 'Ensemble']):
    scores = cross_val_score(clf, x, y, cv=5, scoring='accuracy')   # 以准确度度量评分
    print('Accuracy: %0.2f (+/- %0.2f) [%s]' % (scores.mean(), scores.std(), label))


Accuracy: 0.96 (+/- 0.02) [XGBBoosting]
Accuracy: 0.33 (+/- 0.00) [Random Forest]
Accuracy: 0.92 (+/- 0.03) [SVM]
Accuracy: 0.95 (+/- 0.05) [Ensemble]

# 软投票

x = iris.data
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

clf1 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=3, min_child_weight=2, subsample=0.8,
                     colsample_bytree=0.8, objective='binary:logistic')
clf2 = RandomForestClassifier(n_estimators=50, max_depth=1, min_samples_split=4,
                              min_samples_leaf=63, oob_score=True)
clf3 = SVC(C=0.1, probability=True)
eclf = VotingClassifier(estimators=[('xgb', clf1), ('rf', clf2), ('svc', clf3)], voting='soft', weights=[2, 1, 1])
for clf, label in zip([clf1, clf2, clf3, eclf], ['XGBBoosting', 'Random Forest', 'SVM', 'Ensemble']):
    scores = cross_val_score(clf, x, y, cv=5, scoring='accuracy')   # 以准确度度量评分
    print('Accuracy: %0.2f (+/- %0.2f) [%s]' % (scores.mean(), scores.std(), label))



Accuracy: 0.96 (+/- 0.02) [XGBBoosting]
Accuracy: 0.33 (+/- 0.00) [Random Forest]
Accuracy: 0.92 (+/- 0.03) [SVM]
Accuracy: 0.96 (+/- 0.02) [Ensemble]

# 分类的Stacking/Blending融合

'''
Stacking是一种分层模型集成框架,以两层为例
        第一层由多个基学习器组成,其输入为原始训练集
        第二层的模型则是以第一层学习器的输出作为训练集进行再训练,从而得到完整的stacking模型
'''
# ## 创建训练用的数据集
data_0 = iris.data
data = data_0[:100, :]  # 100个样本

target_0 = iris.target
target = target_0[:100]

# ## 模型融合中使用到的各个单模型
'''
LogisticRegression()
            solver - 用来优化权重     {‘lbfgs’, ‘sgd’, ‘adam’},默认adam,
                                        lbfgs - quasi-Newton方法的优化器:对小数据集来说,lbfgs收敛更快效果也更好
                                        sgd - 随机梯度下降 
                                        adam - 机遇随机梯度的优化器

RandomForestClassifier()
            n_estimators - 决策树个数
            n_jobs - 用于拟合和预测的并行运行的工作数量,如果值为-1,那么工作数量被设置为核的数量
            criterion - 衡量分裂质量的性能
                        1.gini - Gini impurity衡量的是从一个集合中随机选择一个元素
                                基于该集合中标签的概率分布为元素分配标签的错误率
                                Gini impurity的计算就非常简单了,即1减去所有分类正确的概率,得到的就是分类不正确的概率
                                若元素数量非常多,且所有元素单独属于一个分类时，Gini不纯度达到极小值0
                        2.entropy - 信息增益熵
                        
ExtraTreesClassifier() - 极端随机树
    该算法与随机森林算法十分相似,都是由许多决策树构成,但该算法与随机森林有两点主要的区别:
        1.随机森林应用的是Bagging模型,而ET是使用所有的训练样本得到每棵决策树,也就是每棵决策树应用的是相同的全部训练样本
            关于Bagging和Boosting的差别,可以参考 https://www.cnblogs.com/earendil/p/8872001.html
        2.随机森林是在一个随机子集内得到最佳分叉属性,而ET是完全随机的得到分叉值,从而实现对决策树进行分叉的
        
 Gradient Boosting - 迭代的时候选择梯度下降的方向来保证最后的结果最好
                            损失函数用来描述模型的'靠谱'程度,假设模型没有过拟合,损失函数越大,模型的错误率越高
                            如果我们的模型能够让损失函数持续的下降,最好的方式就是让损失函数在其梯度方向下降
                            
                            GradientBoostingRegressor()
                                    loss - 选择损失函数，默认值为ls(least squres),即最小二乘法,对函数拟合
                                            1.lad - 绝对损失
                                            2.huber - Huber损失
                                            3.quantile - 分位数损失
                                            4.ls - 均方差损失(默认)
                                    learning_rate - 学习率
                                    n_estimators - 弱学习器的数目,默认值100
                                    max_depth - 每一个学习器的最大深度,限制回归树的节点数目,默认为3
                                    min_samples_split - 可以划分为内部节点的最小样本数,默认为2
                                    min_samples_leaf - 叶节点所需的最小样本数,默认为1
                                    alpha - 当我们使用Huber损失和分位数损失'quantile'时,需要指定分位数的值,只有regressor有
                                    
                            GradientBoostingClassifier() - 参数绝大多数和Regressor相同,不同的是loss函数
                                            1.deviance - 对数似然损失函数(默认)
                                            2.exponential - 指数损失函数       
参考网址: https://www.cnblogs.com/pinard/p/6143927.html
'''
clfs = [LogisticRegression(solver='lbfgs'),
        RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
        ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
        ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='entropy'),
        GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=5)]


# ## 切分一部分数据作为测试集
X, X_predict, y, y_predict = train_test_split(data, target, test_size=0.3, random_state=2020)

dataset_blend_train = np.zeros((X.shape[0], len(clfs)))  # 全零数组,行取训练集的个数,列取模型个数
dataset_blend_test = np.zeros((X_predict.shape[0], len(clfs)))    # 全零数组,行取测试集的个数,列取模型个数

# 5折Stacking - 即每次Stacking训练都会在第一层基学习器进行5折交叉验证,再进入第二层学习器训练

n_splits = 5
skf = StratifiedKFold(n_splits)     # # 分层交叉验证,每一折中都保持着原始数据中各个类别的比例关系(测试集和训练集分离)
skf = skf.split(X, y)     # 把特征和标签分离

'''
enumerate() - 用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在for循环当中
'''
for j, clf in enumerate(clfs):
    # 依次训练各个单模型
    dataset_blend_test_j = np.zeros((X_predict.shape[0], len(clfs)))    # 30行5列的全0数组
    # 五折交叉训练,使用第i个部分作为预测集,剩余部分为验证集,获得的预测值成为第i部分的新特征
    for i, (train, test) in enumerate(skf):
        X_train, y_train, X_test, y_test = X[train], y[train], X[test], y[test]
        clf.fit(X_train, y_train)
        # 将对测试集的概率预测第二列(也就是结果为1)的概率装进y_submission中
        y_submission = clf.predict_proba(X_test)[:, 1]
        dataset_blend_train[test, j] = y_submission     # 把预测验证集(比如第一折)的结果依次对应装进dataset_blend_train中
        '''
        predict_proba() - 返回的是一个n行k列的数组
                            第i行第j列上的数值是模型预测第i个预测样本为某个标签的概率,并且每一行的概率和为1
        '''
        '''
        因为我们采取到的数据集的标签只有0或1,所以predict_proba返回的概率只有两个
                    如果左边的概率大于0.5,那么预测值为0
                    如果右边的概率大于0.5,那么预测值为1
        '''
        # # 将对测试集的概率预测的第二列(也就是结果为1)的概率装进dataset_blend_test_j中
        dataset_blend_test_j[:, i] = clf.predict_proba(X_predict)[:, 1]
    # 对于测试集,直接用这5个模型的预测值均值作为新的特征
    dataset_blend_test[:, j] = dataset_blend_test_j.mean(1)     # mean(1) - 求每行数的平均值(五折预测测试集的平均值)
    print('val auc Score: %f' % roc_auc_score(y_predict, dataset_blend_test[:, j]))

clf = LogisticRegression(solver='lbfgs')    # 次级学习器再次训练
clf.fit(dataset_blend_train, y)     # 把第一层得到训练集的预测结果作为新特征,把训练集的真实标签作为标签,进行第二层训练
y_submission = clf.predict_proba(dataset_blend_test)[:, 1]  # 把第一层预测测试集的结果作为新特征,预测测试集的标签
'''
ROC曲线和AUC - 用来评价一个二值分类器(binary classifier)的优劣,用于衡量'二分类问题'机器学习算法性能(泛化能力)
AUC - ROC曲线下的面积
      AUC的取值范围在0.5和1之间
      使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好
      而作为一个数值,对应AUC更大的分类器效果更好
'''
print('Val auc Score of Stacking: %f' % (roc_auc_score(y_predict, y_submission)))


val auc Score: 1.000000
val auc Score: 0.500000
val auc Score: 0.500000
val auc Score: 0.500000
val auc Score: 0.500000
Val auc Score of Stacking: 1.000000

# Blending - 和Stacking类似,不同点在于:

'''
1.Stacking - 把第一层得到训练集的预测结果作为新特征,把训练集的真实标签作为标签,进行第二层训练
2.Blending - 把第一层得到训练集中的30%的验证集的结果作为新特征继续训练,把训练集的真实标签作为标签,进行第二层训练

Blending优点 - 比stacking简单,因为不用进行k次的交叉验证来获得stacker feature
                避开了一个信息泄露问题：generlizers和stacker使用了不一样的数据集
Blending缺点- 使用了很少的数据,可能会过拟合,没有stacking使用多次的交叉验证来的稳健
'''
data_0 = iris.data
data = data_0[:100, :]
target_0 = iris.target
target = target_0[:100]

clfs = [LogisticRegression(solver='lbfgs'),
        RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
        RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='entropy'),
        ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
        GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=5)]

# 划分训练集和测试集
X, X_predict, y, y_predict = train_test_split(data, target, test_size=0.3, random_state=2020)

# 把训练数据分成d1(子训练集),d2(验证集)两部分 - 对半分
X_d1, X_d2, y_d1, y_d2 = train_test_split(X, y, test_size=0.5, random_state=2020)
dataset_d1 = np.zeros((X_d2.shape[0], len(clfs)))   # 35行5列的全0数组
dataset_d2 = np.zeros((X_predict.shape[0], len(clfs)))      # 30行5列的全0数组

for j, clf in enumerate(clfs):
    # 用子训练集依次训练各个模型
    clf.fit(X_d1, y_d1)
    # 返回模型对验证集的预测值为1的概率
    y_submission = clf.predict_proba(X_d2)[:, 1]
    # 结果装进dataset_d1中 - 表示用子训练集训练的模型预测验证集标签的结果 - 就是上文说的30%的数据
    dataset_d1[:, j] = y_submission
    # 建立第二层模型的特征 - 用第一层模型预测测试集的结果作为新的特征
    dataset_d2[:, j] = clf.predict_proba(X_predict)[:, 1]
    # 看一下预测的预测集标签和真实的预测集标签的roc_auc_score
    print('val auc Score: %f' % roc_auc_score(y_predict, dataset_d2[:, j]))

# 用第二层模型训练特征
clf = GradientBoostingClassifier(learning_rate=0.02, subsample=0.5, max_depth=6, n_estimators=30)
clf.fit(dataset_d1, y_d2)   # 用验证集的第一层模型预测结果作为特征,用验证集的真实标签作为标签,再次训练
y_submission = clf.predict_proba(dataset_d2)[:, 1]  # 用第一层模型预测测试集的结果作为特征,用第二层模型预测训练集返回1的概率
print('Val auc Score of Blending: %f' % (roc_auc_score(y_predict, y_submission)))



val auc Score: 1.000000
val auc Score: 1.000000
val auc Score: 1.000000
val auc Score: 1.000000
val auc Score: 1.000000
Val auc Score of Blending: 1.000000

# 利用mlxtend进行分类的Stacking融合

iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()

'''
StackingClassifier() - 快速Stacking融合的方法

参数详解:
classifiers - 一级分类器列表
meta_classifier - 二级分类器(元分类器)
use_probas - 如果为True,则基于预测的概率而不是类标签来训练元分类器,默认为False
average_probas - 如果为真,将概率平均为元特征,默认为False
verbose - 是否输出到日志
'''
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
                          meta_classifier=lr)
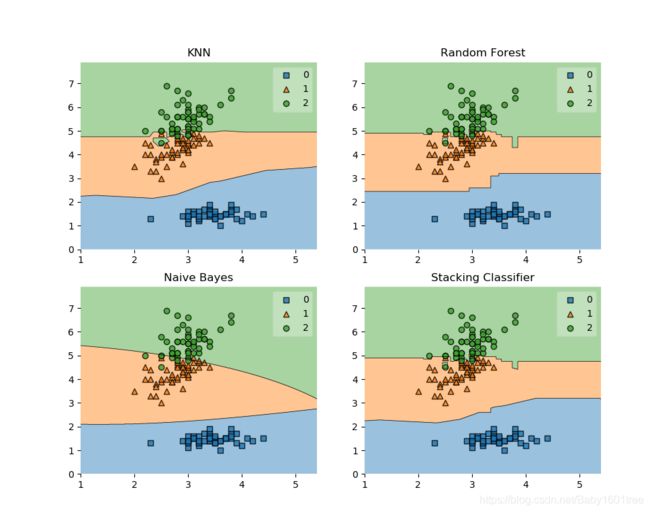
label = ['KNN', 'Random Forest', 'Naive Bayes', 'Stacking Classifier']
clf_list = [clf1, clf2, clf3, sclf]

fig = plt.figure(figsize=(10, 8))
gs = gridspec.GridSpec(2, 2)    # 网格布局,每行2个,每列2个
grid = itertools.product([0, 1], repeat=2)  # 求多个可迭代对象的笛卡尔积,其实就是更加灵活调整网格的大小

clf_cv_mean = []    # 存放每个模型的准确率的均值
clf_cv_std = []     # 存放每个模型的准确率的标准差
for clf, label, grd in zip(clf_list, label, grid):

    scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')   # 3折交叉验证,评分标准为模型准确率
    print('Accuracy: %.2f (+/- %.2f) [%s]' % (scores.mean(), scores.std(), label))
    clf_cv_mean.append(scores.mean())
    clf_cv_std.append(scores.std())

    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf)
    plt.title(label)
plt.show()



Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [Stacking Classifier]

可以看出,融合后的曲线更加优秀

# 一些其它方法

'''
将特征放进模型中预测,并将预测结果变换并作为新的特征加入原有特征中,再经过模型预测结果(Stacking变化)
可以反复预测多次将结果加入最后的特征中
'''


def ensemble_add_feature(train, test, target, clfs):
    # n_folds = 5
    # skf = list(StratifiedKFold(y, n_folds=n_folds))
    train_ = np.zeros((train.shape[0], len(clfs * 2)))
    test_ = np.zeros((test.shape[0], len(clfs * 2)))
    for j, clf in enumerate(clfs):
        # 依次训练单个模型
        print(j, clf)
        # 使用第1部分作为预测,第2部分来训练模型(第1部分预测的输出作为第2部分的新特征)
        # X_train, y_train, X_test, y_test = X[train], y[train]
        clf.fit(train, target)  # 训练模型
        y_train = clf.predict(train)    # 模型在训练集中的预测值
        y_test = clf.predict(test)      # 模型在测试集中的预测值

        # 生成新特征
        '''
        j 从0开始递增,构建新的特征集,特征为训练集和测试集各自的预测值的平方
        '''
        train_[:, j*2] = y_train ** 2
        test_[:, j*2] = y_test ** 2
        train_[:, j+1] = np.exp(y_train)    # np.exp(a) - 返回e的a次方
        test_[:, j+1] = np.exp(y_test)
        print('Method:', j)
    train_ = pd.DataFrame(train_)
    test_ = pd.DataFrame(test_)
    return train_, test_


clf = LogisticRegression()  # 次级模型
data_0 = iris.data
data = data_0[:100, :]
target_0 = iris.target
target = target_0[:100]

x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.3)
x_train = pd.DataFrame(x_train)     # 转换成DataFrame格式,方便后续构造新特征
x_test = pd.DataFrame(x_test)

# 给出模型融合中使用到的各个单模型
clfs = [LogisticRegression(),
        RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
        ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
        ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='entropy'),
        GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=5)]
# 新特征的构造 - 用上面的各个单模型预测训练集和测试集的结果,作为新特征
New_train, New_test = ensemble_add_feature(x_train, x_test, y_train, clfs)
clf.fit(New_train, y_train)     # 用训练集的新特征和训练集的真实标签训练数据
y_emb = clf.predict_proba(New_test)[:, 1]   # 用训练好的模型得到新的测试集特征返回1的概率
print('Val auc Score of Stacking: %f' % (roc_auc_score(y_test, y_emb)))



Method: 4
Val auc Score of Stacking: 1.000000

关于模型融合的理论和方法具体可以参考：https://github.com/datawhalechina/team-learning-data-mining/blob/master/FinancialRiskControl/Task5%20%E6%A8%A1%E5%9E%8B%E8%9E%8D%E5%90%88.md

这边文章由于时间关系，只提供了一个大致的思路，具体调参以及之后的融合可以参照task4和上文提供的链接尝试。

导入三方模块

import pandas as pd
import numpy as np
import datetime
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import KFold, train_test_split, StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import xgboost as xgb
from sklearn.metrics import roc_auc_score
import warnings
warnings.filterwarnings('ignore')
pd.options.display.max_columns = None
pd.set_option('display.float_format', lambda x: '%.2f' % x)

做模型融合之前，我要做两件事情：特征筛选和模型选择

'''
特征筛选：随机森林或SFS挑选最优特征
模型选择：xgboost, lightgbm, logistic 加权融合。或者再加线性回归模型嵌套一个弱分类器学习预测
'''

不同模型的数据准备注意点

'''
使用xgboost要注意的点：
    1.在Xgb中需要将离散特征one-hot编码再和连续特征一起输入训练，这样做是为了达到在cart树中处理离散特征的方式一致
    2.无需处理缺失值，在Xgb中处理稀疏数据时，没有值的特征是走默认的分支，所以在Xgb中缺省值也是走默认分支
lightgbm:
    1.由于使用直方图算法，LightGBM直接支持类别特征，对类别特征不必进行独热编码处理（与xgboost不同）
    2.也可以直接处理缺失值
logistic:
    1.数据要进行缺失值和异常值的处理
    2.类别数据要做one-hot编码
    3.对于某些方差大的特征，建议做归一化处理以增强模型稳定性
'''

读取、压缩数据

train = pd.read_csv(r'D:\Users\Felixteng\Documents\Pycharm Files\loanDefaultForecast\data\train.csv')
testA = pd.read_csv(r'D:\Users\Felixteng\Documents\Pycharm Files\loanDefaultForecast\data\testA.csv')


def reduce_mem_usage(df):
    '''
    遍历DataFrame的所有列并修改它们的数据类型以减少内存使用
    :param df: 需要处理的数据集
    :return:
    '''
    start_mem = df.memory_usage().sum() / 1024 ** 2  # 记录原数据的内存大小
    print('Memory usage of dataframe is {:.2f} MB'.format(start_mem))
    for col in df.columns:
        col_type = df[col].dtypes
        if col_type != object:  # 这里只过滤了object格式，如果代码中还包含其他类型，要一并过滤
            c_min = df[col].min()
            c_max = df[col].max()
            if str(col_type)[:3] == 'int':  # 如果是int类型的话,不管是int64还是int32,都加入判断
                # 依次尝试转化成in8,in16,in32,in64类型,如果数据大小没溢出,那么转化
                if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
                    df[col] = df[col].astype(np.int8)
                elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
                    df[col] = df[col].astype(np.int16)
                elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
                    df[col] = df[col].astype(np.int32)
                elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
                    df[col] = df[col].astype(np.int64)
            else:  # 不是整形的话,那就是浮点型
                if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
                    df[col] = df[col].astype(np.float16)
                elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
                    df[col] = df[col].astype(np.float32)
                else:
                    df[col] = df[col].astype(np.float64)
        else:  # 如果不是数值型的话,转化成category类型
            df[col] = df[col].astype('category')

    end_mem = df.memory_usage().sum() / 1024 ** 2    # 看一下转化后的数据的内存大小
    print('Memory usage after optimization is {:.2f} MB'.format(end_mem))
    print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem) / start_mem))  # 看一下压缩比例
    return df


train = reduce_mem_usage(train)
testA = reduce_mem_usage(testA)
del testA['n2.2']
del testA['n2.3']

为了方便起见，把训练集和测试集合并处理

data = pd.concat([train, testA], axis=0, ignore_index=True)

lgb

字段 employmentLength - 10年以上算10年，1年一下算0年；然后转化成数值

data['employmentLength'].replace(to_replace='10+ years', value='10 years', inplace=True)
data['employmentLength'].replace(to_replace='< 1 year', value='0 year', inplace=True)


def employmentLength_to_int(s):
    if pd.isnull(s):
        return s
    else:
        return np.int8(s.split()[0])


data['employmentLength'] = data['employmentLength'].apply(employmentLength_to_int)

字段 earliesCreditLine - 分别提取年份和月份做拼接

data['earliesCreditLine_year'] = data['earliesCreditLine'].apply(lambda x: x[-4:])
data['earliesCreditLine_month'] = data['earliesCreditLine'].apply(lambda x: x[0:3])


def month_re(x):
    if x == 'Jan':
        return '01'
    elif x == 'Feb':
        return '02'
    elif x == 'Mar':
        return '03'
    elif x == 'Apr':
        return '04'
    elif x == 'May':
        return '05'
    elif x == 'Jun':
        return '06'
    elif x == 'Jul':
        return '07'
    elif x == 'Aug':
        return '08'
    elif x == 'Sep':
        return '09'
    elif x == 'Oct':
        return '10'
    elif x == 'Nov':
        return '11'
    else:
        return '12'


data['earliesCreditLine_month'] = data['earliesCreditLine_month'].apply(lambda x: month_re(x))
data['earliesCreditLine_date'] = data['earliesCreditLine_year'] + data['earliesCreditLine_month']
data['earliesCreditLine_date'] = data['earliesCreditLine_date'].astype('int')
del data['earliesCreditLine']
del data['earliesCreditLine_year']
del data['earliesCreditLine_month']

字段 issueDate - 从2017年6月1日开始；数据按照此节点统计天数

data['issueDate'] = pd.to_datetime(data['issueDate'], format='%Y-%m-%d')
startdate = datetime.datetime.strptime('2007-06-01', '%Y-%m-%d')
data['issueDateDt'] = data['issueDate'].apply(lambda x: x - startdate).dt.days
del data['issueDate']

看一下特征的类别分布情况

cate_features = ['grade', 'subGrade', 'employmentTitle', 'homeOwnership', 'verificationStatus', 'purpose',
                 'postCode', 'regionCode', 'applicationType', 'initialListStatus', 'title', 'policyCode']
for cate in cate_features:
    print(cate, '类型数', data[cate].nunique())
'''
不适合做one-hot编码的是
    employmentTitle 类型数 298101
    postCode 类型数 935
    title 类型数 6712
    regionCode 类型数 51 - 大于50的先不处理了，维度还是比较高的
    policyCode 类型数 1 - 无分析价值，可直接删除
'''
del data['policyCode']

对于高维类别特征，进行转换，取他们同类型的数量值和排名值

for f in ['employmentTitle', 'postCode', 'regionCode', 'title']:
    data[f + '_counts'] = data.groupby([f])['id'].transform('count')
    data[f + '_rank'] = data.groupby([f])['id'].rank(ascending=False).astype(int)
    del data[f]

features = [f for f in data.columns if f not in ['id', 'isDefault']]
train_lgb = data[data.isDefault.notnull()].reset_index(drop=True)
testA_lgb = data[data.isDefault.isnull()].reset_index(drop=True)

保存数据待用

train_lgb.to_csv('./data/train_data_for_lgb.csv', index=0)
testA_lgb.to_csv('./data/testA_data_for_lgb.csv', index=0)

xgb - 主要one-hot类别特征

对于维度大于1且不会形成高维稀疏矩阵的特征，进行one-hot编码

data_xgb = data
data_xgb = pd.get_dummies(data_xgb, columns=['grade', 'subGrade', 'homeOwnership', 'verificationStatus',
                                             'purpose', 'applicationType', 'initialListStatus'], drop_first=True)
train_xgb = data_xgb[data_xgb.isDefault.notnull()].reset_index(drop=True)
testA_xgb = data_xgb[data_xgb.isDefault.isnull()].reset_index(drop=True)

保存数据待用

train_xgb.to_csv('./data/train_data_for_xgb.csv')
testA_xgb.to_csv('./data/testA_data_for_xgb.csv')

logistic - 主要处理特征的缺失值、异常值、连续特征的归一化及数据分桶

data_logistic = data_xgb

缺失值的处理

我没有选择删除数据（每条数据都是宝贵的），能补就补

看看缺失数据

missing = data_logistic.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(ascending=False, inplace=True)
missing.plot.bar()

可以发现，有缺失值的特征不多，就22个；其中缺失率比较高的有16个，基本都是匿名特征且缺失率均在10%以下

看下匿名特征的分布情况，判断一下是离散特征还是连续特征

n_features = ['n0', 'n1', 'n2', 'n2.1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n9', 'n10', 'n11', 'n12', 'n13', 'n14']
for n in n_features:
    print(n, '类型数', data_logistic[n].nunique())

data_logistic[['employmentLength', 'n0', 'n1', 'n2', 'n2.1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n9',
                'n10', 'n11']].head(50)
data_logistic[['employmentLength', 'n0', 'n1', 'n2', 'n2.1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n9', 'n10', 'n11']].info()

去重以后值不多，看着像离散型特征

我先统一将这些匿名特征的缺失值单独分一类

missing_features_part = ['n0', 'n1', 'n2', 'n2.1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n9', 'n10', 'n11', 'n12', 'n13',
                         'n14']
for missfea in missing_features_part:
    data_logistic.fillna({
     missfea: -99}, inplace=True)
    data_logistic[missfea] = data_logistic[missfea].astype('category')
    print('{} 处理完成'.format(missfea))

剩下有缺失数据的特征如下

'''
employmentLength           58541
dti                          300
pubRecBankruptcies           521
revolUtil                    658
employmentTitle_counts         1
postCode_counts                1
title_counts                   1
'''

employmentLength是就业年限，和逾期应该不是强关联的特征，另外几个特征缺失很少，使用出现最多的分类变量来代替缺失值

fea_miss = ['employmentLength', 'revolUtil', 'pubRecBankruptcies', 'dti', 'employmentTitle_counts',
            'postCode_counts', 'title_counts']

employmentLength

data_logistic.groupby('employmentLength')['isDefault'].count().sort_values(ascending=False)
'''10'''
data_logistic.fillna({
     'employmentLength': 10}, inplace=True)

revolUtil

data_logistic.groupby('revolUtil')['isDefault'].count().sort_values(ascending=False)
'''0.00'''
data_logistic.fillna({
     'revolUtil': 0.00}, inplace=True)

pubRecBankruptcies

data_logistic.groupby('pubRecBankruptcies')['isDefault'].count().sort_values(ascending=False)
'''0.00'''
data_logistic.fillna({
     'pubRecBankruptcies': 0.00}, inplace=True)

dti

data_logistic.groupby('dti')['isDefault'].count().sort_values(ascending=False)
'''16.80'''
data_logistic.fillna({
     'dti': 16.80}, inplace=True)

employmentTitle_counts

data_logistic.groupby('employmentTitle_counts')['isDefault'].count().sort_values(ascending=False)
'''1.00'''
data_logistic.fillna({
     'employmentTitle_counts': 1.00}, inplace=True)

postCode_counts

data_logistic.groupby('postCode_counts')['isDefault'].count().sort_values(ascending=False)
'''11092.00'''
data_logistic.fillna({
     'postCode_counts': 11092.00}, inplace=True)

title_counts

data_logistic.groupby('title_counts')['isDefault'].count().sort_values(ascending=False)
'''491400.00'''
data_logistic.fillna({
     'title_counts': 491400.00}, inplace=True)

随机森林筛选重要特征

num_features = list(data_logistic.select_dtypes(exclude=['category']).columns)
'''数值型特征'''
cate_features = list(data_logistic.select_dtypes(include=['category']).columns)
'''类别型特征'''

for fea in cate_features:
    data_logistic[fea] = data_logistic[fea].astype('int')

# ## 分离训练集和测试集
train_logistic_forest = data_logistic[data_logistic.isDefault.notnull()].reset_index(drop=True)
features = [f for f in train_logistic_forest.columns if f not in ['id', 'isDefault']]
label = ['isDefault']
X_train_logistic_forest = train_logistic_forest[features]
y_train_logistic_forest = train_logistic_forest[label]
# ## 使用随机森林训练
clf_forest = RandomForestClassifier()
clf_forest.fit(X_train_logistic_forest, y_train_logistic_forest)

得到特征重要性

forest_importances = list(clf_forest.feature_importances_)
feature_importances = [(feature, round(importance, 2)) for feature, importance in zip(
    features, forest_importances)]

# ## 重要性排序
feature_importances = sorted(feature_importances, key=lambda x: x[1], reverse=True)
print(feature_importances)

重要性为0的特征就不保留了，不然内存占用太大了

important_features = ['interestRate', 'dti', 'revolBal', 'revolUtil', 'earliesCreditLine_date',
                      'title_rank', 'loanAmnt', 'installment', 'annualIncome', 'totalAcc',
                      'issueDateDt', 'employmentTitle_rank', 'postCode_counts', 'postCode_rank',
                      'regionCode_rank', 'term', 'employmentLength', 'ficoRangeLow', 'ficoRangeHigh',
                      'openAcc', 'n1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n10', 'n14',
                      'employmentTitle_counts', 'regionCode_counts', 'delinquency_2years', 'pubRec',
                      'n0', 'n2', 'n2.1', 'n9', 'title_counts', 'grade_E', 'homeOwnership_1']
'''
[('interestRate', 0.05), ('dti', 0.04), ('revolBal', 0.04), ('revolUtil', 0.04), 
('earliesCreditLine_date', 0.04), ('title_rank', 0.04), ('loanAmnt', 0.03), ('installment', 0.03), 
('annualIncome', 0.03), ('totalAcc', 0.03), ('issueDateDt', 0.03), ('employmentTitle_rank', 0.03), 
('postCode_counts', 0.03), ('postCode_rank', 0.03), ('regionCode_rank', 0.03), ('term', 0.02), 
('employmentLength', 0.02), ('ficoRangeLow', 0.02), ('ficoRangeHigh', 0.02), ('openAcc', 0.02), 
('n1', 0.02), ('n4', 0.02), ('n5', 0.02), ('n6', 0.02), ('n7', 0.02), ('n8', 0.02), ('n10', 0.02), 
('n14', 0.02), ('employmentTitle_counts', 0.02), ('regionCode_counts', 0.02), 
('delinquency_2years', 0.01), ('pubRec', 0.01), ('n0', 0.01), ('n2', 0.01), ('n2.1', 0.01), 
('n9', 0.01), ('title_counts', 0.01), ('grade_E', 0.01), ('homeOwnership_1', 0.01), 
'''

columns = ['interestRate', 'dti', 'revolBal', 'revolUtil', 'earliesCreditLine_date',
           'title_rank', 'loanAmnt', 'installment', 'annualIncome', 'totalAcc',
           'issueDateDt', 'employmentTitle_rank', 'postCode_counts', 'postCode_rank',
           'regionCode_rank', 'term', 'employmentLength', 'ficoRangeLow', 'ficoRangeHigh',
           'openAcc', 'n1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n10', 'n14', 'employmentTitle_counts',
           'regionCode_counts', 'delinquency_2years', 'pubRec', 'n0', 'n2', 'n2.1', 'n9',
           'title_counts', 'grade_E', 'homeOwnership_1', 'isDefault']

# ## 将重要性为零的特征都不保留了
data_logistic = data_logistic[columns]

异常数据处理

对于异常值，这里不做处理，将数值型特征做归一化处理，降低异常值的干扰。归一化前先去对数
为什么要取对数 - 数据集中有负数就不能取对数了 - 实践中,取对数的一般是水平量,而不是比例数据
1.缩小数据的绝对数值,方便计算
2.取对数后,可以将乘法计算转换称加法计算
3.对数值小的部分差异的敏感程度比数值大的部分的差异敏感程度更高
4.取对数之后不会改变数据的性质和相关关系,但压缩了变量的尺度
5.所得到的数据易消除异方差问题

def min_max_scaler(data, fea):
    data[fea] = np.log(data[fea] + 2)   # 数据中有-1
    data[fea] = ((data[fea] - np.min(data[fea])) / (np.max(data[fea]) - np.min(data[fea]))) # 归一化


min_max_columns = list(data_logistic.select_dtypes(exclude=['uint8']).columns)
min_max_columns.remove('isDefault')

for col in min_max_columns:
    min_max_scaler(data_logistic, col)


data_logistic.info()

两个数据集分开

train_logistic = data_logistic[data_logistic.isDefault.notnull()].reset_index(drop=True)
testA_logistic = data_logistic[data_logistic.isDefault.isnull()].reset_index(drop=True)

train_logistic.to_csv('./data/train_data_for_logistic.csv', index=0)
testA_logistic.to_csv('./data/testA_data_for_logistic.csv', index=0)

模型训练

logistic

数据准备

train_logistic = pd.read_csv('./data/train_data_for_logistic.csv')
testA_logistic = pd.read_csv('./data/testA_data_for_logistic.csv')
missing_fea = ['n1', 'n4', 'n5', 'n6', 'n7', 'n8', 'n10', 'n14', 'n0', 'n2', 'n2.1', 'n9']
train_logistic.info()
train_logistic[missing_fea] = train_logistic[missing_fea].fillna(train_logistic[missing_fea].median())
testA_logistic[missing_fea] = testA_logistic[missing_fea].fillna(testA_logistic[missing_fea].median())

划分训练集的特征和标签

features = [f for f in train_logistic.columns if f not in ['isDefault']]
label = ['isDefault']
X_train_logistic = train_logistic[features]
y_train_logistic = train_logistic[label]

将训练集分为5份，4份作为训练集，1份作为验证集

X_train_logistic_split, X_val_logistic, y_train_logistic_split, y_val_logistic = train_test_split(
    X_train_logistic, y_train_logistic, test_size=0.2)
lr = LogisticRegression()
lr = lr.fit(X_train_logistic_split, y_train_logistic_split)
y_val_logistic_pre = lr.predict(X_val_logistic)
fpr, tpr, threshold = metrics.roc_curve(y_val_logistic, y_val_logistic_pre)
roc_auc = metrics.auc(fpr, tpr)
print('未调参前逻辑回归在验证集上的AUC： {}'.format(roc_auc))
'''
未调参前逻辑回归在验证集上的AUC： 0.531000169605175

欠拟合
'''

找出相关性高的特征

print(lr.coef_)
m = {
     }
col_name = list(X_train_logistic_split.columns)
for i in range(len(col_name)):
    # 若没有key,加入key
    m.setdefault(col_name[i], 0)
    # 这里取绝对值，主要看特征的相关性
    m[col_name[i]] = abs(lr.coef_[0][i])

sorted(m.items(), key=lambda x: x[1], reverse=True)

大家这里可以尝试用相关性高的特征加以处理或特征构造，重新训练模型。我这里也没有调参，可以通过调参提高结果分数

xgboost

数据准备

train_xgb = pd.read_csv('./data/train_data_for_xgb.csv')
testA_xgb = pd.read_csv('./data/testA_data_for_xgb.csv')

features_xgb = [f for f in train_xgb.columns if f not in ['isDefault']]
X_train_xgb = train_xgb[features_xgb]
y_train_xgb = train_xgb['isDefault']

## xgb - 梯度提升决策树

‘’’
XGBRegressor - 梯度提升回归树,也叫梯度提升机

            采用连续的方式构造树,每棵树都试图纠正前一棵树的错误
            与随机森林不同,梯度提升回归树没有使用随机化,而是用到了强预剪枝
            从而使得梯度提升树往往深度很小,这样模型占用的内存少,预测的速度也快

            gamma - 定了节点分裂所需的最小损失函数下降值,这个参数的值越大,算法越保守
            subsample - 这个参数控制对于每棵树随机采样的比例,减小这个参数的值,算法会更加保守,避免过拟合
            colsample_bytree - 用来控制每棵随机采样的列数的占比
            learning_rate - 学习速率,用于控制树的权重,xgb模型在进行完每一轮迭代之后,会将叶子节点的分数乘上该系数,
                            以便于削弱各棵树的影响,避免过拟合

‘’’

def build_model_xgb(x_train, y_train):
    model = xgb.XGBRegressor(n_estimators=120, learning_rate=0.08, gamma=0,
                             subsample=0.8, colsample_bytree=0.9, max_depth=5)
    model.fit(x_train, y_train)
    return model


# xgb五折交叉验证
xgr = xgb.XGBClassifier(n_estimators=120, learning_rate=0.1, subsample=0.8, colsample_bytree=0.9, max_depth=7)

scores_train = []   # 每次模型训练训练集中子训练集的得分
scores = []         # 每次模型训练训练集中验证集的得分

sk = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)  # shuffle判断是否在每次抽样时对样本进行清洗
for train_ind, val_ind in sk.split(X_train_xgb, y_train_xgb):
    train_x = X_train_xgb.iloc[train_ind].values
    train_y = y_train_xgb.iloc[train_ind]
    val_x = X_train_xgb.iloc[val_ind].values
    val_y = y_train_xgb.iloc[val_ind]

    xgr.fit(train_x, train_y)
    pred_train_xgb = xgr.predict(train_x)   # 子训练集的预测值
    pre_xgb = xgr.predict(val_x)            # 验证集的预测值

    scores_train.append(roc_auc_score(train_y, pred_train_xgb))
    scores.append(roc_auc_score(val_y, pre_xgb))                    # 统计验证集的mae

print('Train mae:', np.mean(scores_train))  # 统计mae均值
print('Val mae:', np.mean(scores))
'''
Train mae: 0.5548858423493594
Val mae: 0.5458927786959327
'''

结果也不是很好，同样可以通过特征重新筛选和调参来提高

总结

至于lgb部分，可以参考Task4的代码，思路就是使用lgb,xgb,lr同时找到合适的特征并加以调参。训练完后三个模型可以使用文初提到的链接使用stacking、blending、加权融合或者投票（硬投票、软投票等方法）尝试模型融合。

在task5之后，我自己还会做一个task6，尝试完整的完成预测，再到线上提交加以迭代。