姓名:崔升 学号:14020120005
转载自:http://www.cnblogs.com/en-heng/p/5173704.html
【嵌牛导读】:
AdaBoost是一种通过多个基分类器来完成学习任务的一种算法
【嵌牛鼻子】:经典大数据算法之AdaBoost算法的简单介绍
【嵌牛提问】:PageRank是一种怎么的算法,其如何通过多个分类的任务来完成学习系统呢?
【嵌牛正文】:
1. 集成学习
集成学习(ensemble learning)通过组合多个基分类器(base classifier)来完成学习任务,颇有点“三个臭皮匠顶个诸葛亮”的意味。基分类器一般采用的是弱可学习(weakly learnable)分类器,通过集成学习,组合成一个强可学习(strongly learnable)分类器。所谓弱可学习,是指学习的正确率仅略优于随机猜测的多项式学习算法;强可学习指正确率较高的多项式学习算法。集成学习的泛化能力一般比单一的基分类器要好,这是因为大部分基分类器都分类错误的概率远低于单一基分类器的。
偏差与方差
“偏差-方差分解”(bias variance decomposition)是用来解释机器学习算法的泛化能力的一种重要工具。对于同一个算法,在不同训练集上学得结果可能不同。对于训练集D={(x1,y1),(x2,y2),⋯,(xN,yN)}D={(x1,y1),(x2,y2),⋯,(xN,yN)},由于噪音,样本xx的真实类别为yDyD(在训练集中的类别为yy),则噪声为
ξ2=ED[(yd−y)2]ξ2=ED[(yd−y)2]
学习算法的期望预测为
f¯(x)=ED[f(x;D)]f¯(x)=ED[f(x;D)]
使用样本数相同的不同训练集所产生的方法
var(x)=ED[(f(x;D)−f¯(x))2]var(x)=ED[(f(x;D)−f¯(x))2]
期望输入与真实类别的差别称为bias,则
bias2(x)=(f¯(x)−y)2bias2(x)=(f¯(x)−y)2
为便于讨论,假定噪声的期望为0,即ED[yd−y]=0ED[yd−y]=0,通过多项式展开,可对算法的期望泛化误差进行分解(详细的推导参看[2]):
ED[(f(x;D)−yD)2]=ED[(f(x;D)−f¯(x)+f¯(x)−yD)2]=ED[(f(x;D)−f¯(x))2]+(f¯(x)−y)2+ED[(yD−y)2]=bias2(x)+var(x)+ξ2ED[(f(x;D)−yD)2]=ED[(f(x;D)−f¯(x)+f¯(x)−yD)2]=ED[(f(x;D)−f¯(x))2]+(f¯(x)−y)2+ED[(yD−y)2]=bias2(x)+var(x)+ξ2
也就是说,误差可以分解为3个部分:bias、variance、noise。bias度量了算法本身的拟合能力,刻画模型的准确性;variance度量了数据扰动所造成的影响,刻画模型的稳定性。为了取得较好的泛化能力,则需要充分拟合数据(bias小),并受数据扰动的影响小(variance小)。但是,bias与variance往往是不可兼得的:
当训练不足时,拟合能力不够强,数据扰动不足以产生较大的影响,此时bias主导了泛化错误率;
随着训练加深时,拟合能力随之加强,数据扰动渐渐被学习到,variance主导了泛化错误率。
Bagging与Boosting
集成学习需要解决两个问题:
如何调整输入训练数据的概率分布及权值;
如何训练与组合基分类器。
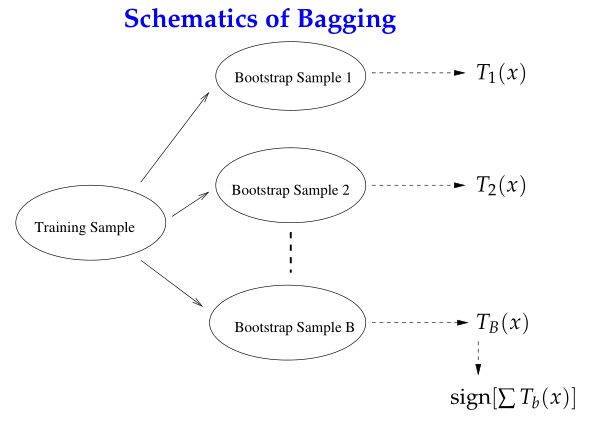
从上述问题的角度出发,集成学习分为两类流派:Bagging与Boosting。Bagging(BootstrapAggregating)对训练数据擦用自助采样(boostrap sampling),即有放回地采样数据;每一次的采样数据集训练出一个基分类器,经过MM次采样得到MM个基分类器,然后根据最大表决(majority vote)原则组合基分类器的分类结果。
Boosting的思路则是采用重赋权(re-weighting)法迭代地训练基分类器,即对每一轮的训练数据样本赋予一个权重,并且每一轮样本的权值分布依赖上一轮的分类结果;基分类器之间采用序列式的线性加权方式进行组合。
从“偏差-方差分解”的角度看,Bagging关注于降低variance,而Boosting则是降低bias;Boosting的基分类器是强相关的,并不能显著降低variance。Bagging与Boosting有分属于自己流派的两大杀器:Random Forests(RF)和Gradient Boosting Decision Tree(GBDT)。本文所要讲的AdaBoost属于Boosting流派。
2. AdaBoost算法
AdaBoost是由Freund与Schapire [1] 提出来解决二分类问题y∈{0,1}y∈{0,1},其定义损失函数为指数损失函数:
L(y,f(x))=exp(−yf(x))(1)(1)L(y,f(x))=exp(−yf(x))
根据加型模型(additive model),第mm轮的分类函数
fm(x)=fm−1(x)+αmGm(x)fm(x)=fm−1(x)+αmGm(x)
其中,αmαm为基分类器Gm(x)Gm(x)的组合系数。AdaBoost采用前向分布(forward stagewise)这种贪心算法最小化损失函数(1)(1),求解子模型的αmαm
αm=12log1−ememαm=12log1−emem
其中,emem为Gm(x)Gm(x)的分类误差率。第m+1m+1轮的训练数据集权值分布Dm+1=(wm+1,1,⋯,wm+1,i,⋯,wm+1,N)Dm+1=(wm+1,1,⋯,wm+1,i,⋯,wm+1,N)
wm+1,i=wm,iZmexp(−αmyiGm(xi))wm+1,i=wm,iZmexp(−αmyiGm(xi))
其中,ZmZm为规范化因子
Zm=∑i=1Nwm,i∗exp(−αmyiGm(xi))Zm=∑i=1Nwm,i∗exp(−αmyiGm(xi))
则得到最终分类器
sign(f(x))=sign(∑m=1MαmGm(x))sign(f(x))=sign(∑m=1MαmGm(x))
αmαm是emem的单调递减函数,特别地,当em≤12em≤12时,αm≥0αm≥0;当em>12em>12时,即基分类器不满足弱可学习的条件(比随机猜测好),则应该停止迭代。具体算法流程如下:
1D1(i)=1/ND1(i)=1/N% Initialize the weight distribution
2 form=1,⋯,Mm=1,⋯,M:
3 learn base classifierGm(x)Gm(x);
4 ifem>0.5em>0.5then break;
5 updateαmαmandDm+1Dm+1;
6 end for
在算法第4步,学习过程有可能停止,导致学习不充分而泛化能力较差。因此,可采用“重采样”(re-sampling)避免训练过程过早停止;即抛弃当前不满足条件的基分类器,基于重新采样的数据训练分类器,从而获得学习“重启动”机会。
AdaBoost能够自适应(addaptive)地调整样本的权值分布,将分错的样本的权重设高、分对的样本的权重设低;所以被称为“Adaptive Boosting”。sklearn的AdaBoostClassifier实现了AdaBoost,默认的基分类器是能fit()带权值样本的DecisionTreeClassifier。
老师木在微博上提出了关于AdaBoost的三个问题:
1,adaboost不易过拟合的神话。2,adaboost人脸检测器好用的本质原因,3,真的要求每个弱分类器准确率不低于50%
3. 参考资料
[1] Freund, Yoav, and Robert E. Schapire. "A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting." Journal of Computer and System Sciences 55.1 (1997): 119-139.
[2] 李航,《统计学习方法》.
[3] 周志华,《机器学习》.
[4] Pang-Ning Tan, Michael Steinbach, Vipin Kumar,Introduction to Data Mining.
[5] Ji Zhu,Classification.
[6] @龙星镖局,机器学习刀光剑影之 屠龙刀.
[7] 过拟合,为什么说bagging是减少variance,而boosting是减少bias?