一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法

一、理论基础

1、樽海鞘群优化算法

请参考这里。

2、改进的樽海鞘群优化算法

与其他元启发式算法类似，原SSA算法也存在收敛速度慢、容易陷入局部最优等缺点。为此本文从两个方面对其进行改进：首先，在种群个体更新时采用折射反向学习机制，从而提高种群多样性，避免算法陷入局部最优;其次，在追随者位置更新中引入自适应控制因子，进一步提高求解精度和收敛速度。

（1）折射反向学习机制

折射反向学习(Refracted Opposition-Based Learning,ROBL)是一种新型的算法改进机制，其本质是在反向学习的基础上，结合光的折射定律来寻找更优的候选解。近年被用于改进原粒子群优化算法与飞蛾扑火算法等，已被证明能够在不同程度上改善基本算法的性能。ROBL的具体数学原理请参考文献[1]。这里给出在SSA再改进的公式：$$x_{i,j}^{\ast }=\frac{a_j+b_j}{2}+\frac{a_j+b_j}{2k}-\frac{x_{i,j}}{k}\text{\hspace{1em}(1)}$$其中，$x_{i,j}$表示当前种群中第$i$个体在第$j$维上位置，$x_{i,j}^{\ast }$为$x_{i,j}$的折射反向解，$a_j,b_j$分别为搜索空间上第$j$维的最小值和最大值。

（2）自适应控制因子

本文提出将控制因子$c_1$引入追随者的位置更新，此时追随者也能够与引导者一样，产生自适应更新，从而提高算法跳出局部最优的能力，并加快整体的收敛速度。新的追随者公式为$$x_{i,j}=\frac{c_1}{2}(x_{i,j}+x_{i-1,j})\text{\hspace{1em}(2)}$$

（3）RCSSA算法

综合上述策略对基本SSA算法进行改进后，得到的RCSSA算法实现流程如下：
Step 1：设置算法参数：种群规模$N$，最大迭代次数$T$，搜索维数$D$，搜索范围$[lb,ub]$；随机生成樽海鞘种群；
Step 2：计算每个个体的适应度值，将适应度值最小的个体位置作为食物源；
Step 3：更新控制因子$c_1$，判断当前种群数是否超过$N/2$：超过则进入Step 5，否则进入Step 4；
Step 4：更新随机数$c_2,c_3$，更新每个引导者个体的位置，同时采用式(1)计算其折射反向解，比较二者适应度大小，取较小的一个个体作为新的位置，并进入Step 6；
Step 5：采用引入控制因子c_1的式(2)来更新每个追随者个体的位置，并计算其折射反向解，比较二者适应度大小，取较小的一个个体为新的位置；
Step 6：比较食物源和当前樽海鞘最优个体的适应度大小，取较小的一个为新的食物源；
Step 7：若当前迭代次数达到最大迭代次数$T$，则输出最优个体，即算法找到的最优解；否则，返回Step 2。

二、仿真实验与结果分析

利用RCSSA算法对23个基准测试函数进行寻优求解，并与基本SSA、仅加入折射反向学习机制的SSA算法(RSSA)以及仅采用自适应控制因子的SSA算法(CSSA)进行对比，以验证所提综合改进策略的效果。此外，选择了5种群智能算法进行对比测试，这5种算法分别为：PSO，GWO，WOA，多元宇宙优化算法(MVO)和正弦余弦算法(SCA)。
为了对比的公平性，将所有算法的参数设置为一致：迭代次数设为500，种群规模均设为30，控制因子初始值均设为2。其余算法参数按原论文进行取值，其中，RCSSA与RSSA中的缩放因子k=10000。独立运行30次。以F1、F2、F3为例。
下图为F1寻优的对比曲线。
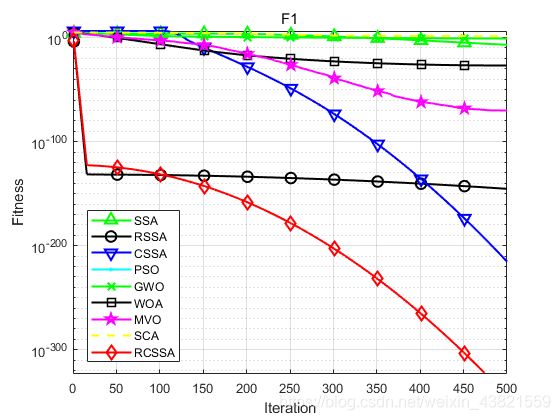9种算法对F1函数寻优的最大值、最小值、平均值及标准差如下所示：

函数：F1
SSA：最大值: 8.8452e-07,最小值:2.8193e-08,平均值1.2572e-07,标准差:1.6191e-07
RSSA：最大值: 5.988e-146,最小值:3.0939e-146,平均值4.3496e-146,标准差:5.667e-147
CSSA：最大值: 2.4874e-217,最小值:1.2946e-217,平均值1.7201e-217,标准差:0
PSO：最大值: 0.19683,最小值:0.035963,平均值0.11158,标准差:0.041565
GWO：最大值: 1.4386e-26,最小值:6.4863e-30,平均值1.4198e-27,标准差:2.701e-27
WOA：最大值: 2.2124e-69,最小值:3.2704e-89,平均值7.3823e-71,标准差:4.0392e-70
MVO：最大值: 2.0713,最小值:0.42499,平均值1.1223,标准差:0.37768
SCA：最大值: 311.2178,最小值:0.026935,平均值28.0026,标准差:61.5479
RCSSA：最大值: 0,最小值:0,平均值0,标准差:0

下图为F2寻优的对比曲线。
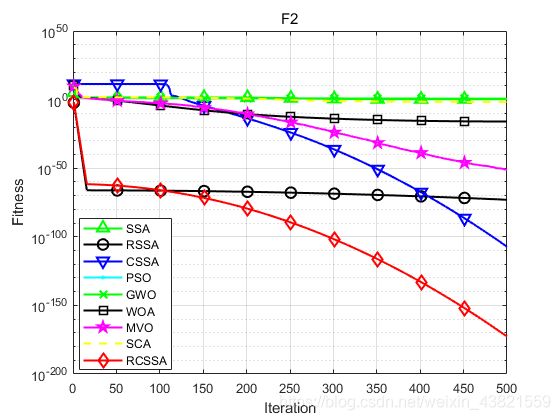9种算法对F2函数寻优的最大值、最小值、平均值及标准差如下所示：

函数：F2
SSA：最大值: 7.3722,最小值:0.033718,平均值1.7825,标准差:1.5009
RSSA：最大值: 1.2157e-73,最小值:8.1551e-74,平均值1.0135e-73,标准差:9.3303e-75
CSSA：最大值: 2.3741e-109,最小值:1.5298e-109,平均值1.9638e-109,标准差:2.2992e-110
PSO：最大值: 13.347,最小值:1.4553,平均值5.0527,标准差:2.853
GWO：最大值: 2.8264e-16,最小值:1.8844e-17,平均值1.1082e-16,标准差:6.8351e-17
WOA：最大值: 5.5959e-51,最小值:1.2914e-58,平均值6.2327e-52,标准差:1.3067e-51
MVO：最大值: 2.0343,最小值:0.41567,平均值0.90537,标准差:0.33768
SCA：最大值: 0.07071,最小值:5.912e-05,平均值0.019241,标准差:0.022942
RCSSA：最大值: 2.2982e-173,最小值:1.4374e-173,平均值1.8867e-173,标准差:0

下图为F3寻优的对比曲线。
9种算法对F3函数寻优的最大值、最小值、平均值及标准差如下所示：

函数：F3
SSA：最大值: 4847.6763,最小值:499.0865,平均值2223.7686,标准差:1132.344
RSSA：最大值: 3.9855e-145,最小值:6.6326e-146,平均值1.6626e-145,标准差:7.8808e-146
CSSA：最大值: 1.4113e-215,最小值:2.5987e-217,平均值2.2568e-216,标准差:0
PSO：最大值: 73.2788,最小值:11.7537,平均值34.6871,标准差:15.9091
GWO：最大值: 0.00016388,最小值:1.6624e-08,平均值1.3809e-05,标准差:3.5873e-05
WOA：最大值: 58392.852,最小值:29435.7149,平均值43614.7392,标准差:6559.6644
MVO：最大值: 636.9562,最小值:86.562,平均值237.1057,标准差:116.2842
SCA：最大值: 18522.7777,最小值:1250.9147,平均值7336.1166,标准差:5109.4863
RCSSA：最大值: 0,最小值:0,平均值0,标准差:0

结果表明：所提RCSSA算法可以有效提升原SSA算法的优化性能，其在整体性能上要明显优于GWO、WOA、SCA等多个当前最先进的群智能优化算法，并适用于处理高维函数优化问题。

三、参考文献

[1] 范千、陈振健、夏樟华. 一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法[J]. 哈尔滨工业大学学报, 2020, v.52(10):189-197.

四、Matlab仿真程序

原始SSA算法：

function [fitnessgbest, gbest, Curve] = SSA(X, N, Max_iter, lb, ub, dim, fobj)

%% SSA参数
% 计算适应度值
for i = 1:N
    fitness(i) = fobj(X(i, :));
end
% 初始化领导者的位置和适应度值
[bestfitness, bestindex] = min(fitness);
gbest= X(bestindex, :);
fitnessgbest = bestfitness;

%% 迭代寻优
for t = 1:Max_iter
    c1 = 2*exp(-(4*t/Max_iter)^2);      % Eq. (3.2) in the paper
    
    for i = 1:N
        
        if i <= N/2
            for j = 1:dim
                c2 = rand();
                c3 = rand();
                %%%%%%%%%%%%% % Eq. (3.1) in the paper %%%%%%%%%%%%%%
                if c3 < 0.5
                    X(i, j) = gbest(j)+c1*((ub-lb)*c2+lb);
                else
                    X(i, j) = gbest(j)-c1*((ub-lb)*c2+lb);
                end
                %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
            end
        else
            point1 = X(i-1, :);
            point2 = X(i, :);
            
            X(i, :) = (point2+point1)/2;  % Eq. (3.4) in the paper
        end
    end
    
    for i = 1:N
        % 边界处理
        X(i, X(i, :) > ub) = ub;
        X(i, X(i, :) < lb) = lb;
        % 计算适应度值
        fitness(i) = fobj(X(i, :));
        
        if fitness(i) < fitnessgbest
            gbest = X(i, :);
            fitnessgbest = fitness(i);
        end
    end
    
    Curve(t) = fitnessgbest;

    disp(['SSA: At iteration ', num2str(t), ' ,the best fitness is ', num2str(fitnessgbest)]);
end

下载地址：
https://download.csdn.net/download/weixin_43821559/18545653