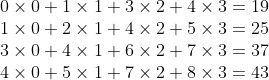如何理解卷积神经网络(CNN)中的卷积和池化?
目录
5.1 二维卷积层
5.1.1 二维互相关运算
5.1.2 二维卷积层
5.1.3 图像中物体边缘检测
5.1.4 通过数据学习核数组
5.1.5 互相关运算和卷积运算
5.1.6 特征图和感受野
5.2 填充和步幅
5.2.1 填充
5.2.2 步幅
5.4 池化层
5.4.1 二维最大池化层和平均池化层
5.4.2 填充和步幅
5.4.3 多通道
关于《动手学深度学习》这本书
相关推荐:深度学习
5.1 二维卷积层
卷积神经网络(convolutional neural network)是含有卷积层(convolutional layer)的神经网络。本章中介绍的卷积神经网络均使用最常见的二维卷积层。它有高和宽两个空间维度,常用来处理图像数据。本节中,我们将介绍简单形式的二维卷积层的工作原理。
5.1.1 二维互相关运算
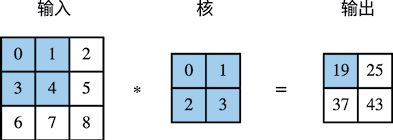
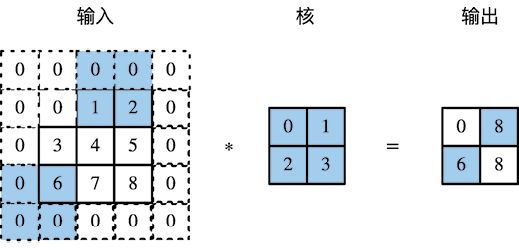
虽然卷积层得名于卷积(convolution)运算,但我们通常在卷积层中使用更加直观的互相关(cross-correlation)运算。在二维卷积层中,一个二维输入数组和一个二维核(kernel)数组通过互相关运算输出一个二维数组。我们用一个具体例子来解释二维互相关运算的含义。如图5-1所示,输入是一个高和宽均为3的二维数组。我们将该数组的形状记为3×3或(3, 3)。核数组的高和宽分别为2。该数组在卷积计算中又称卷积核或过滤器(filter)。卷积核窗口(又称卷积窗口)的形状取决于卷积核的高和宽,即2×2。图5-1中的阴影部分为第一个输出元素及其计算所使用的输入和核数组元素:0×0+1×1+3×2+4×3=19。
图5-1 二维互相关运算
在二维互相关运算中,卷积窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。当卷积窗口滑动到某一位置时,窗口中的输入子数组与核数组按元素相乘并求和,得到输出数组中相应位置的元素。图5-1中的输出数组的高和宽分别为2,其中的4个元素由二维互相关运算得出:
下面我们将上述过程实现在corr2d函数里。它接受输入数组X与核数组K,并输出数组Y。
In [1]: from mxnet import autograd, nd
from mxnet.gluon import nn
def corr2d(X, K): # 本函数已保存在d2lzh包中方便以后使用
h, w = K.shape
Y = nd.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
return Y 我们可以构造图5-1中的输入数组X、核数组K来验证二维互相关运算的输出。
In [2]: X = nd.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
K = nd.array([[0, 1], [2, 3]])
corr2d(X, K)
Out[2]:
[[19. 25.]
[37. 43.]]
5.1.2 二维卷积层
二维卷积层将输入和卷积核做互相关运算,并加上一个标量偏差来得到输出。卷积层的模型参数包括了卷积核和标量偏差。在训练模型的时候,通常我们先对卷积核随机初始化,然后不断迭代卷积核和偏差。
下面基于corr2d函数来实现一个自定义的二维卷积层。在构造函数__init__里,我们声明weight和bias这两个模型参数。前向计算函数forward则是直接调用corr2d函数再加上偏差。
In [3]: class Conv2D(nn.Block):
def __init__(self, kernel_size, **kwargs):
super(Conv2D, self).__init__(**kwargs)
self.weight = self.params.get('weight', shape=kernel_size)
self.bias = self.params.get('bias', shape=(1,))
def forward(self, x):
return corr2d(x, self.weight.data()) + self.bias.data()卷积窗口形状为p×q的卷积层称为p×q卷积层。同样,p×q卷积或p×q卷积核说明卷积核的高和宽分别为p和q。
5.1.3 图像中物体边缘检测
下面我们来看一个卷积层的简单应用——检测图像中物体的边缘,即找到像素变化的位置。首先我们构造一张6×8的图像(即高和宽分别为6像素和8像素的图像)。它中间4列为黑(0),其余为白(1)。
In [4]: X = nd.ones((6, 8))
X[:, 2:6] = 0
X
Out[4]:
[[1. 1. 0. 0. 0. 0. 1. 1.]
[1. 1. 0. 0. 0. 0. 1. 1.]
[1. 1. 0. 0. 0. 0. 1. 1.]
[1. 1. 0. 0. 0. 0. 1. 1.]
[1. 1. 0. 0. 0. 0. 1. 1.]
[1. 1. 0. 0. 0. 0. 1. 1.]]
然后我们构造一个高和宽分别为1和2的卷积核K。当它与输入做互相关运算时,如果横向相邻元素相同,输出为0;否则输出为非0。
In [5]: K = nd.array([[1, -1]])下面将输入X和我们设计的卷积核K做互相关运算。可以看出,我们将从白到黑的边缘和从黑到白的边缘分别检测成了1和-1。其余部分的输出全是0。
In [6]: Y = corr2d(X, K)
Y
Out[6]:
[[ 0. 1. 0. 0. 0. -1. 0.]
[ 0. 1. 0. 0. 0. -1. 0.]
[ 0. 1. 0. 0. 0. -1. 0.]
[ 0. 1. 0. 0. 0. -1. 0.]
[ 0. 1. 0. 0. 0. -1. 0.]
[ 0. 1. 0. 0. 0. -1. 0.]]
由此,我们可以看出,卷积层可通过重复使用卷积核有效地表征局部空间。
5.1.4 通过数据学习核数组
最后我们来看一个例子,它使用物体边缘检测中的输入数据X和输出数据Y来学习我们构造的核数组K。我们首先构造一个卷积层,将其卷积核初始化成随机数组。接下来在每一次迭代中,我们使用平方误差来比较Y和卷积层的输出,然后计算梯度来更新权重。简单起见,这里的卷积层忽略了偏差。
虽然我们之前构造了Conv2D类,但由于corr2d使用了对单个元素赋值([i, j]=)的操作因而无法自动求梯度。下面我们使用Gluon提供的Conv2D类来实现这个例子。
In [7]: # 构造一个输出通道数为1(将在5.3节介绍通道), 核数组形状是(1, 2)的二维卷积层
conv2d = nn.Conv2D(1, kernel_size=(1, 2))
conv2d.initialize()
# 二维卷积层使用4维输入输出, 格式为(样本, 通道, 高, 宽), 这里批量大小(批量中的样本数)和通
# 道数均为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
for i in range(10):
with autograd.record():
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
l.backward()
# 简单起见, 这里忽略了偏差
conv2d.weight.data()[:] -= 3e-2 * conv2d.weight.grad()
if (i + 1) % 2 == 0:
print('batch %d, loss %.3f' % (i + 1, l.sum().asscalar()))
batch 2, loss 4.949
batch 4, loss 0.831
batch 6, loss 0.140
batch 8, loss 0.024
batch 10, loss 0.004 可以看到,10次迭代后误差已经降到了一个比较小的值。现在来看一下学习到的核数组。
In [8]: conv2d.weight.data().reshape((1, 2))
Out[8]:
[[ 0.9895 -0.9873705]]
可以看到,学习到的核数组与我们之前定义的核数组K较接近。
5.1.5 互相关运算和卷积运算
实际上,卷积运算与互相关运算类似。为了得到卷积运算的输出,我们只需将核数组左右翻转并上下翻转,再与输入数组做互相关运算。可见,卷积运算和互相关运算虽然类似,但如果它们使用相同的核数组,对于同一个输入,输出往往并不相同。
那么,你也许会好奇卷积层为何能使用互相关运算替代卷积运算。其实,在深度学习中核数组都是学习出来的:卷积层无论使用互相关运算或卷积运算都不影响模型预测时的输出。为了解释这一点,假设卷积层使用互相关运算学习出图5-1中的核数组。设其他条件不变,使用卷积运算学习出的核数组即图5-1中的核数组按上下、左右翻转。也就是说,图5-1中的输入与学习出的已翻转的核数组再做卷积运算时,依然得到图5-1中的输出。为了与大多数深度学习文献一致,如无特别说明,本书中提到的卷积运算均指互相关运算。
5.1.6 特征图和感受野
二维卷积层输出的二维数组可以看作输入在空间维度(宽和高)上某一级的表征,也叫特征图(feature map)。影响元素x的前向计算的所有可能输入区域(可能大于输入的实际尺寸)叫作x的感受野(receptive field)。以图5-1为例,输入中阴影部分的4个元素是输出中阴影部分元素的感受野。我们将图5-1中形状为2×2的输出记为Y,并考虑一个更深的卷积神经网络:将Y与另一个形状为2×2的核数组做互相关运算,输出单个元素z。那么,z在Y上的感受野包括Y的全部4个元素,在输入上的感受野包括其中全部9个元素。可见,我们可以通过更深的卷积神经网络使特征图中单个元素的感受野变得更加广阔,从而捕捉输入上更大尺寸的特征。
我们常使用“元素”一词来描述数组或矩阵中的成员。在神经网络的术语中,这些元素也可称为“单元”。当含义明确时,本书不对这两个术语做严格区分。
5.2 填充和步幅
在5.1节的例子里,我们使用高和宽为3的输入与高和宽为2的卷积核得到高和宽为2的输出。一般来说,假设输入形状是
![]()
,卷积核窗口形状是
![]()
,那么输出形状将会是
![]()
所以卷积层的输出形状由输入形状和卷积核窗口形状决定。本节我们将介绍卷积层的两个超参数,即填充和步幅。它们可以对给定形状的输入和卷积核改变输出形状。
5.2.1 填充
填充(padding)是指在输入高和宽的两侧填充元素(通常是0元素)。图5-2里我们在原输入高和宽的两侧分别添加了值为0的元素,使得输入高和宽从3变成了5,并导致输出高和宽由2增加到4。图5-2中的阴影部分为第一个输出元素及其计算所使用的输入和核数组元素:
![]()
。
图5-2 在输入的高和宽两侧分别填充了0元素的二维互相关计算
一般来说,如果在高的两侧一共填充ph行,在宽的两侧一共填充pw列,那么输出形状将会是
![]()
也就是说,输出的高和宽会分别增加ph和pw。
在很多情况下,我们会设置
![]()
和
![]()
来使输入和输出具有相同的高和宽。这样会方便在构造网络时推测每个层的输出形状。假设这里kh是奇数,我们会在高的两侧分别填充
![]()
行。如果kh是偶数,一种可能是在输入的顶端一侧填充
![]()
行,而在底端一侧填充
![]()
行。在宽的两侧填充同理。
卷积神经网络经常使用奇数高和宽的卷积核,如1、3、5和7,所以两端上的填充个数相等。对任意的二维数组X,设它的第i行第j列的元素为X[i, j]。当两端上的填充个数相等,并使输入和输出具有相同的高和宽时,我们就知道输出Y[i, j]是由输入以X[i, j]为中心的窗口同卷积核进行互相关计算得到的。
下面的例子里我们创建一个高和宽为3的二维卷积层,然后设输入高和宽两侧的填充数分别为1。给定一个高和宽为8的输入,我们发现输出的高和宽也是8。
In [1]: from mxnet import nd
from mxnet.gluon import nn
# 定义一个函数来计算卷积层。它初始化卷积层权重, 并对输入和输出做相应的升维和降维
def comp_conv2d(conv2d, X):
conv2d.initialize()
# (1, 1)代表批量大小和通道数(5.3节将介绍)均为1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
return Y.reshape(Y.shape[2:]) # 排除不关心的前两维:批量和通道
# 注意这里是两侧分别填充1行或列, 所以在两侧一共填充2行或列
conv2d = nn.Conv2D(1, kernel_size=3, padding=1)
X = nd.random.uniform(shape=(8, 8))
comp_conv2d(conv2d, X).shape
Out[1]: (8, 8)当卷积核的高和宽不同时,我们也可以通过设置高和宽上不同的填充数使输出和输入具有相同的高和宽。
In [2]: # 使用高为5、宽为3的卷积核。在高和宽两侧的填充数分别为2和1
conv2d = nn.Conv2D(1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape
Out[2]: (8, 8)5.2.2 步幅
在5.1节里我们介绍了二维互相关运算。卷积窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。我们将每次滑动的行数和列数称为步幅(stride)。
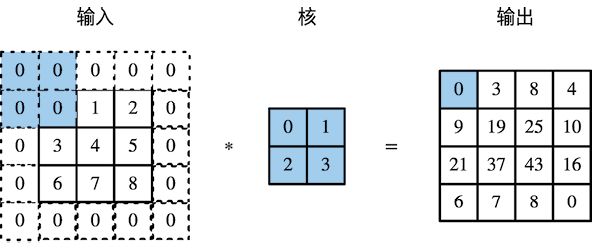
目前我们看到的例子里,在高和宽两个方向上步幅均为 1。我们也可以使用更大步幅。图 5-3 展示了在高上步幅为 3、在宽上步幅为 2 的二维互相关运算。可以看到,输出第一列第二个元素时,卷积窗口向下滑动了3行,而在输出第一行第二个元素时卷积窗口向右滑动了2列。当卷积窗口在输入上再向右滑动2列时,由于输入元素无法填满窗口,无结果输出。图5-3中的阴影部分为输出元素及其计算所使用的输入和核数组元素:
![]()
、
![]()
。
图5-3 高和宽上步幅分别为3和2的二维互相关运算
一般来说,当高上步幅为
![]()
,宽上步幅为
![]()
时,输出形状为
![]()
如果设置
![]()
和
![]()
,那么输出形状将简化为
![]()
。更进一步,如果输入的高和宽能分别被高和宽上的步幅整除,那么输出形状将是
![]()
。
下面我们令高和宽上的步幅均为2,从而使输入的高和宽减半。
In [3]: conv2d = nn.Conv2D(1, kernel_size=3, padding=1, strides=2)
comp_conv2d(conv2d, X).shape
Out[3]: (4, 4)接下来是一个稍微复杂点儿的例子。
In [4]: conv2d = nn.Conv2D(1, kernel_size=(3, 5), padding=(0, 1), strides=(3, 4))
comp_conv2d(conv2d, X).shape
Out[4]: (2, 2)为了表述简洁,当输入的高和宽两侧的填充数分别为
![]()
和
![]()
时,我们称填充为
![]()
。特别地,当
![]()
时,填充为p。当在高和宽上的步幅分别为
![]()
和
![]()
时,我们称步幅为
![]()
。特别地,当
![]()
时,步幅为s。在默认情况下,填充为0,步幅为1。
小结
- 填充可以增加输出的高和宽。这常用来使输出与输入具有相同的高和宽。
- 步幅可以减小输出的高和宽,例如输出的高和宽仅为输入的高和宽的1/n(n为大于1的整数)。
5.4 池化层
回忆一下,在5.1节里介绍的图像物体边缘检测应用中,我们构造卷积核从而精确地找到了像素变化的位置。设任意二维数组X的i行j列的元素为X[i, j]。如果我们构造的卷积核输出Y[i, j]=1,那么说明输入中X[i, j]和X[i, j+1]数值不一样。这可能意味着物体边缘通过这两个元素之间。但实际图像里,我们感兴趣的物体不会总出现在固定位置:即使我们连续拍摄同一个物体也极有可能出现像素位置上的偏移。这会导致同一个边缘对应的输出可能出现在卷积输出Y中的不同位置,进而对后面的模式识别造成不便。
在本节中我们介绍池化(pooling)层,它的提出是为了缓解卷积层对位置的过度敏感性。
5.4.1 二维最大池化层和平均池化层
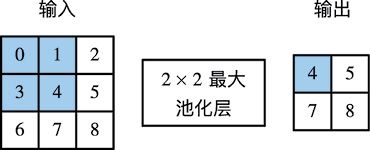
同卷积层一样,池化层每次对输入数据的一个固定形状窗口(又称池化窗口)中的元素计算输出。不同于卷积层里计算输入和核的互相关性,池化层直接计算池化窗口内元素的最大值或者平均值。该运算也分别叫作最大池化或平均池化。在二维最大池化中,池化窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。当池化窗口滑动到某一位置时,窗口中的输入子数组的最大值即输出数组中相应位置的元素。
图5-6 池化窗口形状为2 × 2的最大池化
图5-6展示了池化窗口形状为2×2的最大池化,阴影部分为第一个输出元素及其计算所使用的输入元素。输出数组的高和宽分别为2,其中的4个元素由取最大值运算max得出:
二维平均池化的工作原理与二维最大池化类似,但将最大运算符替换成平均运算符。池化窗口形状为
![]()
的池化层称为
![]()
池化层,其中的池化运算叫作
![]()
池化。
让我们再次回到本节开始提到的物体边缘检测的例子。现在我们将卷积层的输出作为2×2最大池化的输入。设该卷积层输入是X、池化层输出为Y。无论是X[i, j]和X[i, j+1]值不同,还是X[i, j+1]和X[i, j+2]不同,池化层输出均有Y[i, j]=1。也就是说,使用2×2最大池化层时,只要卷积层识别的模式在高和宽上移动不超过一个元素,我们依然可以将它检测出来。
下面把池化层的前向计算实现在pool2d函数里。它与5.1节里corr2d函数非常类似,唯一的区别在计算输出Y上。
In [1]: from mxnet import nd
from mxnet.gluon import nn
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = nd.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y 我们可以构造图5-6中的输入数组X来验证二维最大池化层的输出。
In [2]: X = nd.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
pool2d(X, (2, 2))
Out[2]:
[[4. 5.]
[7. 8.]]
同时我们实验一下平均池化层。
In [3]: pool2d(X, (2, 2), 'avg')
Out[3]:
[[2. 3.]
[5. 6.]]
5.4.2 填充和步幅
同卷积层一样,池化层也可以在输入的高和宽两侧的填充并调整窗口的移动步幅来改变输出形状。池化层填充和步幅与卷积层填充和步幅的工作机制一样。我们将通过nn模块里的二维最大池化层MaxPool2D来演示池化层填充和步幅的工作机制。我们先构造一个形状为(1, 1, 4, 4)的输入数据,前两个维度分别是批量和通道。
In [4]: X = nd.arange(16).reshape((1, 1, 4, 4))
X
Out[4]:
[[[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]]]]
默认情况下,MaxPool2D实例里步幅和池化窗口形状相同。下面使用形状为(3, 3)的池化窗口,默认获得形状为(3, 3)的步幅。
In [5]: pool2d = nn.MaxPool2D(3)
pool2d(X) # 因为池化层没有模型参数, 所以不需要调用参数初始化函数
Out[5]:
[[[[10.]]]]
我们可以手动指定步幅和填充。
In [6]: pool2d = nn.MaxPool2D(3, padding=1, strides=2)
pool2d(X)
Out[6]:
[[[[ 5. 7.]
[13. 15.]]]]
当然,我们也可以指定非正方形的池化窗口,并分别指定高和宽上的填充和步幅。
In [7]: pool2d = nn.MaxPool2D((2, 3), padding=(1, 2), strides=(2, 3))
pool2d(X)
Out[7]:
[[[[ 0. 3.]
[ 8. 11.]
[12. 15.]]]]
5.4.3 多通道
在处理多通道输入数据时,池化层对每个输入通道分别池化,而不是像卷积层那样将各通道的输入按通道相加。这意味着池化层的输出通道数与输入通道数相等。下面我们将数组X和X+1在通道维上连结来构造通道数为2的输入。
In [8]: X = nd.concat(X, X + 1, dim=1)
X
Out[8]:
[[[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]]
[[ 1. 2. 3. 4.]
[ 5. 6. 7. 8.]
[ 9. 10. 11. 12.]
[13. 14. 15. 16.]]]]
池化后,我们发现输出通道数仍然是 2。
In [9]: pool2d = nn.MaxPool2D(3, padding=1, strides=2)
pool2d(X)
Out[9]:
[[[[ 5. 7.]
[13. 15.]]
[[ 6. 8.]
[14. 16.]]]]
关于《动手学深度学习》这本书
- 人工智能机器学习领域重磅入门自学教程,交互式实战环境学习的全新模式
- 原理+实战,配套网站提供Pytorch和TensorFlow代码,提供视频教
本书旨在向读者交付有关深度学习的交互式学习体验。书中不仅阐述深度学习的算法原理,还演示它们的实现和运行。与传统图书不同,本书的每一节都是一个可以下载并运行的 Jupyter记事本,它将文字、公式、图像、代码和运行结果结合在了一起。此外,读者还可以访问并参与书中内容的讨论。
全书的内容分为3个部分:第一部分介绍深度学习的背景,提供预备知识,并包括深度学习基础的概念和技术;第二部分描述深度学习计算的重要组成部分,还解释近年来令深度学习在多个领域大获成功的卷积神经网络和循环神经网络;第三部分评价优化算法,检验影响深度学习计算性能的重要因素,并分别列举深度学习在计算机视觉和自然语言处理中的重要应用。
本书同时覆盖深度学习的方法和实践,主要面向在校大学生、技术人员和研究人员。阅读本书需要读者了解基本的Python编程或附录中描述的线性代数、微分和概率基础。
相关推荐:深度学习
- 深度学习领域奠基性经典畅销书,数据科学家和机器学习从业者必读
- 长期位居美亚AI和机器学习类图书榜首,图灵奖获奖作品,全彩印刷
AI圣经!深度学习领域奠基性的经典畅销书!长期位居美国ya马逊AI和机器学习类图书榜首!所有数据科学家和机器学习从业者的bi读图书!特斯拉CEO埃隆·马斯克等国内外众多专家推jian!
深度学习是机器学习的一个分支,它能够使计算机通过层次概念来学习经验和理解世界。因为计算机能够从经验中获取知识,所以不需要人类来形式化地定义计算机需要的所有知识。层次概念允许计算机通过构造简单的概念来学习复杂的概念,而这些分层的图结构将具有很深的层次。本书会介绍深度学习领域的许多主题。
本书囊括了数学及相关概念的背景知识,包括线性代数、概率论、信息论、数值优化以及机器学习中的相关内容。同时,它还介绍了工业界中实践者用到的深度学习技术,包括深度前馈网络、正则化、优化算法、卷积网络、序列建模和实践方法等,并且调研了诸如自然语言处理、语音识别、计算机视觉、在线推荐系统、生物信息学以及视频游戏方面的应用。最后,本书还提供了一些研究方向,涵盖的理论主题包括线性因子模型、自编码器、表示学习、结构化概率模型、蒙特卡罗方法、配分函数、近似推断以及深度生成模型。