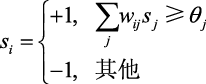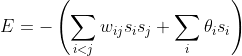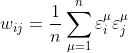最简单的神经网络:霍普菲尔德神经网络
霍普菲尔德神经网络[1]也许是最简单的神经网络,因为它是一个完全连接的单层自动关联神经网络。换言之,它只有一层,其中每个神经元都彼此相连。此外,术语“自动关联”是指神经网络在识别出模式后会返回整个模式,神经网络将补全不完整模式或失真模式。
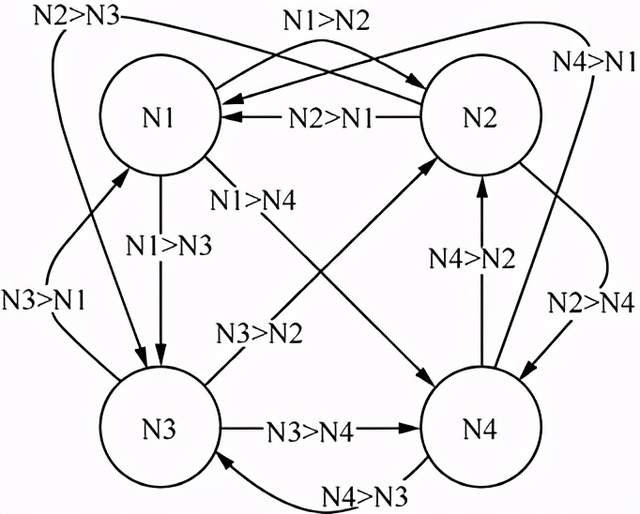
图3-1展示了只有4个神经元的霍普菲尔德神经网络。四神经元网络非常方便,因为它足够小,方便可视化,且可以识别一些模式。
图3-1 具有12个连接的霍普菲尔德神经网络
因为霍普菲尔德神经网络中的每个神经元都彼此相连,所以你可能会假设四神经元网络将包含4×4的矩阵,即16个连接。但是,16个连接要求每个神经元与其自身和每个其他神经元都连接。在霍普菲尔德神经网络中,不会有16个连接,其实际的连接数为12。
这些连接被加权并存储在矩阵中。4×4的矩阵将存储图3-1所示的网络。实际上,这个矩阵的对角线是0,因为没有自连接。本书中的所有神经网络示例都将使用某种形式的矩阵来存储其权重。
霍普菲尔德神经网络中的每个神经元的状态为真(1)或假(−1)。这些状态最初是霍普菲尔德神经网络的输入,最终成为神经网络的输出。要确定霍普菲尔德神经元的状态是−1还是1,请使用公式3-1:
(3-1)
公式3-1计算神经元
![]()
的状态。给定神经元的状态很大程度上取决于其他神经元的状态。该公式将其他神经元(
![]()
)的权重(
![]()
)和状态(
![]()
)相乘并进行累加。本质上,如果此总和大于阈值(θ),则当前神经元(
![]()
)的状态为+1,否则为−1。阈值通常为0。
由于单个神经元的状态取决于其他神经元的状态,因此该公式计算神经元的顺序非常重要。程序员经常采用以下两种策略来计算霍普菲尔德神经网络中所有神经元的状态。
- 异步:这种策略一次仅更新一个神经元。它随机选择神经元。
- 同步:它同时更新所有神经元。该方法不太符合现实世界,因为生物有机体缺乏使神经元同步的全局时钟。
通常,你应该运行一个霍普菲尔德神经网络,直到所有神经元的状态稳定下来。尽管每个神经元的状态都依赖于其他神经元的状态,但神经网络通常会收敛到稳定状态。
重要的是要对神经网络收敛到稳定状态的距离有一些指标。你可以计算霍普菲尔德神经网络的能量值。随着霍普菲尔德神经网络转向更稳定的状态,该值逐步减小。要评估神经网络的稳定性,可以使用能量函数。公式3-2展示了能量函数:
(3-2)
本章后面要讨论的玻尔兹曼机也利用了这种能量函数。玻尔兹曼机与霍普菲尔德神经网络具有许多相似之处。当阈值为0时,公式3-2中等号右边的第二项就会消失。清单3-1包含实现公式3-2的代码。
清单3-1 霍普菲尔德能量
def energy(weights,state,threshold):
# First term
a = 0
for i in range(neuron_count):
for j in range(neuron_count):
a = a + weight[i][j] * state[i] * state[j]
a = a * -0.5
# Second term
b = 0
for i in range(neuron_count):
b = b + state[i] * threshold[i]
# Result
return a + b训练霍普菲尔德神经网络
你可以训练霍普菲尔德神经网络安排其权重,使得该神经网络收敛到所需模式(也称为训练集)。
这些期望的模式是一个模式列表,对于构成玻尔兹曼机的每个神经元有一个布尔值。以下数据可能代表具有8个神经元的霍普菲尔德神经网络的一个训练集,包含4个模式:
1 1 0 0 0 0 0 0
0 0 0 0 1 1 0 0
1 0 0 0 0 0 0 1
0 0 0 1 1 0 0 0以上数据完全是任意的。但是,它们确实代表了训练霍普菲尔德神经网络的实际模式。训练后,类似于下面的模式应该与训练集中的一个近似的模式匹配:
1 1 1 0 0 0 0 0因此,霍普菲尔德神经网络的状态应变更为以下模式:
1 1 0 0 0 0 0 0你可以通过Hebbian[2]或Storkey[3]学习来训练霍普菲尔德神经网络。Hebbian学习过程在生物学上是合理的,通常表示为“细胞如果一起激活,就连接在一起”。换言之,如果两个神经元经常对相同的输入刺激做出反应,则它们将被连接起来。公式3-3从数学上总结了这种行为:
(3-3)
常数
![]()
代表训练集元素ε(epsilon)的数量。权重矩阵是方阵,包含等于神经元数量的行和列。对角线元素总是0,因为神经元未与其自身连接。矩阵中的其他位置将包含一些值,指定训练模式中两个值是+1或−1的概率。清单3-2包含了实现公式3-3的代码。
清单3-2 霍普菲尔德的Hebbian训练
def add_pattern(weights,pattern,n):
for i in range(neuron_count):
for j in range(neuron_count):
if i==j:
weights[i][j] = 0
else:
weights[i][j] = weights[i][j]
+((pattern[i] * pattern[j])/n)我们应用add_pattern方法来添加每个训练元素。参数weights指定权重矩阵,参数pattern指定每个单独的训练元素,参数n指定训练集中的元素数量。
公式和代码可能不足以展示从输入模式生成权重的过程。为了让这个过程可视化,我们在以下网址提供了一个在线JavaScript应用程序:
http://www.heatonresearch.com/aifh/vol3/hopfield.html考虑将以下数据用于训练霍普菲尔德神经网络:
[1, 0, 0, 1]
[0, 1, 1, 0]上述数据应生成如图3-2所示的权重矩阵。
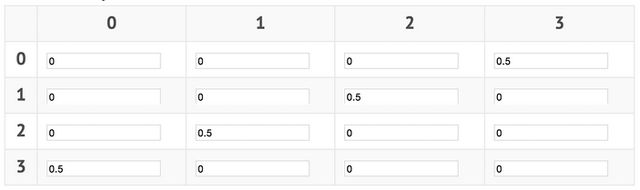
图3-2 权重矩阵
要计算上述矩阵,用1除以训练集元素的数量,结果是1/2,即0.5。值0.5放置在训练集中包含1的每个行列位置上。如第一个训练元素在神经元#0和#3中的值为1,则将0.5添加到第0行第3列和第3行第0列。对于其他训练集元素,继续执行相同的过程。
霍普菲尔德神经网络的另一种常见训练算法是Storkey算法。与刚刚描述的Hebbian算法相比,由Storkey算法训练的霍普菲尔德神经网络的模式能力更强。Storkey算法比Hebbian算法更复杂。
Storkey算法的第一步是计算一个名为“本地字段”(local field)的值。利用公式3-4计算该值:
(3-4)
我们针对每个权重元素(
![]()
和
![]()
)计算本地字段值(
![]()
)。和以前一样,我们使用权重(
![]()
)和训练集元素(
![]()
)。清单3-3提供了计算本地字段的代码。
清单3-3 计算Storkey本地字段
def calculate_local_field(weights, i, j, pattern):
sum = 0
for k in range(len(pattern)):
if k != i:
sum = sum + weights[i][k] * pattern[k]
return sum公式3-5利用本地字段值计算所需的变化:
(3-5)
清单3-4计算了权重增量的值。
清单3-4 计算权重增量
def add_pattern(weights, pattern):
sum_matrix = matrix(len(pattern),len(pattern))
n = len(pattern)
for i in range(n):
for j in range(n):
t1 = (pattern[i] * pattern[j])/n
t2 = (pattern[i] *
calculate_local_field(weights,j,i,pattern))/n
t3 = (pattern[j] *
calculate_local_field(weights,i,j,pattern))/n
d = t1-t2-t3;
sum_matrix[i][j] = sum_matrix[i][j] + d
return sum_matrix一旦计算了权重增量,就可以将它们添加到已有的权重矩阵中。如果还没有权重矩阵,只需让增量权重矩阵成为权重矩阵即可。
本文摘自:《人工智能算法(卷3):深度学习和神经网络》
本书是介绍AI的系列图书中的卷3。AI是一个涵盖许多子学科的、研究广泛的领域。对没有读过本系列图书卷1或卷2的读者,本书简介将提供一些背景信息。读者无须在阅读本书之前先阅读卷1或卷2。
本书将演示各种现实世界任务中的神经网络,如图像识别和数据科学。我们研究了当前的神经网络技术,包括ReLU激活、随机梯度下降、交叉熵、正则化、Dropout及可视化等。
本书适合作为人工智能入门读者以及对人工智能算法感兴趣的读者阅读参考。