统计基础三

1. 样本均值(sample mean)

是在总体中的样本数据的均值，均值均值是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标，样本均值是总体均值的点估计(point estimator)

n是样本数， 表示第i个x的值

# 均值
pd.DataFarme.mean()
np.mean(data)

from scipy import stats
# 使用t检验
# 第二个为p值

# 可以进行单样本T检验
stats.ttest_1sampl(a=检测数据，popmean=假设值，axis=0, nan_policy='propagate')
# nan_policy default return nan

# 检验两个独立样本的均值是否存在显著差异
stats.ttest_ind(a=样本数据1, b=样本数据2, equal_var=True)
equal_var可以用检测方差齐性来判断

检验两个配对样本的均值是否存在显著差异

stats.ttest_rel(sample1, sample2)

2 样本方差(sample variance)

在许多实际情况下，数据的真实差异事先是不知道的，必须以某种方式计算。 当处理非常大的数据时时，不可能对真实数据集中的数据进行处理，需要抽取一些样本计算其方差，也就是每一个数据与其总体均值的距离的平均数。而且样本方差是总体方差的点估计(无偏估计):

n是样本数， 表示第i个x的值，总体均值

均值
pd.DataFarme.var() # 默认ddof=1
np.var(data, ddof=1) # 默认ddof=0

检验方差齐性
from scipy import stats
# p_val > 0.05 则表示齐性
# 返回的第二个值为p值

stats.bartlett(sample1, sample2,....)
# 但是需要具有正太性

stats.levene(sample1, sample2, sample3,...., center='median', proportiontocut=.05)
# center{‘mean’, ‘median’, ‘trimmed’}

stats.fligner(sample1, sample2,..., center='median', proportiontocut=0.05)
# 非参数检验，也不依赖分布

3. 标准差系数

当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响，而变异系数可以做到这一点，它是原始数据标准差与原始数据平均数的比。这样就可以进行客观比较了。事实上，可以认为变异系数和极差、标准差和方差一样，都是反映数据离散程度的绝对值。其数据大小不仅受变量值离散程度的影响，而且还受变量值平均水平大小的影响。简单的说：概率分布离散程度的归一化

n是样本数， 表示标准差，均值

pd.Series.std() \ pd.Series.mean()

stats.variation(sample)

# 以上对一组数据计算，略有细小偏差

4. 样本阶

是样本的数字特征，他们是模拟总体数字特征构造的，称为样本矩。样本矩主要包括样本均值、未修正样本方差(总体方差)、样本（修正）方差(样本方差)、样本k阶原点矩和样本k阶中心距

样本k阶原点矩是随机变量x'偏离'原点(0,0)的'距离'的k次方的期望值，1阶原点矩是数学期望

n是样本数， 第i个x的值的k方

样本k阶中心矩是随机变量x'偏离'中心(均值)的'距离'的k次方的期望值，2阶中心矩是方差；3阶（中心）矩表示 偏斜度； 4阶（中心）矩表示 峰度；

n是样本数， 第i个x的值的k方, 为均值

5. 样本峰度(sample kurtosis)和样本偏斜(sample skewness)

样本峰度是 4阶（中心）矩/方差平方

# pandas 
pandas.Series.kurt()
# stats
stats.kurtosis(a=sample, axis=0)

stats.kurtosistest(a=sample, axis=0, nan_policy='propagate')
# default returns nan
# pvalue 双侧检验 检验峰度是否符合正态分布的峰度
# 只对样本>20有效

样本偏斜是 3阶（中心）矩

# pandas 
pandas.Series.skew()
# stats
stats.skew(a=sample, axis=0， bias=True, nan_policy='propagate')
# nan_policy return nan default
# 对于正太数据和所有数据都相等 return 0
# > 0 是高峰左移, 右偏，正偏， < 0高峰右移，左偏，负偏

stats.skewtest(a=sample, axis=0, nan_policy='propagate')
# nan_policy return nan default

# 样本>18
# pvalue 双侧检验 检验偏度是否符合正态分布的峰度


# 检验正态分布
stats.normaltest(a, axis=0, nan_policy='propagate')
# nan_policy return nan default
# 样本 > 8
# 双侧检验偏度是否符合正态分布

6 次序统计量(Ordered Statistics)

设是取自总体X的子样本， 称为该样本的观测值，从小到大排列用，即 ，如果有两个值是相等的，他们先后次序是可以任意安排。第i个次序统计量是子样本不管是哪一组，其取得的观测值总是其中为观测值。

对于容量为n的子样本可得到n个次序统计量，其中：
　　　- 最小次序统计量
　　　- 最大次序统计量
　　　- 极差：
　　　- 四分卫极差：
　　　- 中位数：
　　　　　　奇数: X_(m+1)
　　　　　　偶数: (X_(m+1) + X_(m))/2

给定任意随机变量
如果样本 是独立同分布的，而次序统计量是独立但不一定同分布。次序统计量的CDF(遵循二项分布)：

r：第r个次序统计量

对于最大值和最小值的CDF：

1. 前言

数据的集中趋势、离散程度和分布形态是了解数据和进行数据分析的基础。实际上数据总体不是够轻易得到的，即使能够得到，数据分析的成本巨大且效率低。因此，通过样本推导总体成为首选。在推断统计学中定距数据、定比数据的特性决定了它们是最适合进行推断分析的数据，描述数据的三个维度主要也是针对定距数据和定比数据进行的

从样本推断总体，最重要的就是通过样本的描述性统计指标推断总体的描述性统计指标，也就是表现总体的集中趋势、离散程度和分布形态，从而还原出总体数据的形象。描述性统计指标也被称为参数，而连接样本参数和总体参数的桥梁就是：抽样分布

抽样方式
从

• 无限总体进行抽样（N>= n*50倍以上）以及 从有限总体进行有放回抽样
  因为样本是无限多，可以抽取有限但大量的样本，由这些样本参数组
  成的概率分布也是抽样分布

• 从有限总体进行无放回抽样
  尽量全测量，样本推断总体存在误差。全测量得到的所有样本参数组成的概率分布就是其抽样分布。

均值抽样的性质
均值抽样的均值或数学期望等于总体均值，那么其均值是总体均值的无偏估计

均值分布的标准差在实际中计算很麻烦，如果已知总体标准差可以来推断均值样本分布的标准差
有限总体：

无限总体

在有限总体中当(N/n>20)那么修正因子的值将近似等于1，上述两个计算式相等，即有限总体无放回抽样的情况可以省略修正因子

中心极限理论

给定一个任意分布的总体。每次从这些总体中随机抽取 n(n>=30) 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布

Z分布

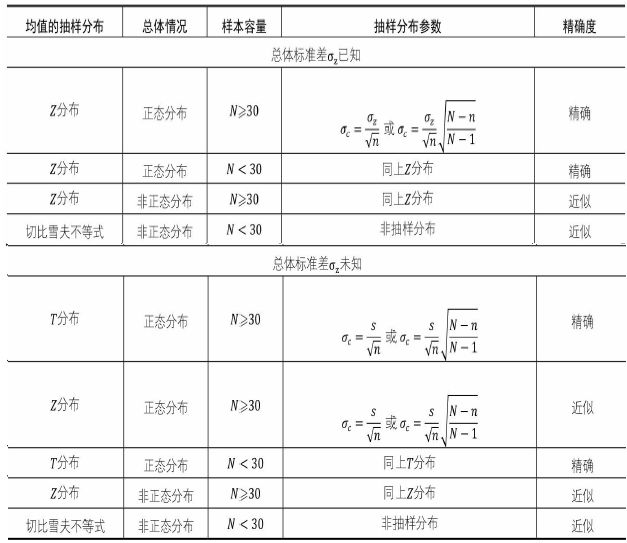
转换成标准正态分布的均值抽样分布称为Z分布，而均值抽样分布服从正态分布有两种情况：
　　1. 抽样的总体是正态分布, 样本容量没有要求
　　2. 是任意分布的总体，根据中心极限定理，当样本容量n大于或等于30时，均值的抽样分布也会服从正态分布
Z统计量就是普通正态分布转换成标准正态分布的公式。

可以通过Z分布通过样本信息推断总体均值，运用到总体参数估计和假设检验中

T分布

不同于Z分布，用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知（例如在样本数量足够多时），则应该用正态分布来估计总体均值(Z分布)。其统计量为:

：样本均值，s样本标准差，：总体均值，v：自由度，n：样本容量，t：T统计量值

如果已知等待分析的总体服从正态分布，从总体中抽取容量为n的所有可能样本，对每个样本都计算出它们相应的T统计量，则所有T统计量的值将组成一个连续型概率分布，这个分布就是T分布，T分布的
概率密度函数为

t:T统计量；v：自由度，n-1；·c为常数，使T分布函数曲线下的面积等于1

如果总体服从正态分布，总体标
准差未知，样本容量小于30，那么样本均值的抽样分布服从T～t（n-
1）的T分布；如果总体服从正态分布，总体标准差未知，样本容量大于或等于30时，那么样本均值的抽样分布不仅服从T～t（n-1）的T分布，而且还可以用Z分布来近似表达

切比雪夫定理

是一个统计规律，可以继续补充均值抽样分布。假设数据集合，其均值,标准差,对任意常数k>=1，位于区间内的数据比例会大于等于1-，即。并且无论是对称分布、有偏斜的分布还是多峰分布，切比雪夫不等式都成立。如果数据集合只是来自总体的一个随机样本，那么样本均值等于总体均值，样
本标准差s是总体标准差的合理估计，切比雪夫不等式还可以表示为：

均值抽样分布

卡方分布

卡方统计量：是一个随机变量，它能够表明样本方差和总体方差之间的比值关系。卡方统计量决定的抽样分布就是卡方分

代表样本方差；· 代表总体方差；n-1代表自由度

卡方分布
n个相互独立的随机变量，并服从标准（独立同分布于）正态分布。对每一个样本都计算它的卡方值那么这些卡方值将构成关于样本方差和总体方差的卡方分布。卡方分布是一个连续型概率分布，它的概率密度函数为：

代表卡方统计量；exp是自然底数，等于2.72；
·v代表自由度，等于样本容量n-1；
·c代表调节常数，使得卡方分布曲线下方的总面积等于1

 # 产生服从卡方分布的随机数
stats.chi2.rvs(df,loc=0,scale =1,size=1, random_state=None)

# 概率密度函数
stats.chi2.pdf pdf(x=随机变量,df=n[自由度],loc=0,scale =1,) 

# 累计分布函数：返回PDF在0到x上的积分，也就是概率分布函数的值
stats.chi2.cdf (x,df)

# 残存函数(1-cdf)
stats.chi2.sf 

 # 返回指定的统计数据（均值，方差，斜度，峰度）
stats.chi2.stats(df, ments='mvks')

# 数学期望
chi2.expect(func = f , args=(df,))

# 逆残存函数：返回值s满足chi2.cdf(s, n) = alpha， s就是alpha分位数
stats.chi2.isf (1-alpha, df)

# 返回值s满足chi2.cdf(s, n) = alpha， s就是alpha分位数
stats.chi2.ppf(alpha, df) 


stats.chi2.fit # 对随机取样进行你和，最大似然估计找到的概率密度函数系数

F分布

F分布处理的则是两个总体之间的关系，即通过两个样本之间的关系推导出两个总体之间的关系。
假设两个正态分布总体的方差分别为和，分别从两个正态分布总体中抽取样本容量为和的样本，样本方差分别为和，其F统计量为：

可以认为是两个卡方统计相除，也叫方差比分布，是方差分析的基础。其有俩个自由度，一般来说卡发值大的作为分母，小的作为分子，由分子和分母的两个自由度决定一个F分布曲线，F分布的概率密度函数为:

F：F统计量，：F统计量分子的自由度，：F统计量分母的自由度，c代表修正常数，它使得F分布曲线下方的总面积等于1。

因为F统计量是由两个独立的卡方统计量被各自的自由度相除后的
比，所以F分布的分布曲线与卡方分布曲线相似。随着自由度的增加，F分布的分布曲线也越来越对称，且对称的中点为1。