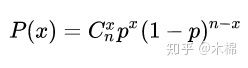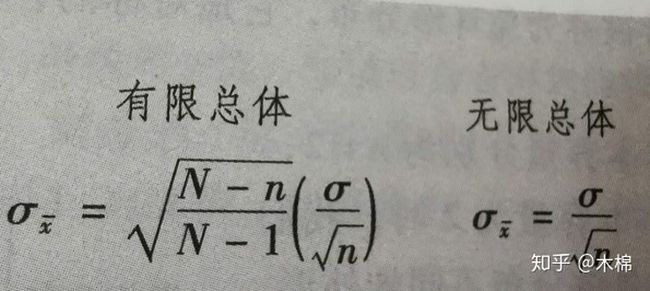根据概率分布随机采样python_统计概率思维及如何用python实现结果?
目录:
一、统计概率分布
二、如何用python实现概率分布?
三、总体和样本
一、统计概率分布
随机变量是对实验结果的数值描述。随机变量的值取决于实验结果,根据取值可以将概率分为离散型随机变量和连续型随机变量。
随机变量的概率分布式描述随机变量取不同值的概率。
引入三个常用的概念
期望:对随机变量中心位置的一种度量。
方差:度量随机变量取值的变异性或分散程度。
标准差:方差的算数平方根,其单位和随机变量的单位相同,描述一个随机变量的变异性。
概率分布有什么用?
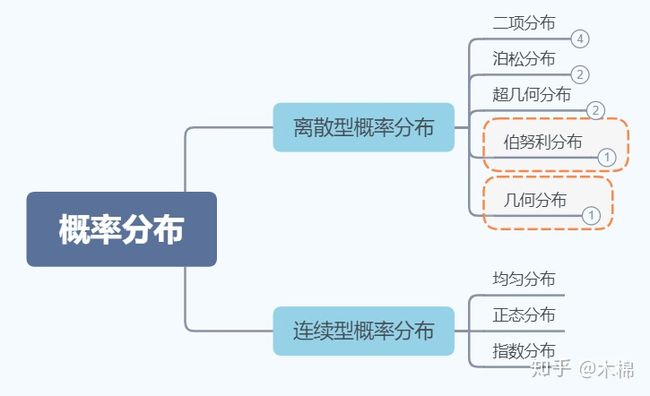
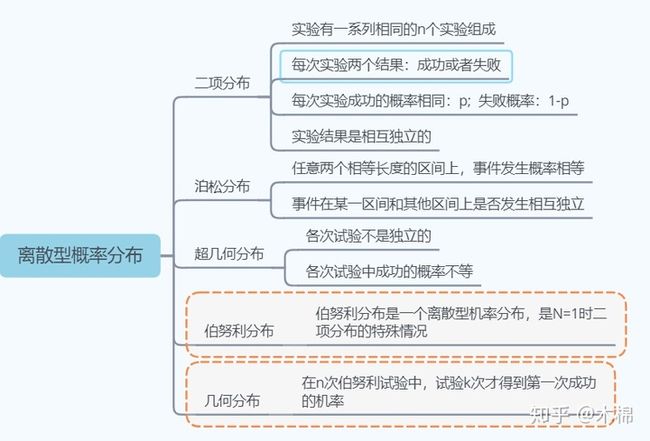
(1)离散型概率分布:
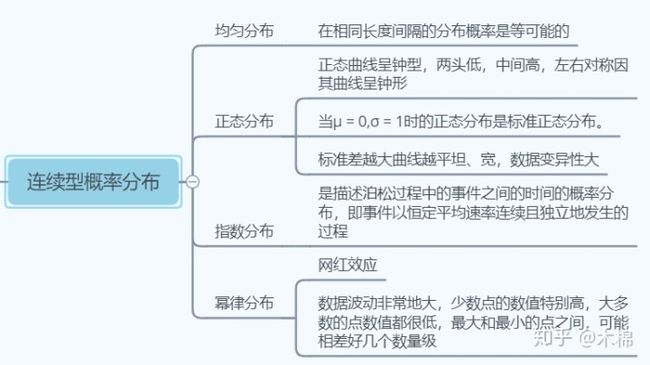
离散型概率分布(2)连续型概率分布:
补充:幂律分布无法用均值或方差等指标来反映度分布的聚合或者离散程度,所以,我们把它叫做“无标度”。
我们生活中各式各样的现象,从点击量、关注度、语言、城市人口,还有人脉、财富、声望,都遵循的是幂律分布。
幂律分布产生的原因是优先连接。新加入到网络中的节点,更倾向与超级节点产生连接。静态地看,你会看到不公平,但是,动态地看,你会看到新的机会仍然在不断涌现。
二、如何用python实现概率分布?
使用到的包有:numpy(n维数组),pandas(数据分析),matplotlib(绘图),scipy library(科学计算)。
导入科学计算包:
导入数组包和绘图包:
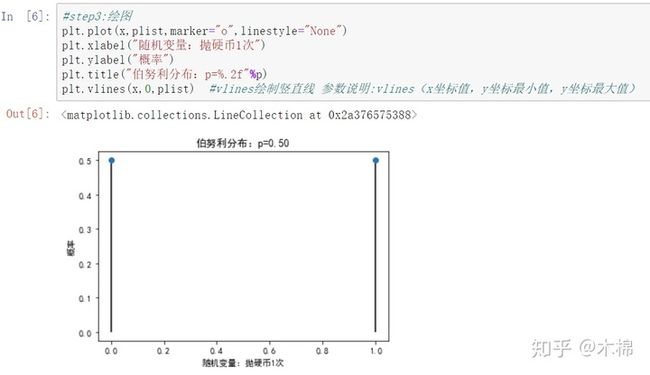
1、伯努利分布:stats.bernoulli.pmf(x,p)
定义随机变量,1次抛硬币,成功是指正面朝上记为1,失败是反面朝上记为0,
显示结果为一个列表,每个元素表示随机变量中对应值的概率。
绘图如下:
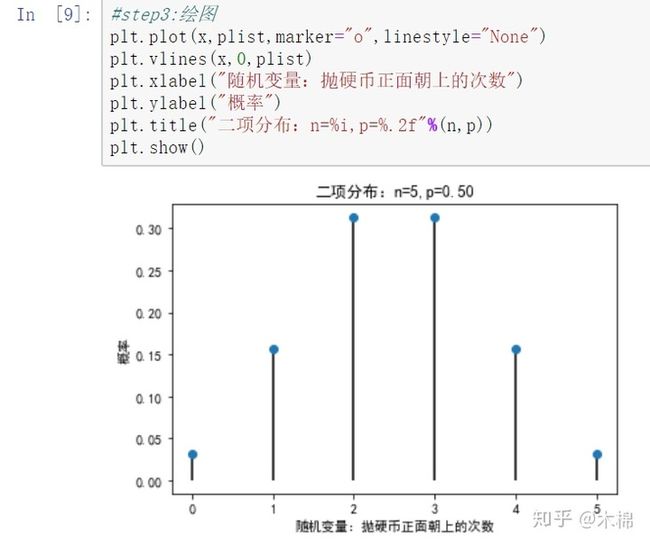
2、二项分布:plist=stats.binom.pmf(x,n,p)
(1)有什么用?
(2)如何检验?(符合概率分布的特性)
(3)如何计算概率?
(4)如何用python实现?(定义随机变量、计算概率、绘图)
举例:抛硬币
(1)有什么用?
想知道做某件事的概率有多大
(2)如何检验?
(3)如何计算概率?
(4)如何用python实现?
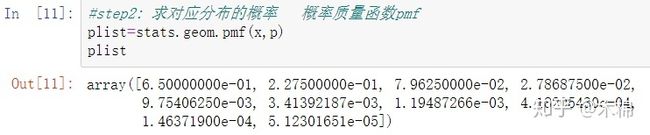
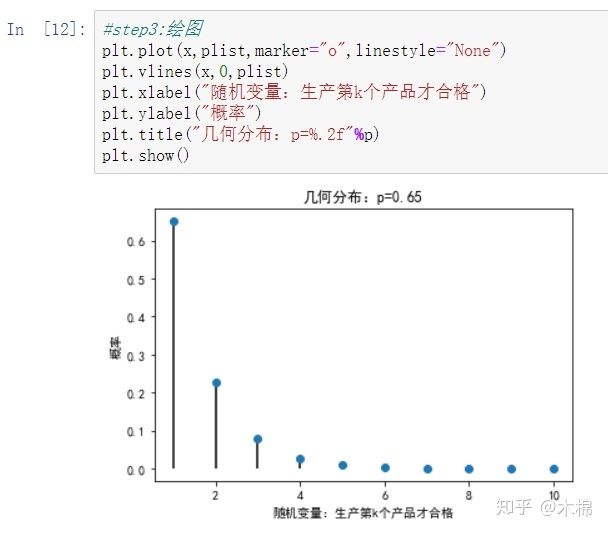
3、几何分布:stats.geom.pmf(x,p)
在伯努利试验中,记每次试验中事件A发生的概率为p,试验进行到事件A出现时停止,此时所进行的试验次数为X,其分布列为:
此分布列是几何数列的一般项,因此称X服从几何分布,记为X ~ GE(p) 。
实际中有不少随机变量服从几何分布,譬如,某产品的不合格率为0.05,则首次查到不合格品的检查次数X ~ GE(0.05)
几何分布的期望
方差
生成产品不合格案例:
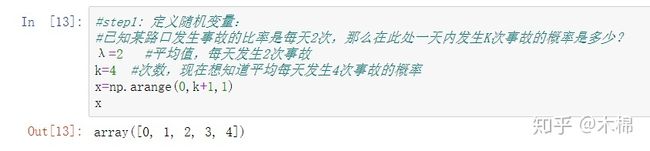
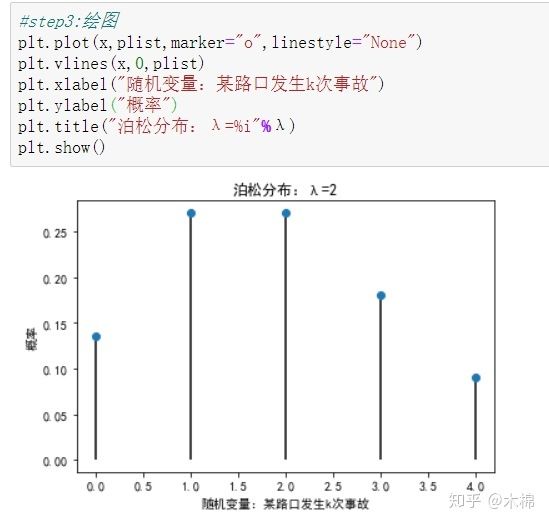
4、泊松分布:stats.poisson.pmf(x,λ)
泊松分布的概率函数为:
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为
特征函数为
交通事故案例:
5、正态分布:normal
一维正态分布:
标准正态分布:
多元正态分布在python的numpy库中有很方便一个函数:
np.random.multivariate_normal(mean=mean, cov=conv, size=N)
这个函数中,mean代表均值,是在每个维度中的均值。cov代表协方差矩阵,就像上面讲的那种形式,协方差矩阵值的大小将决定采样范围的大小。size代表需要采样生成的点数,此时输出大小为(N*D)的坐标矩阵
6、幂律分布:
假设变量x服从参数为
的幂律分布,则其概率密度函数可以表示为
如八二定律,80%的财富掌握在20%的人手里
如微博网红效应,大V拥有很多粉丝
三、总体和样本
1、总体:研究对象的整个群体
样本:从总体中选取的一部分,用于代表总体
样本大小(容量):每个样本里面有多少数据
抽样分布:将样本平均值的分布可视化
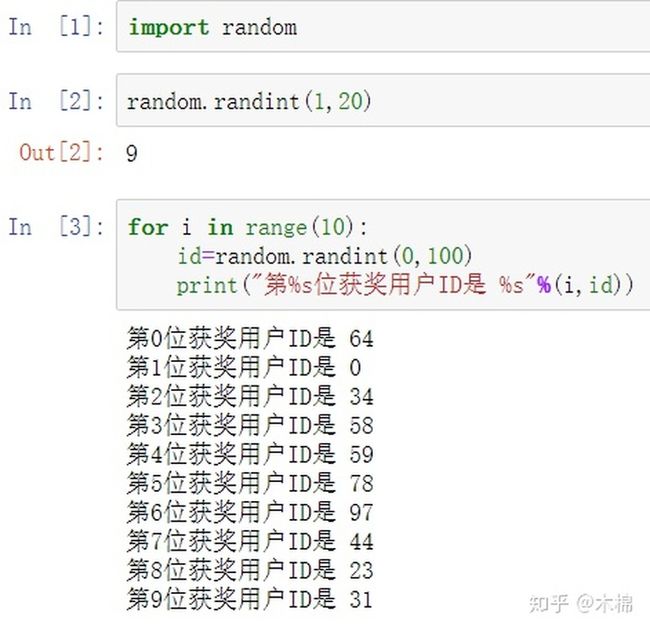
随机数random模块,用来生成随机数random.randint(a,b)
取值是包含a和b之间的数字
2、中心极限定理:
样本平均值约等于总体平均值
不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的平均值周围,并且呈现正态分布
3、如何用样本估算总体?
利用中心极限定理。
(1)利用样本平均值约等于总体平均值(中心极限定理)
(2)利用总体标准差估计。
抽样分布的均值等于总体均值,但是标准差和总体是否有限有关系:
n/N<=0.05时使用有限总体计算标准差,即左边第一个公式
n/N>0.05时接近1时使用无线总体计算标准差,即右边第二个公式
4、如何避免偏见?
(1)样本偏差:
在一般的统计或计量经济学研究中,用于估计所研究系统的参数的数据依赖于从总体中抽取的样本。如果所抽取的样本是随机的,即以类似“抽签”的方式获得的样本,根据这些样本数据所估计的各种参数能够准确反映总体的相关特性,理论上,就是所估计的参数是无偏的和一致的。而且随着抽取的样本越大,其对事件的总体特征分布的描述越是会准确。
常见的样本偏差有两种,一种是所抽取的样本不是随机的,另一种是抽取的样本数量不够多。
(2)幸存者偏差:
是一种常见的逻辑谬误。
逻辑谬误_百度百科baike.baidu.com指的是只能看到经过某种筛选而产生的结果,而没有意识到筛选的过程,因此忽略了被筛选掉的关键信息。日常表达为 “沉默的数据”、“死人不会说话”。
可以用对照试验和贝叶斯公式来消除幸存者偏差。
(3)概率偏见:
经济学家把人们自以为的概率称为心理概率,心理概率和客观概率不吻合,出现的偏差叫概率偏见。
出现有三个原因:代表性差(以偏概全)、可得性差(眼见为实)、沉锚效应(先入为主)
解决办法:学好数学,尤其是概率与统计;对没有办法验证客观概率的,也不要相信自己的直觉。
(4)信息茧房
指人们的信息领域会习惯性地被自己的兴趣所引导,从而将自己的生活桎梏于像蚕茧一般的“茧房”中的现象。
用以描述信息偏食所造成的风险。
例如个性化推荐,千人千面
这个概念在运用的过程中目前有利有弊。
,