multi-head attention之后的操作_从Transformer到Bert（一）： self-attention机制

通过标题Transformers变形金刚，大家应该可以猜到我们今天要讲变形金刚。 哦，no，其实是要讲一个非常流行的架构，叫做transformer。由于最近一年，Bert模型非常popular，大部分人都知道Bert，但是确不明白是什么，那么可能你需要先从tranformer了解清楚。

Transformer最先用于NLP的问题上，很多任务上实现了SOTA的表现，并且已经运用到很多其他领域。这个系列文章，就是想用最简单的方式来带大家了解transformer架构是如何工作的，如何从transformer演变到Bert的，而你，只需要一点大学基础的线性代数知识就可以。

在这里的第一篇，会着重介绍self-attention机制。（第二期请看这里）

---

Self-attention

Transformer架构最基础和最重要的操作就是self-attention.

Self-attention是一种sequence2sequence操作：通常将一个sequence转换成另外一个sequence。我们可以假设输入 vector是[x1,x2,...xt], 以及输出 vector是[y1,y2,...,yt]. 这里vector的维度都是k。

为了产生输出vector

, self-attention操作会对所有输入的vector进行加权平均

这里 j 是对整个sequence进行index（从1到t) 并且 weight的和在所有j上相加等于1（因为我们使用softmax，后面会提到）。这里的weight

不是我们通常学习机器学习里看到的参数，而是通过

和

的函数得到。最简单我们可以通过点乘法得到：

这样的点积可能会产生任意一个数，所以我们再采用softmax，把值投射到[0,1]的区间里，来保证在整个sequence上，他们的和为1.

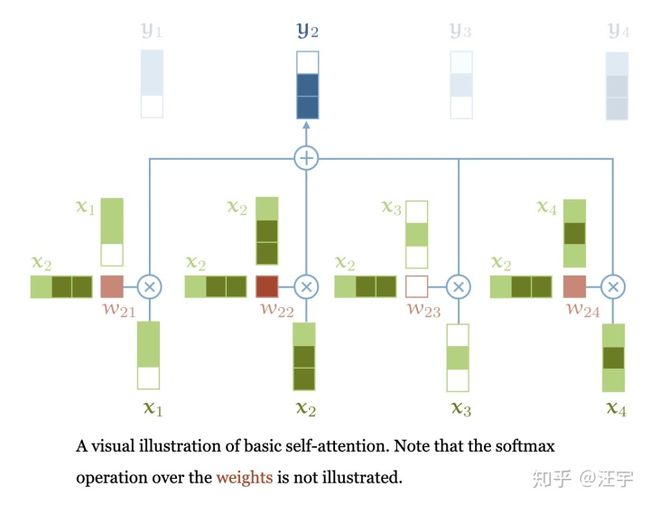
以上就是self attention的基本操作，下面附上一张图。

self-attention基本操作，这里softmax没有显示出来

还有一些其他成分来构成整个transformer，我们待会再说，但是self-attention是最基础的操作。更重要的是，这是整个transformer的架构里唯一保持vector之间信息流通的操作。所有其他的操作都是不在vector之间进行交互的。

掌握到这里，你已经掌握了精华的一部分，如果有兴趣，接着往下看：

理解为什么self-attention有效果

尽管上面的内容看起来很简单，但是为什么self-attention效果特别好，这一点并不是很容易理解。为了建立一些直观的理解，我们首先看看推荐系统中电影推荐一般的步骤。

假设你有一个电影网站，对于一些用户，你想推荐可能会喜欢的电影给他们。

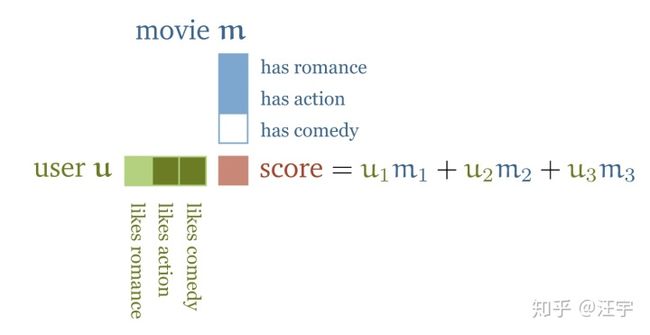
一种解决这类问题的方法是，先搜寻一些电影的特征值：比如这个电影的浪漫程度，动作片程度之类，然后设计相应的用户的特征：用户有多喜欢浪漫电影，有多喜欢动作片电影。如果这样做，两个vector（用户和电影）的点乘就会给你一个分数显示这个电影和用户的匹配程度，换句话说，就是用户可能喜欢这个电影的程度。

如果用户喜欢浪漫的电影，正好这个电影又是浪漫主题的，那么点乘score的结果就是正数positive，如果用户不喜欢浪漫电影，但是电影是浪漫主题，那么点乘的结果就是负数negative。

另外，这里的特征值本身的大小，也表明，他们自己对整体score的贡献是多大：一个电影可能很小一部分讲述动作武打，但并不是主要情节，或者用户本身只是轻微喜欢武打动作片，那么这一部分对于整个的结果影响就会比较小。

当然，或者这样的特征值本身实际情况下也许不太现实，或者很难获得，尤其是当你有上百万个电影的时候，标注起来就很困难，并且标注大量用户的喜欢和不喜欢也很困难。

取而代之的是，我们把电影的特征和用户的特征当做模型的参数，然后我们问用户他们喜欢的一些电影，然后我们根据这些来优化用户的特征和电影的特征使得他们的点乘值和这些已知的喜欢能够匹配。（知识点：这是大部分推荐系统的核心思想）

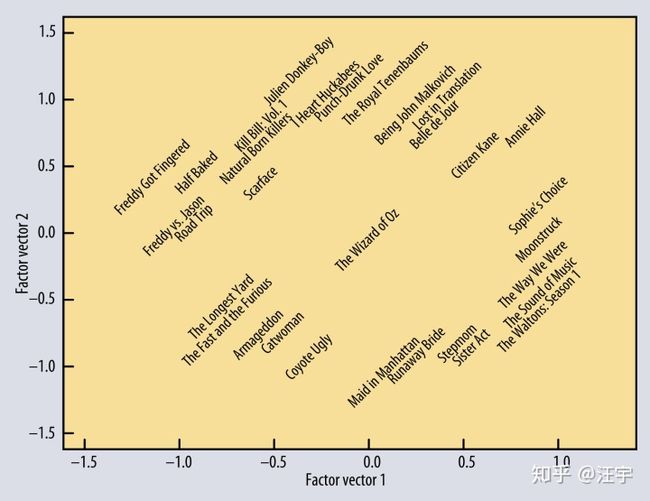
即使我们不能直接告诉模型每个特征值意味着什么，但在实际工程中，经过训练之后，特征值往往都能准确的反应电影内容的信息。很神奇是不是

这是从用户与电影之间的关系学习出来的电影特征的表达，投射在二维的空间里，完全没有用到电影内容信息。这表明仅仅通过这样的交互信息，实际上我们可以推测出电影本身的特征表达

这里的ppt可以帮助你理解更多关于推荐系统的基础知识。这里只是给大家解释点乘为什么能够帮我们来表达一个对象或者对象之间的关系。(这里的对象是object，不是lover :) ）

再回到self-attention,上面讲的就是self-attention的intuition。我们再回到sequence of words上。为了使用self-attention,我们给每个word t一个embedding vector，我们叫他

(有很多word embedding的技术，后面会稍微提一些）。这个通常在模型里叫做embedding层，它将每个word sequence：

the, cat, walks, on, the, street

投射成vector序列：

如果我们把这样的序列放进self-attention层，那么output就是另外一个vector序列：

这里

是对第一个sequence的所有embedding vectors的加权求和，权重分别是他们的和

点乘。

因为

也是我们训练出来的值，所以任意两个词之间有多接近，完全由这个训练任务决定的。在大多数情况下，‘

the' 的含义和其他单词的含义并没有非常有关联；因此，我们很可能得到一个embedding使得

和其他单词的embedding点积的绝对值比较小（不会影响最终结果）。从另一个方面来说，为了解释'

walk'在句中的含义，去找出是谁在walking就比较重要了。这有可能被一个名词（noun）表示，所以对于名词’ cat‘ 和动词’ walks‘, 我们就有可能会学到一个

和

使得他们的点积是一个比较大的正数。

这是self-attention背后的intuition。点积表达了两个vectors之间有多相关，’相关性‘是由具体任务定义的，输出vectors是输入sequence的加权求和，这里的权重取决于点乘的结果。

在我们往后面说之前，有几点值得注意，这些并不是普通的sequence2sequence模型里有的操作：

• self-attention把它的input认为是一个set，而不是一个sequence。如果我们变换整个input序列顺序，output的序列仍然会是一样。在真正做transformer的时候，我们会有一些改变，但是self-attention操作本身是忽略input的顺序的。
• 目前为止，我们还没有提到任何参数parameters。单纯self-attention是没有涉及任何参数的。当然在embedding layer是有参数需要学习，另外我们在后面还会添加一些parameters。（请接着往下看）

---

来用Pytorch实现一个self-attention

”所有我不能创造的，都不是真正理解“。 所以让我们一起来做一个简单的transformer。我们从建立基础的self-attention开始。如果你熟悉pytorch，或者不介意读一些代码，这一部分可以帮助你更深入理解，如果不是，也没有关系，直接跳过这一部分，随时都可以回过来看。

第一件事我们要做的就是如何用矩阵乘法表达self attention。一个简单的实现方法是对所有的vectors循环来计算权重，但是计算起来会特别慢。那么我们该怎么做？

我们来用一个t*k的矩阵 X 来表示一个长度为 t ，维度为 k 的vectors序列。再加上minibatch的维度/大小 b, 构成我们input tensor的维度是（b,t,k).

所有的点积结果

形成了一个矩阵，我们可以通过矩阵相乘 X 和

:

import 

然后，为了将

转变成postive的数值，并且和为1，我们需要采取 row-wise softmax（每一行进行softmax）：

weights = F.softmax(raw_weights, dim = 2)

最后，为了计算output sequence，我们只需要把weights和X相乘。最后我们的output矩阵 Y 的shape就是（b, t, k）

y = torch.bmm(weights, x)

Great，两个矩阵乘法和一个softmax，就给我们一个基础的self-attention的操作，并不是很复杂是不是。看到这你已经知道了一大半。

---

还有一些小诀窍

真正现代的transformer模型里用到的self-attention实际上还用到了三个小技巧：

1）Queries, keys and values

每个input vector

都在self attention里被用作三种不同的操作：

• query，用来和其他每个key vector进行交互，得到当前vector和其他vector的关联性，或者我们说的weights，用于计算自己的output
• key，用来和其他query vector进行交互, 帮助其他vector j 产生他的output
• value，将query和其他key产生得到的权重，跟自身的value进行加权求和，得到自己的output

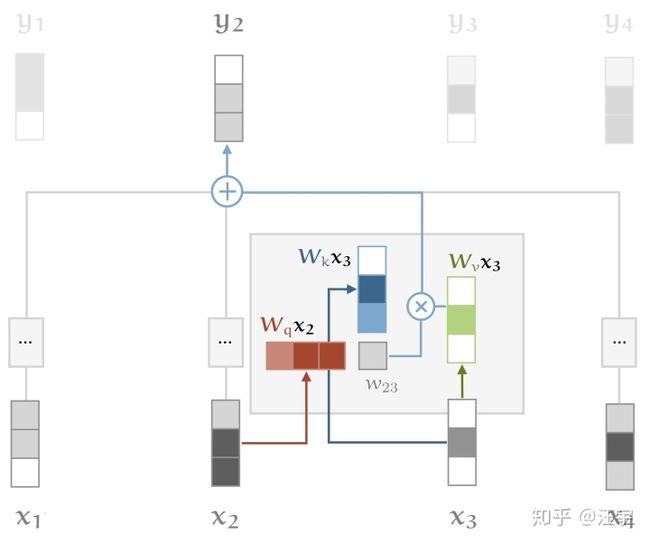
这就是我们说的query，key和value。在我们看到的基础的self-attention中，每个input vector都必须扮演者三个角色。为了让我们任务简单点，我们可以对input vector进行简单的线性转换，就可以得到这三个新的vectors。换句话说，我们添加三个 k*k的权重矩阵

,

,

然后计算三个线性转换：

,

,

这给了self-attention一些可以控制的参数，并且让它改变了input vectors使得他们能够扮演这三个角色。下面的图更能说明整个流程，self-attention以及key，query，value的变化。

2）调整点积的大小

softmax本身会对非常大的值很敏感，这会造成vanish gradient从而减缓训练速度，或者停止训练。因为点积的值会随着embedding dimension k的增大而增大，所以如果能按照dimension的大小，normalize一下，就可以防止softmax的结果变得太大：

也许你会问，为什么是

？你可以想象一个长为k 的vector，里面所有的值都是c，那么欧氏距离就为

。因此，我们为了防止这部分由维度增加导致的距离增大，需要除以

。

3）Multi-head attention

最后，我们需要考虑，一个单词可能在不同的语境下有不同的语义，看下面这个例子：

mary, gave, roses, to, susan

我们看到单词 gave 和句子中不同部分是有不一样的语义的意思。 ’mary' 表示who在giving， ‘roses'表明的what被given，’susan‘ 表明who是被given的人。 （突然化身英语老师）

在一个self-attention的操作里，所有的这些信息都加在一起。如果’susan'和’mary'换过来：‘susan gave roses to mary'，那么output

还是会相同，即使语义是不一样的。

我们可以给self-attention更多区分这样不同语义的能力，通过使用多个self attention（用r表示index），每个attention去关注不同的部分，我们称为attention heads.。每个权重用

,

,

。

对于input

，每个attention head都会产生不同的output

。我们把它们连接起来，一起通过一个线性的转换来把维度再降低为k。

---

用pytorch实现完整的self-attention

在又掌握一些诀窍之后，我们来实现一个完整的self-attention模块，我们把它包装到一个python的一个module里，这样可以复用。

import torch
from torch import nn
import torch.nn.functional as F

class SelfAttention(nn.Module):
    def __init__(self, k, heads = 8):
        super().__init__()
        self.k, self.heads = k, heads

我们可以用h个不一样的attention heads矩阵

,

,

来表示heads,但是更有效的方法是把所有的heads结合到三个k*hk的矩阵里，这样我们可以在一个大的矩阵里进行矩阵乘法运算。

        # input 维度为k（embedding结果），map成一个k*heads维度的矩阵
        self.tokeys    = nn.Linear(k, k * heads, bias = False)
        self.toqueries = nn.Linear(k, k * heads, bias = False)
        self.tovalues  = nn.Linear(k, k * heads, bias = False)
        # 在通过线性转换把维度压缩到 k
        self.unifyheads = nn.Linear(heads * k, k)

我们现在来实现self-attention的计算（通过forward 方法）。首先，我们计算queries, keys, values:

    def forward(self, x):
        b, t, k = x.size()
        h = self.heads

        queries = self.toqueries(x).view(b, t, h, k)
        keys    = self.tokeys(x).view(b, t, h, k)
        values  = self.tovalues(x).view(b, t, h, k)

每个Linear的输出都是（b, t, h*k）的维度,我们可以reshape到(b,t,h,k)的维度，这样可以给每个head他们自己的dimension。

下一步，我们需要计算点积（dot product)。这在每个head上的操作都是一样的，所以我们每次对一整个batch进行操作。这可以确保我们可以跟之前一样使用torch.bmm()，只是整个q,k,v的集合要更大一些，仅此而已。

因为head 和 batch的维度不是紧挨在一起，我们需要做矩阵的转置。（这看起来很费时间，但是不可避免）

        # 把 head 压缩进 batch的dimension
        queries = queries.transpose(1, 2).contiguous().view(b * h, t, k)
        keys    = keys.transpose(1, 2).contiguous().view(b * h, t, k)
        values  = values.transpose(1, 2).contiguous().view(b * h, t, k)

# 如果不明白contiguous()的意思，这篇博客讲的很清楚： https://zhuanlan.zhihu.com/p/64551412

跟之前一样，点积的结果可以被一个矩阵乘法搞定，只不过现在是queries和keys之间。

别忘了还要做一件事，就是把点积的结果需要normalize一下，除以

。其实更巧妙的做法是在queries和keys相乘前，normalize by

， 这可以对长的序列减少内存消耗：

        # 这等效于对点积进行normalize
        queries = queries / (k ** (1/4))
        keys = keys / (k ** (1/4))
        # 矩阵相乘
        dot  = torch.bmm(queries, keys.transpose(1,2))
        # 进行softmax归一化
        dot = F.softmax(dot, dim=2)

我们在把self attention采用到values 上，产生出最后每个head的output：

        out = torch.bmm(dot, values).view(b, h, t, k)

为了再把multi-head结合到一起，我们再转置一次，是的head的维度和embedding的维度贴到一起，然后reshape到合成的 k*h维度，再通过一个unifyheads 的线性转换，回归到k维。

        # swap h, t back, unify heads
        out = out.transpose(1, 2).contiguous().view(b, t, h*k)
        return self.unifyheads(out)

好啦，写到这，你就有了multi-head的self-attention了，这是transformer里最为关键的一部分了。

Transformer本身当然不只是self-attention这一层，想了解transformer的全貌？

看第二期：从Transformer到Bert（二）：构建transformer