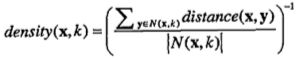2018异常检测综述——基于统计学、邻近度、密度、聚类的异常检测方法
目录
一、基础知识
异常成因
异常检测方法
异常检测的关键问题
二、基于统计学的方法
三、基于邻近度的方法
四、基于密度的方法
五、基于聚类的方法
异常检测(Anomaly Detection)也称偏差(deviation)检测或者离群点(outlier)检测,从数据的角度来看,其实就是检测出和众多其他观测值差别非常大的一个特殊的观测值。异常检测在历史上实际是数据预处理的一个步骤,但是在现代研究中越来越重要,逐渐发展为一个独立的领域。
我们要知道,自然界万物都可以被数学或数据描述。例如,图像,其实是可以用三通道矩阵来表达;模拟信号如电波等,可以转为离散化时间序列;我们的文字语言,也可以被“word2vec”,提取特征后用向量形式描述。所以,异常检测不仅仅只能用在数据领域,在不同的领域都可以发挥重要作用,它本质上就是检测离群的数据。
一、基础知识
异常成因
自然变异、数据测量和收集误差。
异常检测方法
基于模型的技术、基于邻近度的技术、基于密度的技术。
基于模型的技术首先建立一个数据模型,异常是那些模型不能完美拟合的对象。由于异常和正常对象可以看作定义两个不同的类,我们可以使用分类技术建立两个类的模型。但分类技术中训练集很重要,由于异常相对稀少,所以这样做通常比较难,需要加以考虑。
基于邻近度的技术考虑对象之间的邻近性度量,比如“距离”。基于密度的技术是认为低密度区域对象是异常点。
按照样本标签(正常、异常)可利用程度,可以分为:监督、半监督、无监督三种基本的异常检测方法。
有监督的异常检测:需要有异常类和正常类的训练集,分别为它们建立模型。但这会涉及到不平衡类问题,即异常样本总是相对稀少的。
半监督的异常检测:即从同时含有标注数据和未标注数据的训练集中学习模型。在监督学习中,因为训练集全部已经标记了,所以我们的兴趣点通常是在未来测试数据上的性能。而在半监督学习的分类问题中,训练数据中包含未标记的数据。因此,存在两个不同的目标。一个是预测测试集数据的类别,另一个是预测训练样本中未标记实例的类别(这里我们都假设是分类问题)。我们将前者称为inductive semi-supervised learning,将后者称为transductive learning。inductive semi-supervised learning就像考试,考试前你不知道有哪些问题(未来的测试数据),需要为所有的问题做准备(训练模型)。transductive learning就像做家庭作业,所有的问题都知道(训练样本中未标记的数据),你只要针对这些问题做准备(训练模型)。(参考一篇我认为归纳得不错的博文:半监督)
无监督异常检测:没有标签情况下,往往目标是将一个得分或标号赋予给每个数据对象。比如聚类算法,根据一些规则将数据进行无监督的聚类(没有提前训练模型,只是按照某些度量让相似数据聚集为一类)。简单直白地讲,如果聚类簇比较偏远,或者密度比较少,可能就是异常。
异常检测的关键问题
有一些关键的问题需要我们思考。
1、用于定义异常的属性个数。在异常检测中必须指明如何使用多个属性的值确定一个对象是否异常。数据维度很高时,这个问题尤其重要。
2、全局观点和局部观点。在之前讲优化算法的时候(《经验之谈:优化算法两句话精炼总结》),我们讲到优化算法无非解决2个问题:第一,搜寻全局最优;第二,解决局部最优。有时候有些数据在局部看似异常,但是在全局中可能很正常。这就需要我们的算法能够具备不同的视角。用黑话说,叫避免陷入局部最优。
3、某个数据对象的异常程度。某些技术直接赋予数据对象二元分类,即是异常或者不是异常。这样可能有些粗暴。如果我们的问题相对温和,可以考虑搞个离群点的得分(outlier score)来输出判别结果。
4、屏蔽和泥潭问题。一次识别一个异常的技术常常遇到屏蔽的问题,即如果有一场成群结对出现,可能会被无监督算法等视为正常的一簇点。一次检测多个异常的技术可能陷入泥潭,即把一堆正常的点判为利群点。
5、评估指标。由于异常类通常比正常类少得多,评估度量采取精度、召回率和假正率等度量可能更合适。
6、效率。各种异常检测方法的效率不同,要考虑到算法的开销或时间复杂度。比如如果基于统计方法建立了一个模型,用这个模型做预测,那可能只需要常数时间。如果基于邻近度的方法,时间复杂度通常为O(m^2)。
二、基于统计学的方法
统计方法是基于模型的方法。即先给数据们创建一个模型,根据对象拟合模型的情况来评估他们。大部分离群点检测方法总结起来无非就是:利用统计学方法建立一个模型,然后考虑对象有多大可能符合该模型。统计学上叫做考察不和谐的观测值(discordant observation)。
对于概率分布模型怎么搞出来,现在一般是通过估计参数的方法。即用户指定一些待估计的参数,比如高斯分布的μ和西格玛,然后用数据集的数据去估计它们,从而得到一个估计出来的模型。然后再进行下一步工作:比如检测一元正态分布中的离群点,用经典的3![]() 原则。多元正态分布中,就复杂一些,可能要用到基于协方差矩阵的Mahalanobis距离。
原则。多元正态分布中,就复杂一些,可能要用到基于协方差矩阵的Mahalanobis距离。
但是,如果选择了错误的模型,则对象很可能被错误地判为异常点。同时,大部分基于统计学的离群点检测技术都使用单个属性,多元数据(具有多个属性)应该如何建立其模型?这些都是目前面临的重要问题。
在基于统计学的方法中,一个有名的思路是使用混合分布。我们会另开一篇博文专门讲混合模型和EM算法。
如果有充分的数据和检验类型的先验知识,基于统计学的方法对单个属性的离群点检测可能非常有效。对于多元数据,可用的选择少一些;对于高维数据,检验的性能可能很差。
三、基于邻近度的方法
基于邻近度的方法思想很简单,就是一个对象如果原理大部分点,那就是异常。
这种方法比统计学更一般、更易用。因为确定数据集的有意义的邻近性度量比确定它的统计分布模型更容易。
基于邻近度的检测方案是简单的,但一般需要O(m^2)的时间,对于大型数据集可能代价过高。该方法也对参数敏感。此外,它不能处理具有不同密度区域的数据集,因为密度是局部特征,而距离是全局特征,它无法考虑到局部密度的变化。
四、基于密度的方法
在这个方法中,离群点是处于低密度区域中的对象。密度常用邻近度定义。
一个常用的定义密度的方法是:到K个最近邻的平均距离的倒数。该0距离小则密度高。
N是包含x的k-最近邻的集合,|N|是集合的大小。y是一个最近邻。
另一种密度定义是使用DBSCAN聚类算法使用的密度定义。
还有许多办法定义对象的相对密度。如x的密度是与它最近邻y的平均密度之比:
基于密度的方法也有一些局限性,大家可以自行思考一下。
五、基于聚类的方法
通过聚类可以创建数据的模型,而异常点的存在可以扭曲、破坏该模型。一个对象是基于聚类的离群点,如果该对象不强属于任何簇,或者说是丢弃、远离其他簇的小簇。
有些基于聚类的方法(如K均值)的时间和空间复杂度是线性或接近线性的,因而对离群点的检测可能高度有效。难点在于聚类簇个数的选择和异常点的存在性。不同簇个数下产生的结果或效果完全不一样。且粗的质量对所产生的离群点的质量影响非常大。每种聚类模型只适合特定的数据类型。
![]()