深度学习2：卷积神经网络Convolutional Neural Network（基于Python MXNet.Gluon框架）

卷积神经网络概述

  卷积神经网络是一种具有局部连接、权重共享等特性的深层前馈神经网络。

  目前的卷积神经网络一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络，使用反向传播算法进行训练。

  卷积神经网络有三个结构上的特性：局部连接、权重共享以及汇聚。这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性。和前馈神经网络相比，卷积神经网络的参数更少。

卷积 Convolution

一维卷积：一维卷积的概念来自信号处理中，用于计算信号的延迟累积。一个信号发生器每个时刻 产生一个信号 $x_t$，其信息的衰减率为 $w_k$，即在 $k-1$ 个时间步长后，信息为原来的 $w_k$ 倍。

  例如，假设 $w_1=1,w_2=\frac{1}{2},w_3=\frac{1}{4}$ ，那么在时刻 $t$ 收到的信号 $y_t$ 为前时刻产生的信息和以前时刻延迟信息的叠加

$$\begin{array}{rl}{y}_t=& w_1\cdot x_1+w_2\cdot x_2+w_3\cdot x_3\\ =& \sum _{k=1}^3{w}_k{x}_{t-k+1}.\end{array}$$

滤波器 Filter/卷积核 Convolution Kernel：$w_1,w_2,\cdots$称为滤波器。

  假设滤波器长度为 ，它和一个信号序列 $x_1,x_2,\cdots$ 的卷积为

$$y_t=\sum _{k=1}^K{w}_k{x}_{t-k+1}.$$

信号序列 和滤波器 的卷积定义为：

$$\text{y}=\text{w}\ast \text{x}.$$

一般情况下滤波器长度 $K$ 远小于信号序列长度 $N$。举一个一维卷积的例子：

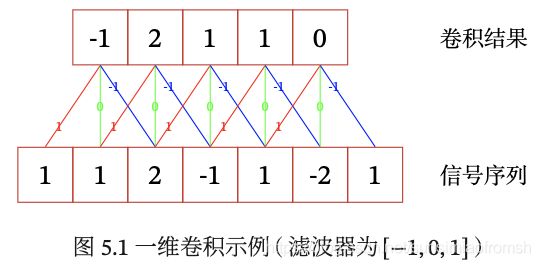
  滤波器为 $[-1,0,1]$，图中红线表示权重乘以1，绿线表示权重乘以0，蓝线表示权重乘以-1，恰好是滤波器倒过来的顺序。权重和输入相乘后相加得到一个结果，比如前三个输入 $[1,1,2]$ 和滤波器的卷积结果为 $1\cdot 1+1\cdot 0+2\cdot (-1)=-1$，同理可以得出其他几个卷积结果。

二维卷积：卷积也经常用在图像处理中。因为图像为一个二维结构，所以需要将一维卷积进行扩展。给定一个图像 $\text{X}\in {\mathbb{R}}^{M\times N}$和滤波器 $\text{W}\in {\mathbb{R}}^{U\times V}$，一般 $U$ 远小于 $M$，$V$ 远小于 $N$（对应一维情况下，滤波器长度 $K$ 远小于信号序列长度 $N$），其卷积为

$$y_{ij}=\sum _{u=1}^U\sum _{v=1}^V{w}_{uv}{x}_{i-u+1,j-v+1}$$

一个输入信息 $\text{X}$ 和滤波器 $\text{W}$ 的二维卷积定义为：

$$\text{Y}=\text{X}\ast \text{W}.$$

其中*表示二维卷积运算。举一个二维卷积的例子：

  输入信息为 $\left[\begin{array}{ccccc}1& 1& 1& 1& 1\\ -1& 0& -3& 0& 1\\ 2& 1& 1& -1& 0\\ 0& -1& 1& 2& 1\\ 1& 2& 1& 1& 1\end{array}\right]$，滤波器为 $\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& -1\end{array}\right]$，将滤波器矩阵翻转180度得到 $\left[\begin{array}{ccc}-1& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]$，然后从左到右、从上到下的与输入信息矩阵中的每一个三阶矩阵做元素加权和，得到二维卷积结果矩阵的值。

  以结果矩阵中第一行第一列的元素值为例，$0=1\cdot (-1)+1\cdot 0+1\cdot 0+(-1)\cdot 0+0\cdot 0+0\cdot 0+2\cdot 0+1\cdot 0+1\cdot 1$；再以结果矩阵中第一行第三列的元素值（计算方法如图赋权）为例，$-1=1\cdot (-1)+1\cdot 0+1\cdot 0+(-3)\cdot 0+0\cdot 0+1\cdot 0+1\cdot 0+(-1)\cdot 0+0\cdot 1$，同理可以得出其他几个卷积结果。

  下图蓝色矩阵是输入信息，绿色矩阵就是通过 $3\times 3$ 卷积核作用的结果，旁边的虚线多了一圈，即补零p=1.

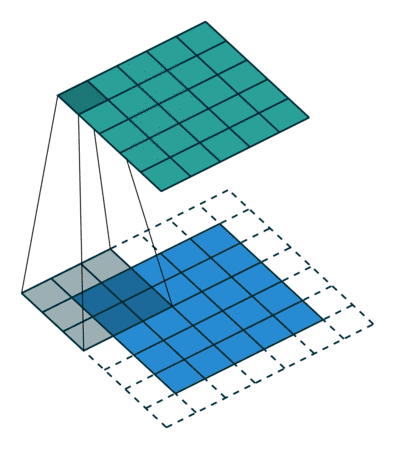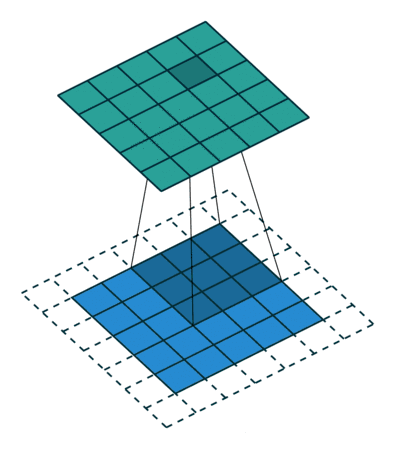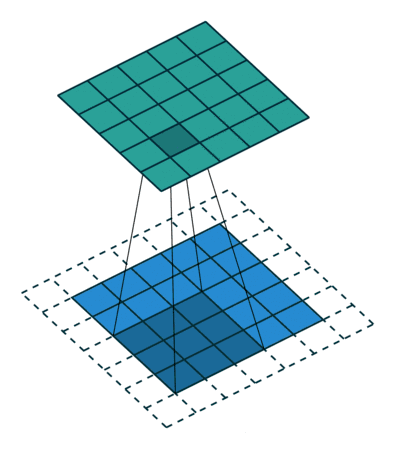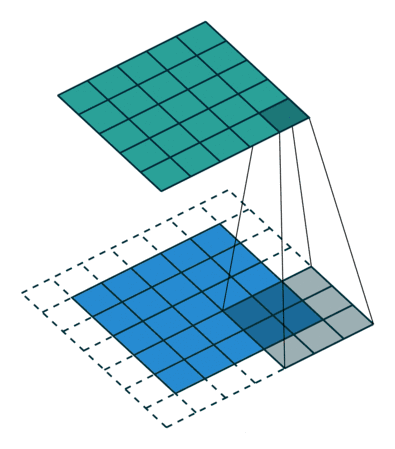
  在图像处理中，卷积经常作为特征提取的有效方法. 一幅图像在经过卷积操作后得到结果称为特征映射（Feature Map）。下图给出在图像处理中几种常用的滤波器，以及其对应的特征映射。图中最上面的滤波器是常用的高斯滤波器，可以用来对图像进行平滑去噪；中间和最下面的滤波器可以用来提取边缘特征。

互相关 Cross-Correlation

  在计算卷积的过程中，需要进行卷积核翻转。在具体实现上，一般会以互相关操作来代替卷积，（从上到下、从左到右）从而会减少一些不必要的操作或开销。

互相关：给定一个图像 $\text{X}\in {\mathbb{R}}^{M\times N}$和滤波器 $\text{W}\in {\mathbb{R}}^{U\times V}$，它们的互相关为

$$y_{ij}=\sum _{u=1}^U\sum _{v=1}^V{w}_{uv}{x}_{i+u-1,j+v-1}$$

  互相关和卷积的区别仅仅在于卷积核是否进行翻转。因此互相关也可以称为不翻转卷积。用公式表述即为：

$$\begin{array}{rl}Y=& \text{X}\otimes \text{W}\\ =& rot180(\text{X})\ast \text{W}\end{array}$$

  在神经网络中使用卷积是为了进行特征抽取，卷积核是否进行翻转和其特征抽取的能力无关。特别是当卷积核是可学习的参数时，卷积和互相关在能力上是等价的。因此，为了实现上（或描述上）的方便起见，我们用互相关来代替卷积。事实上，很多深度学习工具中卷积操作其实都是互相关操作。

卷积的类别

滤波器的步长 Stride：是指滤波器在滑动时的时间间隔。

零填充 Zero Padding：是在输入向量两端进行补零。

  对两个概念的举例如下：

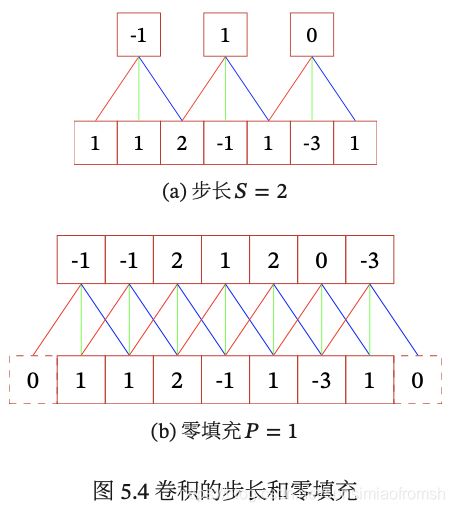
  一般常用的卷积有以下三类：

  假设卷积层的输入神经元个数为 ，卷积大小为 ，步长为 ，在输入两端各填补 个 0，那么该卷积层的神经元数量为$\frac{M-K+2P}{S+1}$.

窄卷积 Narrow Convolution：步长 = 1，两端不补零 = 0，卷积后输出长度为 − + 1.

宽卷积 Wide Convolution：步长 = 1，两端补零 = − 1，卷积后输 出长度 + − 1.

等宽卷积 Equal-Width Convolution：步长 = 1，两端补零 = ( − 1) / 2，卷积后输出长度 .

  上图b就是一个等宽卷积示例。

卷积神经网络

用卷积来代替全连接

  在全连接前馈神经网络中，如果第 层有 $M_l$ 个神经元，第 − 1 层有 $M_{l-1}$ 个 神经元，连接边有 $M_l\times M_{l-1}$ 个，也就是权重矩阵有 $M_l\times M_{l-1}$ 个参数。当 $M_l$ 和 $M_{l-1}$ 都很大时，权重矩阵的参数非常多，训练的效率会非常低。

  如果采用卷积来代替全连接，第 层的净输入 $z^{(l)}$ 为第 − 1 层活性值 $a^{(l-1)}$ 和滤波器 $w^{(l)}\in {\mathbb{R}}^K$ 的卷积，即

$$z^{(l)}=w^{(l)}\otimes a^{(l-1)}+b^{(l)},$$

其中滤波器 $w^{(l)}\in {\mathbb{R}}^K$ 为可学习的权重向量，$b^{(l)}\in \mathbb{R}$ 为可学习的偏置。

  卷积层有两个很重要的性质:

局部连接：在卷积层（假设是第 $l$ 层）中的每一个神经元都只和下一层（第 $l-1$ 层）中某个局部窗口内的神经元相连，构成一个局部连接网络。如图所示，卷积层和下一层之间的连接数大大减少，由原来的 $M_l\times M_{l-1}$ 个连接变为 $M_l\times K$ 个连接， 为滤波器大小。

权重共享：从公式$z^{(l)}=w^{(l)}\otimes a^{(l-1)}+b^{(l)}$可以看出，作为参数的滤波器 $w^{(l)}$ 对于第 $l$ 层的所有的神经元都是相同的。如图，所有的同颜色连接上的权重是相同的。权重共享可以理解为一个滤波器只捕捉输入数据中的一种特定的局部特征。因此，如果要提取多种特征就需要使用多个不同的滤波器。

  由于局部连接和权重共享，卷积层的参数只有一个 维的权重 $w^{(l)}$ 和 1 维的偏置 $b^{(l)}$ ，共 + 1 个参数。参数个数和神经元的数量无关。此外，第 层的神经元个数不是任意选择的，而是满足 $M_l=M_{l-1}-K+1$.

卷积层

特征映射 Feature Map：为一幅图像（或其他特征映射）在经过卷积提取到的特征，每个特征映射可以作为一类抽取的图像特征。为了提高卷积网络的表示能力，可以在每一层使用多个不同的特征映射，以更好地表示图像的特征。

  在输入层，特征映射就是图像本身。如果是灰度图像，就是有一个特征映射， 输入层的深度 = 1；如果是彩色图像，分别有 RGB 三个颜色通道的特征映射，输入层的深度 = 3。

  不失一般性，假设一个卷积层的结构如下：

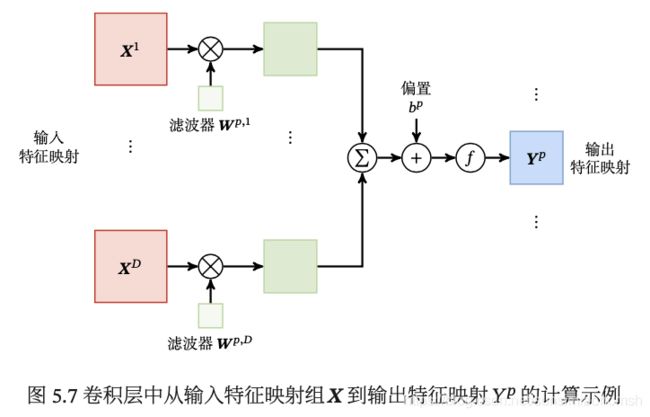
1. 输入特征映射组：$X\in {\mathbb{R}}^{M\times N\times D}$ 为三维张量（Tensor），其中每个切片（Slice）矩阵 ${\text{X}}^d\in {\mathbb{R}}^{M\times N}$ 为一个输入特征映射，1 ≤ ≤ ；
2. 输出特征映射组：$Y\in {\mathbb{R}}^{M^{\prime }\times N^{\prime }\times P}$ 为三维张量，其中每个切片矩阵 ${\text{Y}}^p\in {\mathbb{R}}^{M^{\prime }\times N^{\prime }}$ 为一个输出特征映射，1 ≤ ≤ ；
3. 卷积核：$W\in {\mathbb{R}}^{U\times V\times D\times P}$ 为四维张量，其中每个切片矩阵 ${\text{W}}^{p,d}\in {\mathbb{R}}^{U\times V}$ 为一个二维卷积核，1 ≤ ≤ ，1 ≤ ≤ .

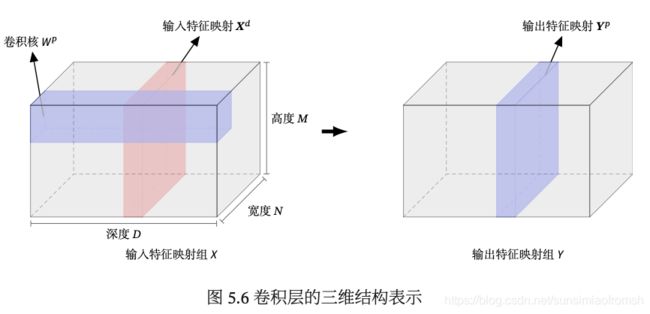
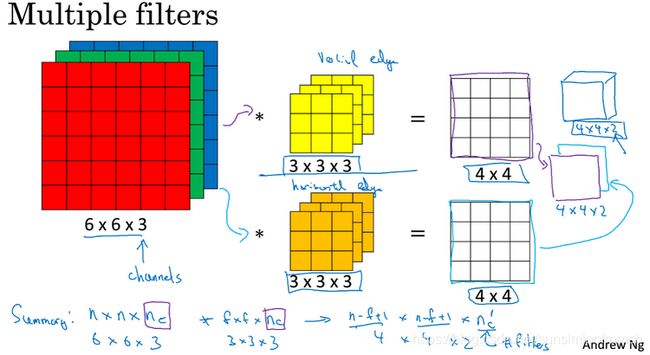
  利用下图解释M，N，M’，N’，U，V，P，D：

1. 输入层：M=6，N=6，D=3；
2. 输出层：M’=4，N’=4，P=2；输入层信息通过2个 $3\times 3\times 3$ 的卷积核，卷积后产生2个 $4\times 4$ 的结果；
3. 卷积核：U=3，V=3，D=3，P=2；2个 $3\times 3\times 3$ 的卷积核.

  在深度学习的算法学习中，都会提到 channels 这个概念。根据CSDN博主：scxyz_的总结，偏好把 channels 分为三种¹：

1. 最初输入的图片样本的 channels ，取决于图片类型，比如RGB，channels=3；
2. 卷积操作完成后输出的 out_channels ，取决于卷积核的数量。此时的 out_channels 也会作为下一次卷积时的卷积核的 in_channels；
3. 卷积核中的 in_channels ，2. 中已经说了，就是上一次卷积的 out_channels ，如果是第一次做卷积，就是1. 中样本图片的 channels 。

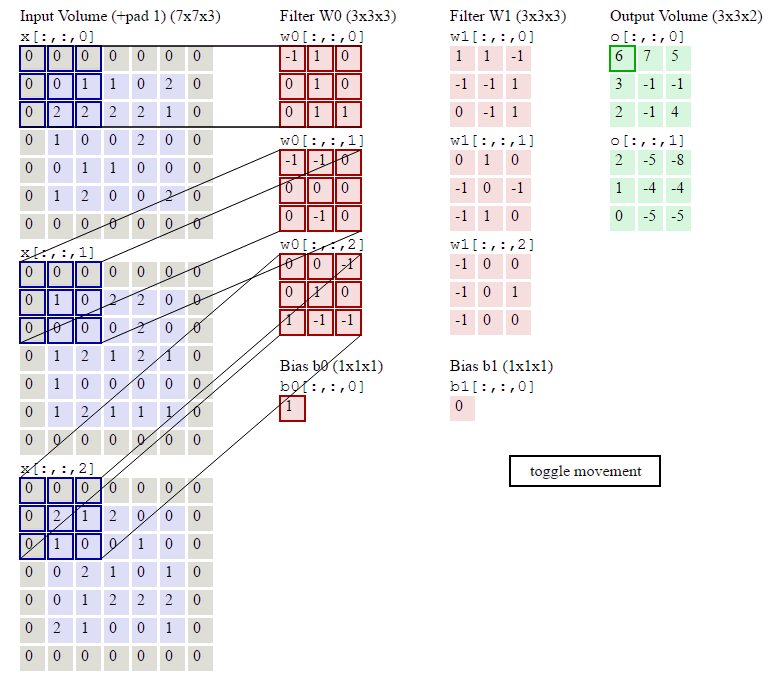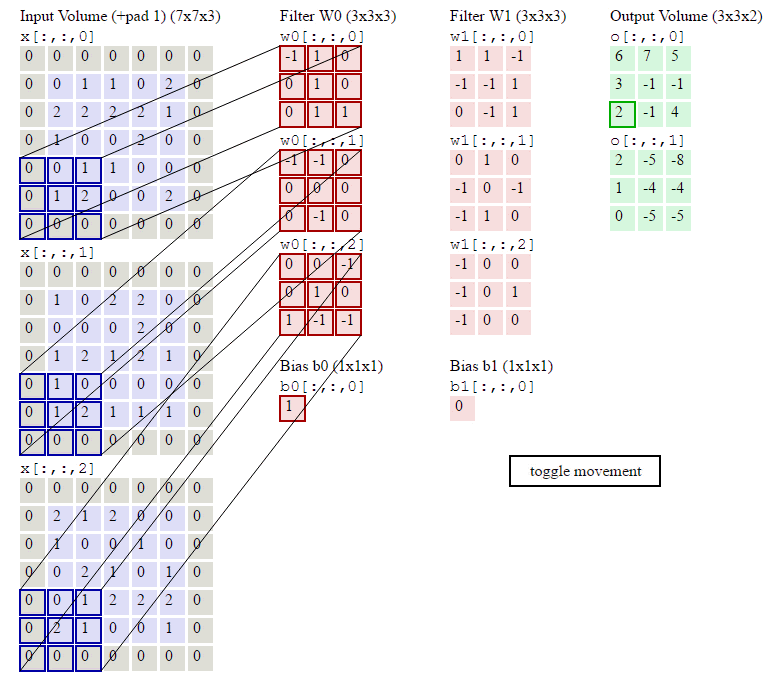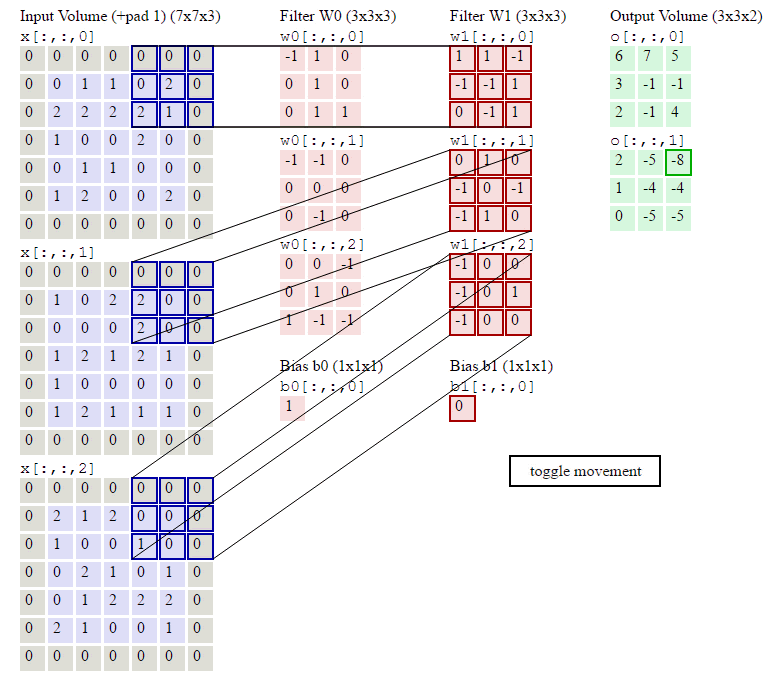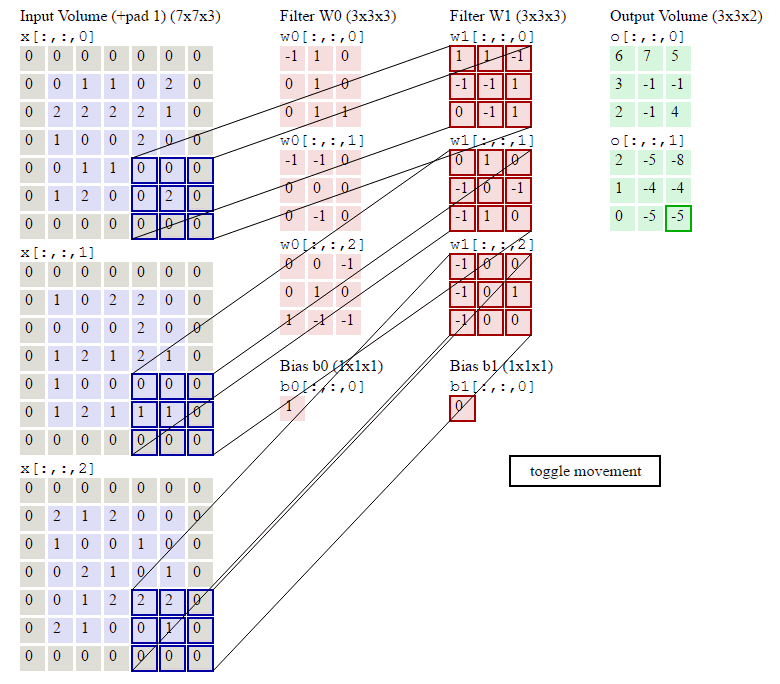
下图是一个多通道多滤波器的实例：

汇聚层/池化层

汇聚层 Pooling Layer：也叫子采样层（Subsampling Layer），其作用是进行特征选择，降低特征数量，从而减少参数数量。

  卷积层虽然可以显著减少网络中连接的数量，但特征映射组中的神经元个数并没有显著减少。如果后面接一个分类器，分类器的输入维数依然很高，很容易出现过拟合。为了解决这个问题，可以在卷积层之后加上一个汇聚层，从而降低特征维数，避免过拟合。

  常用的汇聚函数有两种：

1. 最大汇聚 Max Pooling：对于一个区域 $R_{m,n}^d$，选择这个区域内所有神经元的最大活性值作为这个区域的表示。
   $$y_{m,n}^d=ma{x}_{i\in R_{m,n}^d}{x}_i，$$
   其中 $x_i$ 为区域 $R_{m,n}^d$ 内每个神经元的活性值。
2. 平均汇聚 Mean Pooling：一般是取区域内所有神经元活性值的平均值。
   $$y_{m,n}^d=\frac{1}{|R_{m,n}^d|}\sum _{i\in R_{m,n}^d}{x}_i.$$

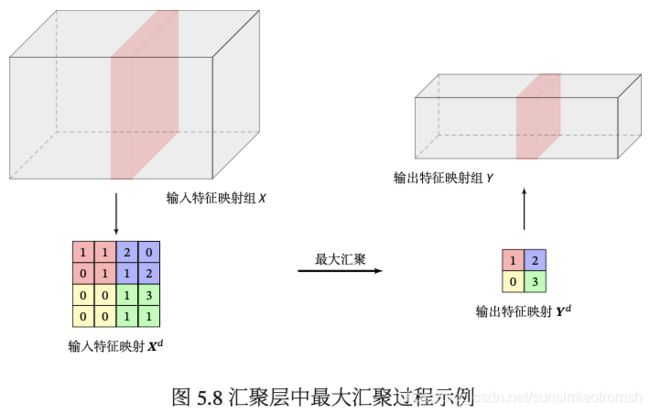
  目前主流的卷积网络中，汇聚层仅包含下采样操作。但在早期的一些卷积网络(比如 LeNet-5)中，有时也会在汇聚层使用非线性激活函数。

  典型的汇聚层是将每个特征映射划分为 2 × 2 大小的不重叠区域，然后使用最大汇聚的方式进行下采样。

  汇聚层也可以看作是一个特殊的卷积层，卷积核大小为 × ，步长为 × ，卷积核为 max 函数或 mean 函数。过大的采样区域会急剧减少神经元的数量，也会造成过多的信息损失。

  一个典型的卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成。目前常用的卷积网络结构如图所示。一个卷积块为连续 个卷积层和 个汇聚层（ 通常设置为 2 ∼ 5， 为 0 或 1）。一个卷积网络中可以堆叠 个连续的卷积块， 然后在后面接着 个全连接层（ 的取值区间比较大，比如 1 ∼ 100 或者更大； 一般为0～2）。

  目前，整个网络结构趋向于使用更小的卷积核（比如 1 × 1 和 3 × 3）以及更深的结构（比如层数大于50）。此外，由于卷积的操作性越来越灵活（比如不同的步长），汇聚层的作用也变得越来越小，因此目前比较流行的卷积网络中，汇聚层的比例正在逐渐降低，趋向于全卷积网络。

参数学习

  在卷积网络中，参数为卷积核中权重以及偏置。和全连接前馈网络类似，卷积网络也可以通过误差反向传播算法来进行参数学习。

  在卷积神经网络中，主要有两种不同功能的神经层：卷积层和汇聚层。而参数为卷积核以及偏置，因此只需要计算卷积层中参数的梯度。

卷积的数学性质

误差项的计算

几种典型的卷积神经网络

LeNet-5

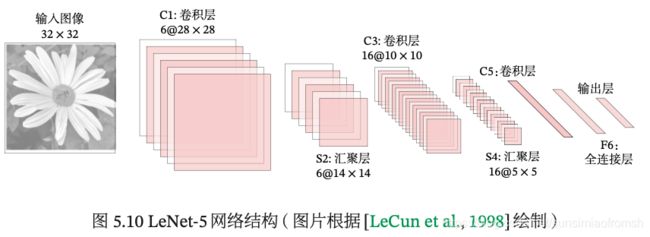
  LeNet-5 共有 7 层，接受输入图像大小为 32 × 32 = 1 024，输出对应 10 个类别的得分。LeNet-5 中的每一层结构如下（其中的理解²参考了CSDN博主：saw009的文章，saw009博主️灰常666666）：

1. C1层是卷积层：
   滤波器：6个5 × 5的滤波器；
   补零数：p=0；
   步长：s=1；
   特征映射结果：6 组大小为28 × 28 = 784的特征映射；
   C1 层的神经元数量：6 × 28 × 28 = 4 704个神经元；
   可训练参数数量：6 × 25 + 6 = 156个可训练参数；
   解释：由于局部连接和权重共享，卷积层C1每个特征映射对应5 × 5 = 25个权重（即对输入的单通道信息使用的滤波器有5 × 5 = 25个元素）和1个偏置，从而6个特征映射就有 6 × 25 + 6 = 156个参数。
   连接数：6 × (25 + 1) × 784 = 122 304个连接数（包括偏置在内，下同）。
   解释：即可训练参数数量 × 卷积层C1其中一个特征映射的神经元个数，每个特征映射中的每个神经元都有 25 + 1 = 26个参数连接，则每个特征映射都有 (25 + 1) × 784个连接，从而6个特征映射就有 6 × (25 + 1) × 784 = 122 304个连接。

2. S2 层为汇聚层
   采样窗口大小：大小为2 × 2；
   补零数：p=0；
   步长：s=2；
   汇聚函数：平均汇聚函数；
   是否使用激活函数：是，使用一个非线性激活函数，形如 ${\text{Y}}^{{}^{\prime }d}=f(w^d{\text{Y}}^d+b^d)$；
   S2 层的神经元个数：6 × 14 × 14 = 1 176个神经元；
   解释：在卷积层C1的每个 28 × 28 映射中，用 2 × 2 的窗口不带交集的平移过去，可以得到 14 × 14 个这样的采样窗口，取每个窗口内的元素的平均值作为汇聚层S2中的一个元素，得到汇聚层S2中的一个通道，含为 14 × 14 个神经元，从而6个通道共有 6 × 14 × 14 = 1 176个神经元。
   
   可训练参数数量：6 × (1 + 1) = 12个可训练参数；
   解释：其中第一个"1"为汇聚层中2 × 2 采样窗口中平均数对应的权重，第二个"1"为偏置，这个汇聚层有权重和偏置，是因为LeNet-5在汇聚层使用非线性激活函数 $${\text{Y}}^{{}^{\prime }d}=f(w^d{\text{Y}}^d+b^d)$$一般情况的汇聚层只包含下采样操作，不具备权重和偏置。
   连接数：6 × (14 × 14) × (4+1) = 5880个连接数（包括偏置在内，下同）。
   解释：虽然只选取 2 × 2 采样窗口中的平均数，但也存在 2 × 2 的连接数，即将 2 × 2 采样窗口内每个数的权重看作 1/4（不可训练，与前面那个可训练参数w不一样）。汇聚层S2的每个神经元，都是由上一层的一个采样窗口求平均得到的，因此对应了 4 个权重连接，还有1个偏置连接，因此汇聚层S2的每个通道有 14 × 14 × (4+1) 的连接，从而6个通道共有 6 × 14 × 14 × (4+1) = 5880个连接。
   若使用最大汇聚，虽然只选取 2 × 2 感受野中最大的那个数，但也存在 2 × 2 + 1 的连接数，即最大那个数的权重为1，其余数的权重为0，还有一个偏置的连接。

3. C3 层为卷积层
   滤波器：LeNet-5 中用一个连接表来定义输入和输出特征映射之间的依赖关系，如下图所示，共使用 60 个 5 × 5 的滤波器；
   
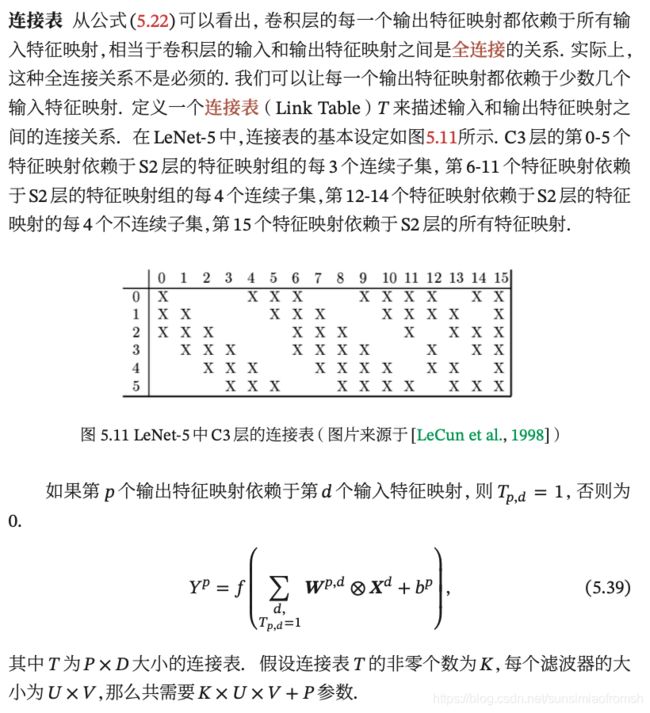
   该层第一个难点：6个输入如何通过卷积得到16个特征映射？
   
   如图2所示，卷积层C3的前六个特征映射(0,1,2,3,4,5)由汇聚层S2的相邻三个特征映射作为输入，接下来的6个特征映射(6,7,8,9,10,11)由S2的相邻四个特征映射作为输入，12,13,14号特征映射由S2间断的四个特征映射作为输入，15号特征映射由S2全部(6个)特征映射作为输入。
   该层第二个难点：通过S2的输入，如何卷积得到C3的一个特征映射呢？
   
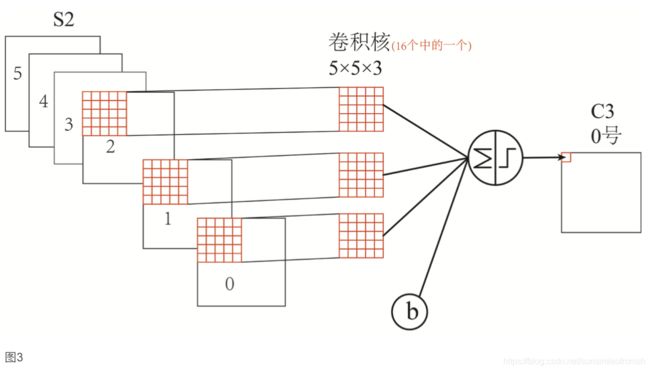
   以卷积层C3的0号特征映射举例（如图3所示）3个 5 × 5 的滤波器以步长=1，补零=0和汇聚层S2的0,1,2号输出映射进行卷积，求和，得到卷积层C3的0号特征映射。
   解释：根据第一个难点的解释可知，得到卷积层C3的前六个特征映射(0,1,2,3,4,5)由汇聚层S2的相邻三个特征映射作为输入，每个输入动用了3个滤波器，从而C3的前六个特征映射共动用了6 × 3 =18个滤波器；同理C3的接下来六个特征映射共动用了6 × 4 =24个滤波器，再接下来四个特征映射共动用了3 × 4 =12个滤波器，最后一个特征映射共动用了1 × 6 =6个滤波器，所以共计18 + 24 + 12 + 6 = 60个滤波器。
   特征映射结果：得到 16 组大小为 10 × 10 的特征映射；
   解释：根据连接图可知，得到了16个特征映射。根据图3，由于每个特征映射都是3个汇聚层S2中大小为 14 × 14 的特征映射，经过3通道卷积核 5 × 5 卷积得来的，因此输出结果每个通道大小为 (14 - 5 + 1) × (14 - 5 + 1) = 10 × 10，从而输出卷积层C3的结果为16 组大小为 10 × 10 的特征映射。
   C3 层的神经元数量：16 × 100 = 1 600个神经元；
   可训练参数数量：（5 × 5 × 3+1）× 6+（5 × 5 × 4+1）× 6+（5 × 5 × 4+1）× 3+（5 × 5 × 6+1）× 1 = 1516个可训练参数；
   连接数：1 516 × 100 = 151 600个连接数。
   解释：可训练参数数量 × 卷积层C1其中一个特征映射的神经元个数。

4. S4 层是一个汇聚层
   采样窗口大小： 2 × 2；
   补零数：p=0；
   步长：s=2；
   特征映射结果：得到 16 个 5 × 5 大小的特征映射；
   S4 层的神经元数量：16 × 5 × 5 = 400个神经元；
   可训练参数数量： 16 × 2 = 32个可训练参数；
   连接数： 16 × (5 × 5) × (4 + 1) = 2 000个连接数。

5. C5层是一个卷积层
   滤波器：使用120 × 16 = 1920个5 × 5的滤波器；
   补零数：p=0；
   步长：s=1；
   特征映射结果：得到120组大小为 1 × 1 的特征映射；
   C5 层的神经元数量：120 × 1 × 1 = 120个神经元；
   可训练参数数量：120 × 16 × 25 + 120 = 48 120个可训练参数；
   解释：卷积层C5的每个特征映射对应有16 × 5 × 5 = 400个权重（即对应16通道的汇聚层C5，所使用的每16个滤波器共16 × 5 × 5 = 400个元素）和1个偏置，从而120个特征映射就有120 × 16 × 25 + 120 = 48 120个参数。
   连接数：120 × (16 × 25 + 1) = 48 120个连接数。
   解释：卷积层C5中每个特征映射对应了 16 × 25个权重和1个偏置，从而共有 120 × (16 × 25 + 1) = 48 120个连接数。

6. F6 层是一个全连接层
   F6 层的神经元数量： 84 个神经元（之所以选这个数字的原因来自于输出层的设计）；
   可训练参数数量：84 × (120 + 1) = 10 164；
   连接数：和可训练参数个数相同，为 10 164。

7. 输出层，输出层由 10 个径向基函数(Radial Basis Function，RBF)组成。

AlexNet

  AlexNet是第一个现代深度卷积网络模型，其首次使用了很多现代深度卷积网络的技术方法，比如使用 GPU 进行并行训练，采用了 ReLU 作为非线性激活函数，使用 Dropout 防止过拟合，使用数据增强来提高模型准确率等。

  AlexNet 的结构如图所示，包括 5 个卷积层、3 个汇聚层和 3 个全连接层（其中最后一层是使用Softmax函数的输出层）。因为网络规模超出了当时的单个 GPU 的内存限制，AlexNet 将网络拆为两半，分别放在两个 GPU 上，GPU 间只在某些层(比如第 3 层)进行通信。

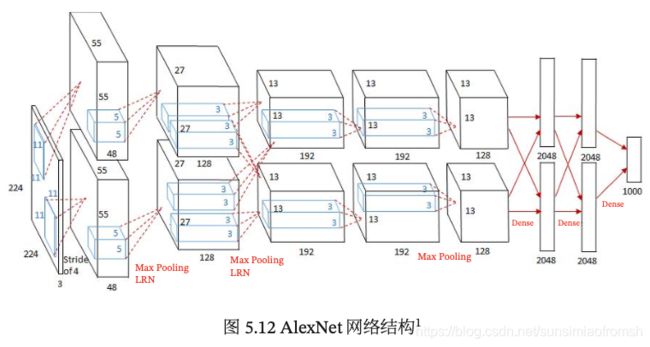
   AlexNet 的输入为 224 × 224 × 3 的图像，输出为 1 000 个类别的条件概率，具体结构如下：

提示1：对于宽和高都相等（都为H）的二维输入，使用高和宽相等（都为K）、步长为S、零填充为P的卷积层或汇聚层，则会产生高和宽都相等的二维输出，大小为[$\frac{H-K+2P+S}{S}$]（[取整符号]）。

提示2：卷积层的参数 = 卷积核大小 x 卷积核的数量
+偏置数量(即卷积的核数量)³。

提示3：全连接层的参数数量 = 上一层节点数量 x 下一层节点数量 + 偏置数量（即下一层的节点数量)³。

1. 第一个卷积层
   滤波器：使用 2 个大小为 11 × 11 × 3 × 48 的卷积核；
   解释：对于每一个通道（即每个GPU上），使用 48 个 11 × 11 × 3 的滤波器，其中 3 是深度。
   步长： = 4；
   零填充： = 3；
   特征映射结果：得到 2 个大小为 55 × 55 × 48 的特征映射组；
   解释：对于每一个通道，经过滤波器卷积后，得到深度为 48 的一个映射特征。这里H=224，K=11，S=4，P=3，则每个映射特征大小（宽 × 高）为 55 × 55，从而每个通道的映射特征大小为 55 × 55 × 48。
   可训练参数数量：(11 × 11 × 3 + 1) × 48 × 2个可训练参数。
   解释：对于每个通道的每个深度，都是由一个 11 × 11 × 3 的卷积核卷积而来，因此每个深度有 11 × 11 × 3 个权重，除此之外每个深度还对应 1 个偏置，从而共有 11 × 11 × 3 + 1个可训练参数，那么 2 个通道、每个通道 48 个深度共有 (11 × 11 × 3 + 1) × 48 × 2 个可训练参数。

2. 第一个汇聚层
   采样窗口及汇聚函数：使用大小为 3 × 3 的最大汇聚操作；
   步长：步长 = 2；
   特征映射结果：得到 2 个 27 × 27 × 48 的特征映射组。
   解释：对于每一个通道，经过 3 × 3 的最大汇聚操作后，得到深度仍为 48 的一个映射特征（汇聚层并不会改变特征映射深度）。这里H=55，K=3，S=2，P=0，则每个映射特征大小（宽 × 高）为 27 × 27，从而每个通道的映射特征大小为 27 × 27 × 48。
   可训练参数数量：0.

在汇聚层之后进行了局部响应归一化，LRN的动机如下图所示⁴。

3. 第二个卷积层
   滤波器：使用 2 个大小为 5 × 5 × 48 × 128 的卷积核；
   步长： = 1；
   零填充： = 2；
   特征映射结果：得到 2 个大小为 27 × 27 × 128 的特征映射组；
   解释：对于每一个通道，经过滤波器卷积后，得到深度为 128 的一个映射特征。这里H=27，K=5，S=1，P=2，则每个映射特征大小（宽 × 高）为 27 × 27，从而每个通道的映射特征大小为 27 × 27 × 128。
   可训练参数数量：(5 × 5 × 48 + 1) × 128 × 2 个可训练参数。
   解释：对于每个通道的每个深度，都是由一个 5 × 5 × 48 的卷积核卷积而来，因此每个深度有 5 × 5 × 48 个权重，除此之外每个深度还对应 1 个偏置，从而共有 5 × 5 × 48 + 1个可训练参数，那么 2 个通道、每个通道 128 个深度共有 (5 × 5 × 48 + 1) × 128 × 2 个可训练参数。

4. 第二个汇聚层
   采样窗口及汇聚函数：使用大小为 3 × 3 的最大汇聚操作
   步长： = 2；
   特征映射结果：得到 2 个大小为 13 × 13 × 128 的特征映射组。
   解释：对于每一个通道，经过 3 × 3 的最大汇聚操作后，得到深度仍为 128 的一个映射特征（汇聚层并不会改变特征映射深度）。这里H=27，K=3，S=2，P=0，则每个映射特征大小（宽 × 高）为 13 × 13，从而每个通道的映射特征大小为 13 × 13 × 128。
   可训练参数数量：0.

在汇聚层之后进行了局部响应归一化

5. 第三个卷积层为两个路径的融合
   滤波器：使用 1 个大小为 3 × 3 × 256 × 384 的卷积核；
   步长： = 1；
   零填充： = 1；
   特征映射结果：得到 2 个大小为 13 × 13 × 192 的特征映射组。
   解释：这里的卷积操作是对两个路径的融合，即交叉了部分数据（如上图），共用一个 3 × 3 × 256 × 384 的卷积核，其中 256 = 128 + 128，前一个卷积层两个通道深度之和。
     这里不妨假设想是把前一个层的两个通道并起来合成一个深度为256的 13 × 13 的输入，经过 384 个大小为 3 × 3 × 256 的卷积核得到 1 个深度为384的映射特征，由H=13，K=3，S=1，P=1，可知该映射特征大小（宽 × 高）为 13 × 13，然后再拆成2个通道，即得到 2 个大小为 13 × 13 × 192 的特征映射组。
   可训练参数数量：(3 × 3 × 256 + 1) × 192 × 2个可训练参数。
   解释：这里不妨假设想，把共用的一个卷积核分成两个 3 × 3 × 256 × 192 的卷积核，那么对应第三个卷积层的每个通道的每一个深度有 3 × 3 × 256 个权重和 1 个偏置，从而两个通道共有 (3 × 3 × 256 + 1) × 192 × 2 个可训练参数。

6. 第四个卷积层
   滤波器：使用 2 个大小为 3 × 3 × 192 × 192 的卷积核
   步长： = 1；
   零填充： = 1；
   特征映射结果：得到 2 个大小为 13 × 13 × 192 的特征映射组；
   解释：对于每一个通道，经过滤波器卷积后，得到深度为 192 的一个映射特征。这里H=13，K=3，S=1，P=1，则每个映射特征大小（宽 × 高）为 13 × 13，从而每个通道的映射特征大小为 13 × 13 × 192。
   可训练参数数量：(3 × 3 × 192 + 1) × 192 × 2个可训练参数。
   解释：对于每个通道的每个深度，都是由一个 3 × 3 × 192 的卷积核卷积而来，因此每个深度有 3 × 3 × 192 个权重，除此之外每个深度还对应 1 个偏置，从而共有 3 × 3 × 192 + 1个可训练参数，那么 2 个通道、每个通道 192 个深度共有 (3 × 3 × 192 + 1) × 192 × 2 个可训练参数。

7. 第五个卷积层
   滤波器：使用 2 个大小为 3 × 3 × 192 × 128 的卷积核；
   步长： = 1；
   零填充： = 1；
   特征映射结果：得到 2 个大小为 13 × 13 × 128 的特征映射。
   解释：对于每一个通道，经过滤波器卷积后，得到深度为 128 的一个映射特征。这里H=13，K=3，S=1，P=1，则每个映射特征大小（宽 × 高）为 13 × 13，从而每个通道的映射特征大小为 13 × 13 × 128。
   可训练参数数量：(3 × 3 × 192 + 1) × 128 × 2个可训练参数。
   解释：对于每个通道的每个深度，都是由一个 3 × 3 × 192 的卷积核卷积而来，因此每个深度有 3 × 3 × 192 个权重，除此之外每个深度还对应 1 个偏置，从而共有 3 × 3 × 192 + 1个可训练参数，那么 2 个通道、每个通道 192 个深度共有 (3 × 3 × 192 + 1) × 128 × 2 个可训练参数。

8. 第三个汇聚层
   采样窗口及汇聚函数：使用大小为 3 × 3 的最大汇聚操作；
   步长： = 2；
   特征映射结果： 得到 2 个大小为 6 × 6 × 128 的特征映射组。
   解释：对于每一个通道，经过 3 × 3 的最大汇聚操作后，得到深度仍为 128 的一个映射特征（汇聚层并不会改变特征映射深度）。这里H=13，K=3，S=2，P=0，则每个映射特征大小（宽 × 高）为 6 × 6，从而每个通道的映射特征大小为 6 × 6 × 128。
   可训练参数数量：0.

9. 第一个全连接层
   神经元个数 ：4 096（全连接层是不分宽高深度）、4 096 和 1 000；
   可训练参数数量：(6 × 6 × 128 × 2 + 1) × 4096 个可训练参数。
   解释：全连接层的参数数量 = 上一层节点数量(汇聚之后的) x 下一层节点数量 + 偏置数量（即下一层的节点数量，全连接层的参数数量 = (6 × 6 × 128 × 2) × 4096 + 4096。

10. 第二个全连接层
    神经元个数 ：4 096个神经元；
    可训练参数数量：(4 096 + 1) × 4096 个可训练参数。
    解释：全连接层的参数数量 = 上一层节点数量 x 下一层节点数量 + 偏置数量（即下一层的节点数量)，全连接层的参数数量 = 4 096 × 4096 + 4096。

11. 第一个全连接层
    神经元个数 ：1 000个神经元；
    可训练参数数量：(4 096 + 1) × 1 000 个可训练参数。
    解释：全连接层的参数数量 = 上一层节点数量 x 下一层节点数量 + 偏置数量（即下一层的节点数量)，全连接层的参数数量 = 4 096 × 1 000 + 1 000。

  此外，AlexNet 还在前两个汇聚层之后进行了局部响应归一化（Local Re- sponse Normalization，LRN）以增强模型的泛化能力。

Inception 网络

  在卷积网络中，如何设置卷积层的卷积核大小是一个十分关键的问题。在 Inception 网络中，一个卷积层包含多个不同大小的卷积操作，称为Inception 模块。Inception 网络是由有多个 Inception 模块和少量的汇聚层堆叠而成。

  Inception 模块同时使用 1 × 1、3 × 3、5 × 5 等不同大小的卷积核，并将得到的特征映射在深度上拼接（堆叠）起来作为输出特征映射。

  图5.13给出了 v1 版本的 Inception 模块结构，采用了 4 组平行的特征抽取方 式 ，分 别 为 1 × 1 、3 × 3 、5 × 5 的 卷 积 和 3 × 3 的 最 大 汇 聚。同时，为了提高计算效率，减少参数数量，Inception 模块在进行 3 × 3、5 × 5 的卷积之前、3 × 3 的最大汇聚之后，进行一次 1 × 1 的卷积来减少特征映射的深度。如果输入特征映射之间存在冗余信息，1 × 1 的卷积相当于先进行一次特征抽取。

  Inception 网络有多个版本，其中最早的 Inception v1 版本就是非常著名的 GoogLeNet。

  GoogLeNet 由 9 个 Inception v1 模块和 5 个汇聚层以及其他一些卷积层和全连接层构成，总共为 22 层网络，如图5.14所示。

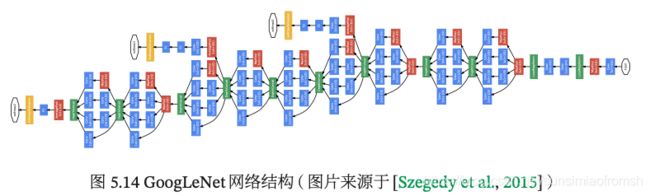
清晰图见https://nndl.github.io/v/cnn-googlenet.

  为了解决梯度消失问题，GoogLeNet 在网络中间层引入两个辅助分类器来加强监督信息。

  Inception 网络有多个改进版本，其中比较有代表性的有 Inception v3 网络。Inception v3 网络用多层的小卷积核来替换大的卷积核，以减少计算量和参数量，并保持感受野不变。具体包括：(1)使用两层 3 × 3 的卷积来替换v1中的5 × 5的卷积；(2)使用连续的 × 1和1 × 来替换 × 的卷积。

  此外，Inception v3 网络同时也引入了标签平滑以及批量归一化等优化方法进行训练。

残差网络

  残差网络(Residual Network，ResNet)通过给非线性的卷积层增加直连边(Shortcut Connection)的方式来提高信息的传播效率。

  假设在一个深度网络中，我们期望一个非线性单元(可以为一层或多层的卷积层)(; ) 去逼近一个目标函数为 h()。如果将目标函数拆分成两部分：恒等函数(Identity Function) 和残差函数(Residue Function)h() − 。

根据通用近似定理，一个由神经网络构成的非线性单元有足够的能力来近似逼近原始目标函数或残差函数，但实际中后者更容易学习。因此，原来的优化问题可以转换为：让非线性单元 (; ) 去近似残差函数 h() − ，并用 (; ) + 去逼近 h()。

  图5.15给出了一个典型的残差单元示例。残差单元由多个级联的（等宽）卷积层和一个跨层的直连边组成，再经过 ReLU 激活后得到输出。

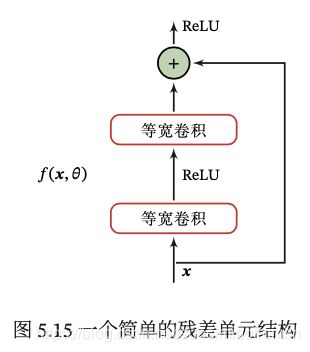
  残差网络就是将很多个残差单元串联起来构成的一个非常深的网络。和残差网络类似的还有 Highway Network。

卷积网络手动计算

1.输入层---->卷积层

  以这样一个神经网络为例⁵：输入是一个 44 的图像，经过两个 22 的卷积核进行卷积运算后，变成两个 3*3 的映射特征。

  以卷积核filter1为例（步长 = 1）：

  计算第一个卷积层神经元o11的输入：

$$\begin{array}{rl}ne{t}_{o_{11}}=& input\ast filter1\\ =& i_{11}\times h_{11}+i_{12}\times h_{12}+i_{21}\times h_{21}+i_{22}\times h_{22}\\ =& 1\times 1+0\times (-1)+1\times 1+1\times (-1)\\ =& 1\end{array}$$

  神经元o11的输出（此处使用Relu激活函数）：

$$\begin{array}{rl}ou{t}_{o_{11}}=& activators(ne{t}_{o_{11}})\\ =& ReLU(ne{t}_{o_{11}})\\ =& max\{0,ne{t}_{o_{11}}\}=1\end{array}$$

  其他神经元计算方式相同。

2.卷积层---->池化层

  计算池化层m11 的输入（取窗口为 2 * 2），池化层没有激活函数，利用最大池化：

$$\begin{array}{rl}ne{t}_{m_{11}}=& max\{o_{11},o_{12},o_{21},o_{22}\}=1\\ ou{t}_{m_{11}}=& ne{t}_{m_{11}}=1\end{array}$$

3.池化层---->全连接层

  池化层的输出到flatten层把所有元素“拍平”，然后到全连接层。

4.全连接层---->输出层

  全连接层到输出层就是正常的神经元与神经元之间的邻接相连，通过softmax函数计算后输出到output，得到不同类别的概率值，输出概率值最大的即为该图片的类别。

  来看一个卷积神经网络输出的具体手算的例子：

step 1.卷积过程（利用互相关运算）

Channel 1

$$\left[\begin{array}{ccc}0& 1& 2\\ 3& 4& 5\\ 6& 7& 8\end{array}\right]\otimes \left[\begin{array}{cc}0& 1\\ 2& 3\end{array}\right]=\left[\begin{array}{cc}19& 25\\ 37& 43\end{array}\right]$$

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]\otimes \left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]=\left[\begin{array}{cc}37& 47\\ 67& 77\end{array}\right]$$

净输入

$$\begin{array}{rl}{Z}^1=& \sum _{d=1}^2{W}^{1,d}\otimes X^d+b^1\\ =& \left[\begin{array}{cc}19& 25\\ 37& 43\end{array}\right]+\left[\begin{array}{cc}37& 47\\ 67& 77\end{array}\right]+\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\\ =& \left[\begin{array}{cc}57& 73\\ 105& 121\end{array}\right]\end{array}$$

Channel 2

$$\left[\begin{array}{ccc}0& 1& 2\\ 3& 4& 5\\ 6& 7& 8\end{array}\right]\otimes \left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]=\left[\begin{array}{cc}27& 37\\ 57& 67\end{array}\right]$$

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]\otimes \left[\begin{array}{cc}2& 3\\ 4& 5\end{array}\right]=\left[\begin{array}{cc}49& 63\\ 91& 105\end{array}\right]$$

净输入

$$\begin{array}{rl}{Z}^2=& \sum _{d=1}^2{W}^{2,d}\otimes X^d+b^2\\ =& \left[\begin{array}{cc}27& 37\\ 57& 67\end{array}\right]+\left[\begin{array}{cc}49& 63\\ 91& 105\end{array}\right]+\left[\begin{array}{cc}2& 2\\ 2& 2\end{array}\right]\\ =& \left[\begin{array}{cc}78& 102\\ 150& 174\end{array}\right]\end{array}$$

step 2. 激活函数（利用ReLU函数）

$$Y^1=ReLU(Z^1)=max(0,Z^1)=\left[\begin{array}{cc}57& 73\\ 105& 121\end{array}\right]$$

$$Y^2=ReLU(Z^2)=max(0,Z^2)=\left[\begin{array}{cc}78& 102\\ 150& 174\end{array}\right]$$

step 3. 汇聚过程（利用采样窗口为2*2的最大汇聚）

Channel 1

$$ou{t}^1=max(57,73,105,121)=121$$

Channel 2

$$ou{t}^2=max(78,102,150,174)=174$$

从而输出结果为 $(121,174)$。

卷积神经网络的反向传播手动计算（神烦，没太看懂，全凭猜）

  先给各位读者推荐一些链接，万一没看懂博主写的，赶紧换一个大佬的康康！

Charlotte77https://www.cnblogs.com/charlotte77/p/7783261.html
刘建平Pinardhttps://www.cnblogs.com/pinard/p/6494810.html
小村长https://blog.csdn.net/Lu597203933/article/details/46575871

  传统的神经网络是全连接形式的，如果进行反向传播，只需要由下一层对前一层不断的求偏导，即求链式偏导就可以求出每一层的误差敏感项，然后求出权重和偏置项的梯度，即可更新权重。而卷积神经网络有两个特殊的层：卷积层和池化层。

  不失一般性，第 $l-1$ 层共有 $D$ 个特征映射，第 $l$ 层的第 $p(1\le q\le P)$ 个特征映射净输入

$$Z^{(l,p)}=\sum _{d=1}^D{W}^{(l,p,d)}\otimes X^{(l-1,d)}+b^{(l,p)}$$

其中 $W^{(l,p,d)}$ 和 $b^{(l,p)}$ 为卷积核和偏置。第 $l$ 层中共有 $P\times D$ 个卷积核和 $P$ 个偏置。

  损失函数 $\mathcal{L}$ 关于第 $l$ 层的卷积核 $W^{(l,p,d)}$ 的偏导数为

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial W^{(l,p,d)}}=& \frac{\partial \mathcal{L}}{\partial Z^{(l,p)}}\otimes X^{(l-1,d)}\\ =& {\delta }^{(l,p)}\otimes X^{(l-1,d)}\end{array}$$

  损失函数 $\mathcal{L}$ 关于第 $l$ 层的第 $p$ 个偏置 $b^{(l,p)}$ 的偏导数为（通常的做法是将 ${\delta }^{(l,p)}$ 的各个子矩阵的项分别求和，）

$$\frac{\partial \mathcal{L}}{\partial b^{(l,p)}}=\sum _{i,j}{[{\delta }^{(l,p)}]}_{i,j}$$

汇聚层的反向传播

  当第 $l+1$ 层为汇聚层时，因为汇聚层是下采样操作，$l+1$ 层的每个神经元的误差项 对应于第 层的相应特征映射的一个区域。根据链式法则，第 $l$ 层的第 $p$ 个特征映射的误差项 ${\delta }^{(l,p)}$，只需要将 $l+1$ 层对应特征映射的误差项 ${\delta }^{(l+1,p)}$ 进行上采样操作（获得和第 $l$ 层大小一样的矩阵），再和第 $l$ 层特征映射的激活值偏导数逐个元素相乘，就得到了 ${\delta }^{(l,p)}$.

  第 $l$ 层的第 $p$ 个特征映射的误差项 ${\delta }^{(l,p)}$ 的具体推导过程如下：

$${\delta }^{(l,p)}=f_l^{\prime }(Z^{(l,p)})\odot upsample({\delta }^{(l+1,p)})$$

其中 $f_l^{\prime }(Z^{(l,p)})$ 为为第 $l$ 层使用的激活函数导数带入第 $l$ 层加权加偏置后的值，$upsample$ 为上采样函数，与汇聚层中使用的下采样操作刚好相反：

• 如果下采样是最大汇聚，误差项 ${\delta }^{(l+1,p)}$ 中每个值会直接传递到上一层对应区域中的最大值所对应的神经元，该区域中其他神经元的误差项都设为 0；
• 如果下采样是平均汇聚，误差项 ${\delta }^{(l+1,p)}$ 中每个值会被平均分配到上一层对应区域中的所有神经元上。
• 例子：
  

卷积层的反向传播

  当 $l+1$ 层为卷积层时，假设特征映射净输入 $Z^{(l+1,p)}$，其中第 $p(1\le q\le P)$ 个特征映射净输入

$$Z^{(l+1,p)}=\sum _{d=1}^D{W}^{(l+1,p,d)}\otimes X^{(l-1,d)}+b^{(l+1,p)}$$

其中 $W^{(l+1,p,d)}$ 和 $b^{(l+1,p)}$ 为第 $l+1$ 层的卷积核和偏置。第 $l+1$ 层中共有 $P\times D$ 个卷积核和 $P$ 个偏置。

  第 $l$ 层的第 $d$ 个特征映射的误差项 ${\delta }^{(l,d)}$ 的具体推导过程如下：

$${\delta }^{(l,d)}=f_l^{\prime }(Z^{(l)})\odot \sum _{p=1}^P(rot180(W^{(l+1,p,d)}))\tilde{\otimes }{\delta }^{(l+1,p)}$$

其中 $\tilde{\otimes }$ 为宽卷积。以下的例子解释一下宽卷积 $\tilde{\otimes }$：

  在误差项矩阵外面加一圈0，再将卷积核旋转180度，作用到误差项矩阵上。

  来看一个卷积神经网络输出的具体手算的例子：

  第一题的解答在上个模块里，第二题解答如下：

LeNet-5（汇聚层为最大汇聚）代码

  代码源自《动手学习深度学习》⁶。

import mxnet
from mxnet import gluon, init, nd, autograd
from mxnet.gluon import data as gdata
import d2lzh as d2l
from mxnet.gluon import loss as gloss, nn
import time
import random
import numpy as np

mnist_train = gdata.vision.FashionMNIST(train=True)
#mnist_test = gdata.vision.FashionMNIST(train=False)

# 建立网络
def get_net():
    net = nn.Sequential()
    net.add(nn.Conv2D(channels=6, kernel_size=5, activation='sigmoid'),
            # C1卷积层，输出通道channels为6，滤波器高*宽5*5，激活函数activation为sigmoid
            nn.MaxPool2D(pool_size=2, strides=2),
            # S2汇聚层，这里用的是最大汇聚，采样窗口pool_size为2*2，步长strides为2
            nn.Conv2D(channels=16, kernel_size=5, activation='sigmoid'),
            # C3卷积层，输出通道channels为16，滤波器高*宽5*5，激活函数activation为sigmoid
            nn.MaxPool2D(pool_size=2, strides=2),
            # S4汇聚层，这里用的是最大汇聚，采样窗口pool_size为2*2，步长strides为2
            nn.Dense(120, activation='sigmoid'),
            # C6卷积层，输出通道channels为120，输出结果高*宽1*1，滤波器高*宽5*5，激活函数activation为sigmoid
            # Dense会默认将(批量大小, 通道, 高, 宽)形状的输入转换成(批量大小, 通道 * 高 * 宽)形状的输入
            nn.Dense(84, activation='sigmoid'),
            # F6全连接层，激活函数activation为sigmoid
            nn.Dense(10)
            # 输出层，10个径向基函数组成
            )
    ctx = d2l.try_gpu()
    mxnet.random.seed(0)
    net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier())
    return net
    

# 将数据分成k折
def get_k_fold_data(k, i, X, y):
    assert k > 1
    fold_size = X.shape[0] // k
    X_train, y_train = None, None
    for j in range(k):
        idx = slice(j * fold_size, (j + 1) * fold_size)
        X_part, y_part = X[idx, :], y[idx]
        if j == i:
            X_valid, y_valid = X_part, y_part
        elif X_train is None:
            X_train, y_train = X_part, y_part
        else:
            X_train = nd.concat(X_train, X_part, dim=0)
            y_train = nd.concat(y_train, y_part, dim=0)
    return X_train, y_train, X_valid, y_valid
    

#计算批量数据的accuracy
def evaluate_accuracy(data_iter, net):
    """Evaluate accuracy of a model on the given data set."""
    acc_sum, n = nd.array([0]), 0
    for X, y in data_iter:
        y = y.reshape((1,-1))
        y = y.astype('float32')
        acc_sum += (net(X).argmax(axis=1) == y).sum()
        n += y.size
    acc_sum.wait_to_read()
    return acc_sum.asscalar() / n
    

# 训练模型，基于d2l.train_ch3修改而来
def train_ch3_modify(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None):
    """Train and evaluate a model with CPU."""
    train_ls, test_ls = [], []
    for epoch in range(num_epochs):
        for X, y in train_iter:
            train_acc_echo, n_echo = 0.0, 0
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            if trainer is None:
                sgd(params, lr, batch_size)
            else:
                trainer.step(batch_size)
            y = y.reshape((1,-1))
            y = y.astype('float32')
            train_acc_echo += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n_echo += y.size
        train_ls.append(train_acc_echo/n_echo)
        test_ls.append(evaluate_accuracy(test_iter, net))
    return train_ls, test_ls
   

# 进行k折交叉验证
def k_fold(k, X_train, y_train, num_epochs,
           learning_rate, weight_decay, batch_size):
    train_l_sum, valid_l_sum = 0.0, 0.0
    num_workers=0
    loss = gloss.SoftmaxCrossEntropyLoss() #采用交叉熵作为损失函数
    train_l_mean, valid_l_mean=0.0, 0.0
    transformer = []
    transformer += [gdata.vision.transforms.ToTensor()]
    transformer = gdata.vision.transforms.Compose(transformer)
    for i in range(k):
        X_train, y_train, X_valid, y_valid = get_k_fold_data(k, i, X_train, y_train)        
        train_kfold=gdata.ArrayDataset(X_train,y_train)
        valid_kfold=gdata.ArrayDataset(X_valid,y_valid)    
        train_iter = gdata.DataLoader(train_kfold.transform_first(transformer),    
                                  batch_size, shuffle=False,
                                  num_workers=num_workers)
        valid_iter = gdata.DataLoader(valid_kfold.transform_first(transformer),
                             batch_size, shuffle=False,
                                 num_workers=num_workers)
        
        net = get_net()
        trainer = gluon.Trainer(net.collect_params(), 'sgd', {
     'learning_rate': learning_rate})
        #训练模型，返回的是各epoch下的accuracy
        train_ls, valid_ls = train_ch3_modify(net, train_iter, valid_iter, loss, num_epochs, batch_size, None,
              None, trainer)

        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        train_l_mean += np.array(train_ls)
        valid_l_mean += np.array(valid_ls)
        optimal_epoch=np.mat(valid_ls).argmax(axis=1)+1        
        print('fold %d, train acc %f, valid acc %f, optimal num_epochs %d'
              % (i, train_ls[-1], valid_ls[-1], optimal_epoch))
        
        #作图
        d2l.semilogy(range(1,num_epochs+1), train_ls, 'epochs', 'acc',
                       range(1,num_epochs+1), valid_ls,
                         ['train', 'valid'])
    
    return train_l_sum / k, valid_l_sum / k, train_l_mean / k, valid_l_mean / k
    

k, num_epochs, lr, weight_decay, batch_size = 2, 200, 0.5, 0, 100 
#k为交叉验证折数，lr为learning rate

train_features, train_labels = mnist_train[0:5000] #为加速展示，我这里只取了前5000个cases

#通过交叉验证选取最优的num_epochs（耗时约388秒）
start=time.time()
train_l, valid_l, train_l_fold, valid_l_fold = k_fold(k, train_features, train_labels, num_epochs, lr,
                          weight_decay, batch_size)

optimal_epoch_kfold=np.argmax(valid_l_fold)+1
print('%d-fold validation: avg train acc %f, avg valid acc %f, optimal num_epochs %d'
      % (k, train_l, valid_l, optimal_epoch_kfold))

#作图
d2l.semilogy(range(1,num_epochs+1), list(train_l_fold), 'epochs', 'acc',
                       range(1,num_epochs+1), list(valid_l_fold),
                         ['train', 'valid'])

'%.2f sec' % (time.time()-start)
#其他超参数（learning_rate、bathc_size等）的确定可类似操作

结果不放出来，由于每台电脑设备id不同，会导致结果不同。

说明&致谢

  神经网络的计算真的好烦哦，但是还是要耐耐心心地算一遍，罢说了，继续研究上次前馈神经网络的代码去了，神将网络博大精深！神经网络屠我毛发！在此，特要感谢本人深度学习的授课老师Ms.L提供的资料和教学。Come and Join Us Machine Learning！
  接下来计划学习循环神经网络理论知识及代码，并书写读书笔记。

参考资料

---

1. CSDN博主：scxyz_. 【CNN】理解卷积神经网络中的通道 channel
   https://blog.csdn.net/sscc_learning/article/details/79814146 ↩︎

2. CSDN博主：saw009. 关于LeNet-5卷积神经网络 S2层与C3层连接的参数计算的思考？？？
   https://blog.csdn.net/saw009/article/details/80590245 ↩︎

3. AlexNet中的参数数量
   https://vimsky.com/article/3664.html ↩︎ ↩︎

4. CSDN博主：Microstrong0305. 在AlexNet中LRN 局部响应归一化的理解
   https://blog.csdn.net/program_developer/article/details/79430119 ↩︎

5. 博客园博主：Charlotte77.【深度学习系列】卷积神经网络详解(二)——自己手写一个卷积神经网络https://www.cnblogs.com/charlotte77/p/7783261.html ↩︎

6. Aston Zhang and Zachary C. Lipton and Mu Li and Alexander J. Smola. Dive into Deep Learning（动手学习深度学习）: chapter 3
   http://zh.gluon.ai/index.html. ↩︎