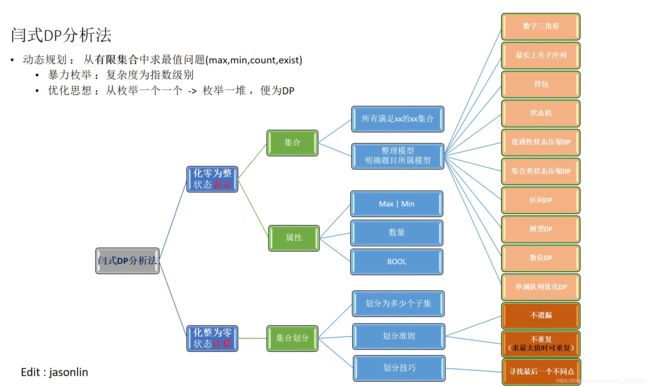
acwing26动态规划
动态规划以前写过博客,最近发现以前的博客存在逻辑不完善的地方。借着学习acwing的算法的机会,再重新审视一下自己存在的问题。
动态规划
背包问题
最长公共子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N 和 M。
第二行包含一个长度为 N 的字符串,表示字符串 A。
第三行包含一个长度为 M 的字符串,表示字符串 B。
字符串均由小写字母构成。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N,M≤1000
输入样例:
4 5
acbd
abedc
输出样例:
3
这题之前写过博客,也算dp的一道入门题了。这次从集合的角度去理解问题,希望能有更深的感悟。
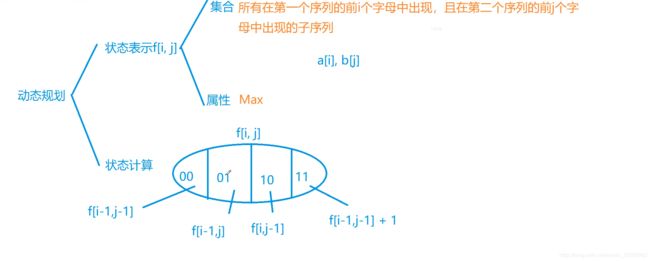
先对问题分类:
集合表示:f[i][j]表示a的前i个字母,和b的前j个字母的最长公共子序列长度
集合划分:以a[i]a[i],b[j]b[j]是否包含在子序列当中为依据,因此可以分成四类:
- a[i]不在,b[j] 不在:max=f[i−1][j−1]。
- a[i]不在,b[j] 在:看似是max=f[i−1][j] , 无法实际上无法用f[i−1][j]表示,因为f[i−1][j]表示的是在a的前i-1个字母中出现,并且在b的前j个字母中出现,此时b[j]不一定出现,这与条件不完全相等,条件给定是a[i]一定不在子序列中,b[j]一定在子序列当中,但仍可以用f[i−1][j]来表示,原因就在于条件给定的情况被包含在f[i−1][j]中,即条件的情况是f[i−1][j]的子集,而求的是max,所以对结果不影响。例如:要求a,b,c的最大值可以这样求: max(max(a,b),max(b,c))虽然b被重复使用,但仍能求出max,求max只要保证不漏即可。
- a[i] 在,b[j] 不在 原理同②。
- a[i]在,b[j] 在:max=f[i−1][j−1]+ 1。
- 实际上,在计算时,①包含在②和③的情况中,所以①不用考虑
#include 石子合并(区间DP)
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2 堆,代价为 4,得到 4 5 2, 又合并 1,2 堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2,3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300
输入样例:
4
1 3 5 2
输出样例:
22
区间 DP 常用模版:
所有的区间dp问题,第一维都是枚举区间长度,一般 len = 1 用来初始化,枚举从 len = 2 开始,第二维枚举起点 i (右端点 j 自动获得,j = i + len - 1)
for (int i = 1; i <= n; i++)
{
dp[i][i] = 初始值
}
for (int len = 2; len <= n; len++) //区间长度
for (int i = 1; i + len - 1 <= n; i++)
{
//枚举起点
int j = i + len - 1; //区间终点
for (int k = i; k < j; k++)
{
//枚举分割点,构造状态转移方程
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
#include 记忆化搜索:
#include 最长上升子序列二分板子
#include 最短编辑距离
给定两个字符串 A 和 B,现在要将 A 经过若干操作变为 B,可进行的操作有:
删除–将字符串 A 中的某个字符删除。
插入–在字符串 A 的某个位置插入某个字符。
替换–将字符串 A 中的某个字符替换为另一个字符。
现在请你求出,将 A 变为 B 至少需要进行多少次操作。
输入格式
第一行包含整数 n,表示字符串 A 的长度。
第二行包含一个长度为 n 的字符串 A。
第三行包含整数 m,表示字符串 B 的长度。
第四行包含一个长度为 m 的字符串 B。
字符串中均只包含大写字母。
输出格式
输出一个整数,表示最少操作次数。
数据范围
1≤n,m≤1000
输入样例:
10
AGTCTGACGC
11
AGTAAGTAGGC
输出样例:
4

一、状态表示
1.状态表示:dp[i][j]指的是把前i个字母变成b中前j个字母的集合,因为是两重循环枚举,可以包含所有组合。
2.属性:对于每个dp[i][j]进行的所有操作中,操作次数最少的方案的操作数。
二、状态计算
1.对任意一个i 串和 j 串,它们的子串为ii串和jj串,改变内部子串某一元素,如果使得 i串 和 j串 相等,那么它的解一定相等于 ii串 最后一个元素a[i] 变成 jj串最后一个元素的解,所以只需要对任意串 i , j :

讨论使它们相等的最后一步:
(1)添加:如果a串添加当前字母变得与 j 串相同,说明a[i]已经与此时与 a[j-1]相同,即:dp[i][j]=dp[i][j-1] + 1
(2)删除:如果a串删除当前字母变得与 j 串相同,说明a[i-1]已经与a[j]相同,即:dp[i][j]=dp[i-1][j] + 1
(3)替换:如果当前结尾字母不同,则前i-1与j-1已经相同,即:dp[i][j]=dp[i-1][j-1] + 1
(4)a[i]与a[j] 已经相同,更新之前的状态:dp[i][j]=dp[i-1][j-1]
#include 编辑距离
和上题一样,多个字符串先存起来,求一个在Limit操作次数内实现的方案数。
#include计数问题(数位统计DP)
给定两个整数 a 和 b,求 a 和 b 之间的所有数字中 0∼9 的出现次数。
例如,a=1024,b=1032,则 a 和 b 之间共有 9 个数如下:
1024 1025 1026 1027 1028 1029 1030 1031 1032
其中 0 出现 10 次,1 出现 10 次,2 出现 7 次,3 出现 3 次等等…
输入格式
输入包含多组测试数据。
每组测试数据占一行,包含两个整数 a 和 b。
当读入一行为 0 0 时,表示输入终止,且该行不作处理。
输出格式
每组数据输出一个结果,每个结果占一行。
每个结果包含十个用空格隔开的数字,第一个数字表示 0 出现的次数,第二个数字表示 1 出现的次数,以此类推。
数据范围
0
1 10
44 497
346 542
1199 1748
1496 1403
1004 503
1714 190
1317 854
1976 494
1001 1960
0 0
输出样例:
1 2 1 1 1 1 1 1 1 1
85 185 185 185 190 96 96 96 95 93
40 40 40 93 136 82 40 40 40 40
115 666 215 215 214 205 205 154 105 106
16 113 19 20 114 20 20 19 19 16
107 105 100 101 101 197 200 200 200 200
413 1133 503 503 503 502 502 417 402 412
196 512 186 104 87 93 97 97 142 196
398 1375 398 398 405 499 499 495 488 471
294 1256 296 296 296 296 287 286 286 247
数位dp分类讨论:
比如说我要找[1,abcdefg]中的数中1出现的个数
就得先求1在每一个位置上出现的次数
比如我要找第4位上出现的1的数有几个
就是要找满足 1 <= xxx1yyy <= abcdefg
(1) xxx∈[000,abc-1] , yyy∈[000,999] :如果前三位没填满,则后三位就可以随便填 :ans += abc*1000
(2)xxx == abc :如果前三位填满了,后三位怎么填取决于当前这一位
- if(d<1) yyy不存在 , ans += 0
- if(d==1) yyy∈[000,efg] , ans += efg+1
- if(d>1) yyy∈[000,999] , ans += 1000
#include没有上司的舞会(树形DP)
状态表示:
f[i][j]:其表示的是以 i 为树根,及其左右子树可以符合无上司条件的个数最大值,j 用来表示根节点 i 是不是存在与这个最大值当中。
比如求红圈内的无上司最大值:

首先需要递归的求出s1,s2的最大值。
然后当前u树的答案个数一定是对u树的子树里的个数以某种方式累加求和。
状态计算:
若当前u结点不选,子结点可选可不选
f[u][0]=∑max(f[si,0],f[si,1])
若当前u结点选,子结点一定不能选
f[u][1]=∑(f[si,0])
#include整数划分(计数类dp)
一个正整数 n 可以表示成若干个正整数之和,形如:n=n1+n2+…+nk,其中 n1≥n2≥…≥nk,k≥1。
我们将这样的一种表示称为正整数 n 的一种划分。
现在给定一个正整数 n,请你求出 n 共有多少种不同的划分方法。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示总划分数量。
由于答案可能很大,输出结果请对 109+7 取模。
数据范围
1≤n≤1000
输入样例:
5
输出样例:
7
完全背包同思路推导。
f[i][j]表示的是用前 i 个数,组成 j 这个正整数,其中可行的方案数量。


#include 第二种思路的f[i][j]表示的是总和为 i ,并且由 j 个数组成的方案数。

当最小值为1时,去掉最后一个1 可以得到f[i][j]=f[i-1][j-1]。
当最小值大于1时,给 j 个数每个数减去1,f[i][j]=f[i-j][j],这两种方案一一对应。
将两种情况加和即为f[1][j]的答案。
而最终的答案则是把f[n][1]到f[n][n]求和。
#include