均匀带电体的场强的计算
问题探讨
- 问题背景:已知均匀带电细棒外一点的场强,已知均匀带电圆环轴线上一点的场强,已知均匀带电圆盘轴线上一点的场强,试求均匀带电圆球轴线上一点的场强。
- 基本解题思路:利用点电荷的场强计算式: E ⃗ = 1 4 π ϵ 0 q r 2 e r ⃗ \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r^2}\vec{e_r} E=4πϵ01r2qer;再利用积分求和即可得到答案。
- 问题引导
- 如图所示,设真空中有一均匀带电细棒AB的电荷线密度为 λ \lambda λ; P P P为 A B AB AB外的一点,它到 A B AB AB的距离为 a a a, A P AP AP、 B P BP BP与 y y y轴的夹角分别为 θ 1 \theta_1 θ1, θ 2 \theta_2 θ2,求带电棒在 P P P点产生的场强。

- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
解:
在 A B AB AB棒上任取一段微元(电荷元) d y dy dy,故有此所带的电荷量为 d q = λ d y dq=\lambda dy dq=λdy,
故其在 P P P点所产生的场强为 d E ⃗ = 1 4 π ϵ 0 d q r 2 e r ⃗ = 1 4 π ϵ 0 λ d y r 2 e r ⃗ d\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{dq}{r^2}\vec{e_r}=\frac{1}{4\pi\epsilon_0}\frac{\lambda dy}{r^2}\vec{e_r} dE=4πϵ01r2dqer=4πϵ01r2λdyer
注: e r ⃗ \vec{e_r} er表示由施力电荷指向受力电荷的单位矢量。
因为这是一个二维场,故有在 x , y x,y x,y轴上的投影分别为(化标量)
d E x = d E s i n θ = λ s i n θ 4 π ϵ 0 d y dE_x=dEsin\theta=\frac {\lambda sin\theta}{4\pi\epsilon_0}dy dEx=dEsinθ=4πϵ0λsinθdy
d E y = d E c o s θ = λ c o s θ 4 π ϵ 0 d y dE_y=dEcos\theta=\frac{\lambda cos\theta}{4\pi\epsilon_0}dy dEy=dEcosθ=4πϵ0λcosθdy
式子中的 θ \theta θ为 d E ⃗ d\vec{E} dE与 y y y轴的夹角, r r r为线元 d y dy dy到 P P P点的距离。
由图易得,变量 θ , y , r \theta,y,r θ,y,r之间的关系为
y = − a c o t θ y=-acot\theta y=−acotθ, r = a s i n θ = a c s c θ r=\frac{a}{sin\theta}=acsc\theta r=sinθa=acscθ
故有 d y = a d θ s i n 2 θ = a c s c 2 θ d θ dy=\frac{ad\theta}{sin^2\theta}=acsc^2\theta d\theta dy=sin2θadθ=acsc2θdθ
所以,
d E x = λ 4 π ϵ 0 a s i n θ d θ dE_x=\frac{\lambda}{4\pi \epsilon_0a}sin\theta d\theta dEx=4πϵ0aλsinθdθ
d E y = λ 4 π ϵ 0 a c o s θ d θ dE_y=\frac{\lambda}{4\pi \epsilon_0a}cos\theta d\theta dEy=4πϵ0aλcosθdθ
对二式积分,即可得到在 P P P点处的 X , Y X,Y X,Y方向上的合场强
即 E x = ∫ θ 1 θ 2 d E x = ∫ θ 1 θ 2 λ s i n θ 4 π ϵ 0 a d θ = λ 4 π ϵ 0 a ( c o s θ 1 − c o s θ 2 ) E_x=\int^{\theta_2}_{\theta_1} dE_x=\int^{\theta_2}_{\theta_1}\frac{\lambda sin\theta}{4\pi \epsilon_0a}d\theta=\frac{\lambda}{4\pi \epsilon_0a}(cos\theta_1-cos\theta_2) Ex=∫θ1θ2dEx=∫θ1θ24πϵ0aλsinθdθ=4πϵ0aλ(cosθ1−cosθ2)
E y = ∫ θ 1 θ 2 d E y = ∫ θ 1 θ 2 λ c o s θ 4 π ϵ 0 a d θ = λ 4 π ϵ 0 a ( s i n θ 2 − s i n θ 1 ) E_y=\int^{\theta_2}_{\theta_1} dE_y=\int^{\theta_2}_{\theta_1}\frac{\lambda cos\theta}{4\pi \epsilon_0a}d\theta=\frac{\lambda}{4\pi \epsilon_0a}(sin\theta_2-sin\theta_1) Ey=∫θ1θ2dEy=∫θ1θ24πϵ0aλcosθdθ=4πϵ0aλ(sinθ2−sinθ1)
故在 P P P点处的场强:
E ⃗ = E x i ⃗ + E y j ⃗ = λ 4 π ϵ 0 a [ ( c o s θ 1 − c o s θ 2 ) i ⃗ + ( s i n θ 2 − s i n θ 1 ) j ⃗ ] \vec{E}=E_x\vec{i}+E_y\vec{j}=\frac{\lambda}{4\pi \epsilon_0a}[(cos\theta_1-cos\theta_2)\vec{i}+(sin\theta_2-sin\theta_1)\vec{j}] E=Exi+Eyj=4πϵ0aλ[(cosθ1−cosθ2)i+(sinθ2−sinθ1)j]
如若细棒可认为无限长,则可有 θ 1 = 0 , θ 2 = π \theta_1=0,\theta_2=\pi θ1=0,θ2=π
即得细棒在 P P P点处的场强 E ⃗ = E x i ⃗ = λ 2 π ϵ 0 a i ⃗ \vec{E}=E_x\vec{i}=\frac{\lambda}{2\pi \epsilon_0a}\vec{i} E=Exi=2πϵ0aλi
方向:该处场强的方向与细棒垂直。
- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
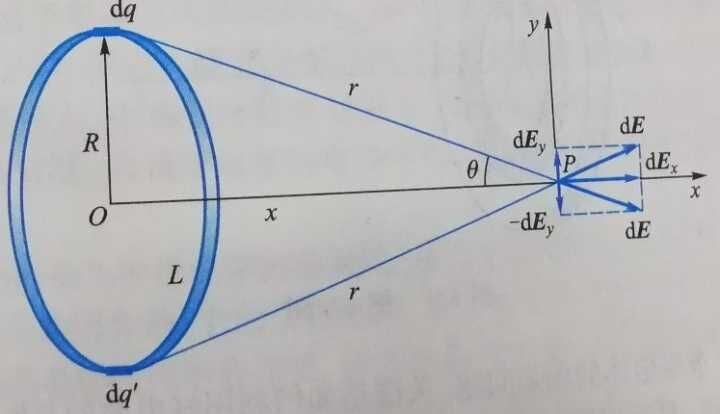
- 如图所示,该均匀带电圆盘 L L L的半径为 R R R,所带电荷为 q q q,则求垂直于环面,且过环心的 x x x轴上任一点 P P P的场强。
- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
解:
在圆环 L L L任取一电荷元 d q dq dq,则其在 P P P点处产生的场强为: d E ⃗ = d q 4 π ϵ 0 r 2 e r ⃗ d\vec{E}=\frac{dq}{4\pi\epsilon_0r^2}\vec{e_r} dE=4πϵ0r2dqer
显然由图可得,这是二维场,电荷对称分布。
所以,使得对称方向上的成对等量电荷元 q , q ′ q,q' q,q′在 y y y方向上的场强等大反向,相互抵消。
于是, P P P点处的场强仅仅只有 x x x方向上的分量。
即 d q dq dq在 P P P点处场强在 x x x方向上的投影为:
c o s θ = x r cos\theta=\frac{x}{r} cosθ=rx 此处 x , r x,r x,r均可认为是常量。
d E = d E x c o s θ = d q 4 π ϵ 0 r 2 c o s θ = x d q 4 π ϵ 0 r 3 dE=dE_xcos\theta=\frac{dq}{4\pi \epsilon_0 r^2}cos\theta=\frac{xdq}{4\pi \epsilon_0 r^3} dE=dExcosθ=4πϵ0r2dqcosθ=4πϵ0r3xdq
对上式进行积分,即可得到 P P P点处的场强大小
E = E x = ∫ d E x = ∮ x d q 4 π ϵ 0 r 3 = x q 4 π ϵ 0 r 3 = x q 4 π ϵ 0 ( x 2 + R 2 ) 3 2 E=E_x=\int dE_x=\oint \frac{xdq}{4\pi \epsilon_0 r^3}=\frac{xq}{4\pi \epsilon_0 r^3}=\frac{xq}{4\pi \epsilon_0 (x^2+R^2)^\frac{3}{2}} E=Ex=∫dEx=∮4πϵ0r3xdq=4πϵ0r3xq=4πϵ0(x2+R2)23xq
即可得到一些推论:
当 P P P点位于环心时( x = 0 x=0 x=0),其产生场强为0;
当 P P P点距离环心无限远时( x > > R x>>R x>>R),其产生的场强为 E = q 4 π ϵ 0 x 2 E=\frac{q}{4\pi \epsilon_0x^2} E=4πϵ0x2q
方向:该处场强的方向与圆环平面垂直。
- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
- 如图所示,有一半径为 R R R的均匀带电圆盘,其电荷面密度为 σ \sigma σ,试求过盘心,且垂直于盘面的轴上的场强。

- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
解:
该带电圆盘可等效为由半径为0至半径为 R R R的带电圆环构成的。
可在圆盘内取一半径为 r r r,宽为 d r dr dr的环带作为电荷元,其所带电荷量为 d q = σ 2 π r d r dq=\sigma 2\pi rdr dq=σ2πrdr
这是一个二维场,由于电荷对称分布,所以只有 x x x轴方向上的场强分量。
所以,在 P P P点处的场强大小为 d E = x d q 4 π ϵ 0 ( x 2 + r 2 ) 3 2 = σ x r d r 2 ϵ 0 ( x 2 + r 2 ) 3 2 dE=\frac{xdq}{4\pi \epsilon_0 (x^2+r^2)^\frac{3}{2}}=\frac{\sigma xrdr}{2\epsilon_0 (x^2+r^2)^\frac{3}{2}} dE=4πϵ0(x2+r2)23xdq=2ϵ0(x2+r2)23σxrdr
对上式进行积分,即可得到整个圆盘在 P P P点处产生的场强大小:
E = ∫ d E = ∫ 0 R σ x r d r 2 ϵ 0 ( x 2 + r 2 ) 3 2 = σ 2 ϵ 0 [ 1 − x ( x 2 + R 2 ) 1 2 ] E=\int dE=\int ^{R} _{0}\frac{\sigma xrdr}{2\epsilon_0 (x^2+r^2)^\frac{3}{2}}=\frac{\sigma}{2\epsilon_0}[1-\frac{x}{(x^2+R^2)^\frac{1}{2}}] E=∫dE=∫0R2ϵ0(x2+r2)23σxrdr=2ϵ0σ[1−(x2+R2)21x]
则有当圆盘无限大时,即 R > > x R>>x R>>x时,有 E ⃗ = σ 2 ϵ i ⃗ \vec{E}=\frac{\sigma}{2\epsilon}\vec{i} E=2ϵσi
方向:该处场强的方向与圆盘平面垂直。
- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
- 如图所示,设真空中有一均匀带电细棒AB的电荷线密度为 λ \lambda λ; P P P为 A B AB AB外的一点,它到 A B AB AB的距离为 a a a, A P AP AP、 B P BP BP与 y y y轴的夹角分别为 θ 1 \theta_1 θ1, θ 2 \theta_2 θ2,求带电棒在 P P P点产生的场强。
- 解决问题
-
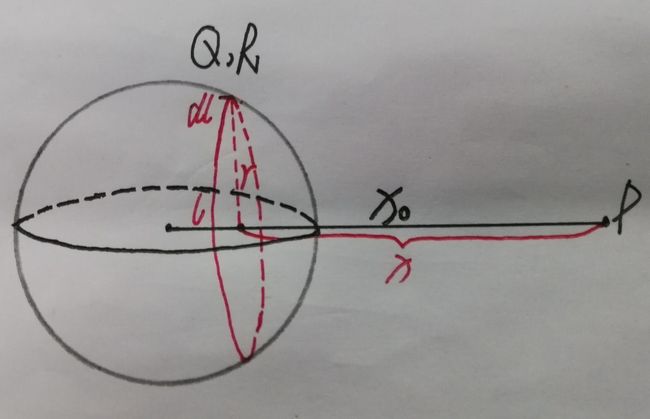
如图所示,有一半径为R的均匀实心带电圆球,所带电量为 Q Q Q,试求过球心,其轴线上距离球心 x 0 x_0 x0处 P P P点的场强。
- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
解:
该带电圆球可等效为由半径为0至半径为 R R R的带电圆盘构成的。
可在圆球内取一距离圆心为 l l l,半径为 r r r,宽为 d l dl dl的盘块作为电荷元。
R 2 = r 2 + l 2 R^2=r^2+l^2 R2=r2+l2 所以, r 2 = R 2 − l 2 r^2=R^2-l^2 r2=R2−l2
则其所带电荷量 d q = 3 Q 4 π R 3 π r 2 d l = 3 Q 4 R 3 r 2 d l dq=\frac{3Q}{4\pi R^3} \pi r^2dl=\frac{3Q}{4R^3}r^2dl dq=4πR33Qπr2dl=4R33Qr2dl
所以,电荷面密度 σ = 3 Q 4 π R 3 d l \sigma=\frac{3Q}{4\pi R^3}dl σ=4πR33Qdl
所取圆盘距球心距离为 l l l,距离 P P P点为 x x x,则 x = x 0 − l x=x_0-l x=x0−l
即有,在 P P P处的场强大小为 d E = σ 2 ϵ 0 [ 1 − x ( x 2 + r 2 ) 1 2 ] = 3 Q 8 ϵ 0 π R 3 [ 1 − x 0 − l ( ( x 0 − l ) 2 + R 2 − l 2 ) ) 1 2 ] d l dE=\frac{\sigma}{2\epsilon_0}[1-\frac{x}{(x^2+r^2)^\frac{1}{2}}]=\frac{3Q}{8\epsilon_0 \pi R^3}[1-\frac{x_0-l}{((x_0-l)^2+R^2-l^2))^\frac{1}{2}}]dl dE=2ϵ0σ[1−(x2+r2)21x]=8ϵ0πR33Q[1−((x0−l)2+R2−l2))21x0−l]dl
对上式积分即可得到整个圆球体在 P P P点处产生的场强大小:
E = ∫ d E = ∫ − R R 3 Q 8 ϵ 0 π R 3 [ 1 − x 0 − l ( ( x 0 − l ) 2 + R 2 − l 2 ) ) 1 2 ] d l = ∫ − R R 3 Q 8 ϵ 0 π R 3 ( x 0 2 − 2 x 0 l + R 2 + x 0 − l − 2 x 0 l + x 0 2 + R 2 ) d l = 3 Q 8 ϵ 0 π R 3 ( R 3 3 x 0 2 − ( − R 3 3 x 0 2 ) ) = Q 4 ϵ 0 π x 0 2 E=\int dE=\int ^{R} _{-R}\frac{3Q}{8\epsilon_0 \pi R^3}[1-\frac{x_0-l}{((x_0-l)^2+R^2-l^2))^\frac{1}{2}}]dl=\int^R _{-R}\frac{3Q}{8\epsilon_0 \pi R^3}(\frac{x_0^2-2x_0l+R^2+x_0-l}{-2x_0l+x_0^2+R^2})dl=\frac{3Q}{8\epsilon_0 \pi R^3}(\frac{R^3}{3x_0^2}-(-\frac{R^3}{3x_0^2}))=\frac{Q}{4\epsilon_0 \pi x_0^2} E=∫dE=∫−RR8ϵ0πR33Q[1−((x0−l)2+R2−l2))21x0−l]dl=∫−RR8ϵ0πR33Q(−2x0l+x02+R2x02−2x0l+R2+x0−l)dl=8ϵ0πR33Q(3x02R3−(−3x02R3))=4ϵ0πx02Q
方向: P P P点的场强方向与轴线方向相同
- 注意:(1)选好点电荷;(2)尽量使矢量积分简化(化矢量积分为标量积分,注意多变量统一)
-