算法图解读后感(理解概念)简单查找和二分查找、数组和链表、 递归、快速排序、散列表、广度优先搜索、迪特斯特拉算法
目录
-
- 第一节 简单查找和二分查找
- 第二节 数组和链表
- 第三节 递归
- 第四节 快速排序
- 第五节 散列表
- 第六节 广度优先搜索
- 第七节、迪特斯特拉算法
第一节 简单查找和二分查找
简单查找
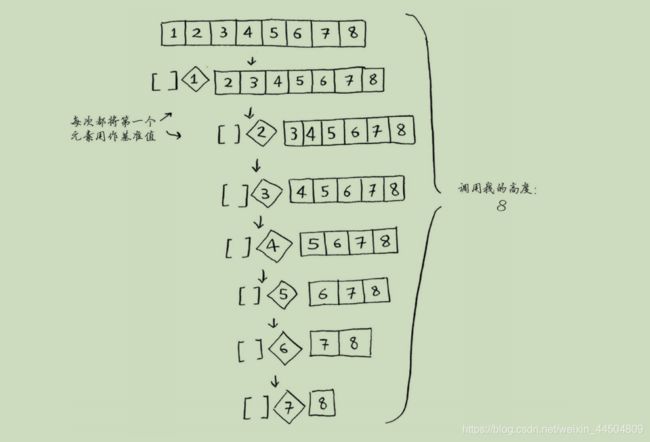
有n个数,在最糟糕的情况下需要遍历n次,也就是O(n)。
二分查找
取中间的数进行比较,偏小取左边区域中间的数再比较,偏大取右边区域中间的数再比较,直到找到数值或者找不到为止。有n个数,在最糟糕的情况下需要遍历logn(在算法中,logn
指log2n)次,也就是O(logn)。
案例,在一个无序的集合中找到某个数值
public class BinarySearch {
public static void main(String[] args) {
ArrayList<Integer> list = new ArrayList<>();
list.add(1);
list.add(5);
list.add(9);
list.add(12);
list.add(4);
list.add(35);
list.add(2);
binarySearch(list,9);
}
public static void binarySearch(List<Integer> list , Integer num){
list.sort(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
int size = list.size();
int lowindex = 0;
int highindex = size - 1;
int count = 0 ; // 计数器,看看找了多少次?
while (lowindex <= highindex){
int middleindex = (lowindex + highindex) / 2;
int middlenum = list.get(middleindex);
if(middlenum > num ){
highindex = middleindex - 1;
}else if(middlenum < num){
lowindex = middleindex + 1;
}else {
System.out.println("第" + ++count + "次找到了数值" + middlenum);
return;
}
count++;
}
System.out.println("找了"+ count + "次");
System.out.println("没有找到");
}
}
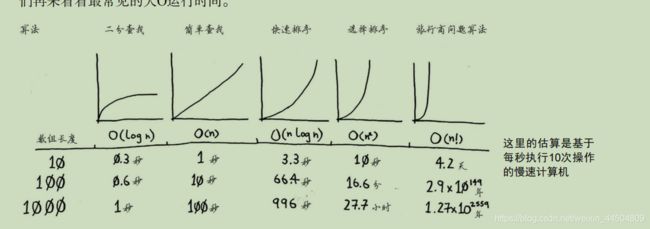
大O表示法
大O表示法指算法在最糟糕的情况下的运行时间。(时间复杂度)
常见的有: O(n) ;O(logn) ;O(n^2) ;O(n!) ;O(n*logn) ;O(1) 。
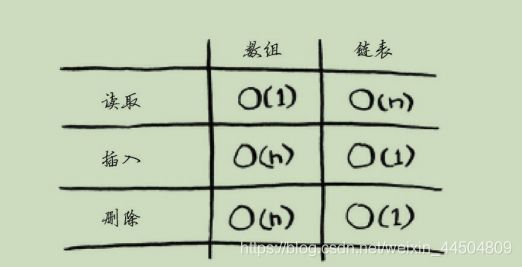
第二节 数组和链表
随机访问和顺序访问
顺序访问意味着从第一个元素开始逐个地读取元素。链表只能顺序访问:要读取链表的第十个元素,得先读取前九个元素,并沿链接找到第十个元素。随机访问意味着可直接跳到第十个元素。本书经常说数组的读取速度更快,这是因为它们支持随机访问。很多情况都要求能够随机访问。
public class SelectSort {
public static void main(String[] args) {
int[] arr = {
3,4,1,2,4,7,2,1,5,9};
int[] arrsort = selectSort(arr);
System.out.println(Arrays.toString(arrsort));
}
/*/**
* @Description: 选择排序:前面的数值和后面所有的数值进行比较 ,O(n^2)
* @Param: [arr]
* @return: int[]
* @Date: 2021/4/26
*/
public static int[] selectSort(int[] arr){
for (int i = 0; i < arr.length; i++) {
for (int j = i + 1; j < arr.length; j++) {
if(arr[i] > arr[j]){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
}
使用递归实现选择排序
public class SelectSort {
public static void main(String[] args) {
int[] arr = {
3,4,1,2,4,7,2,1,5,9};
int[] arr2 = selectSort2(arr, 0, arr.length - 1);
System.out.println( Arrays.toString(arr2));
}
/**
* @Description: 使用递归求解选择排序
* @Param: [arr, start, end]
* @return: int[]
* @Date: 2021/4/27
*/
public static int[] selectSort2(int[] arr,int start, int end){
if(start > end){
return arr;
}
int i = start;
int j = end;
int init = arr[i];
while (i < j){
if (init > arr[i]){
int temp = arr[i];
arr[i] = init;
init = temp;
arr[start] = temp;
}else{
i++;
}
}
System.out.println(Arrays.toString(arr));
selectSort2(arr,start+1,end);
return arr;
}
}
第三节 递归
递归只是让解决方案更清晰,并没有性能上的优势。
如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解。如何选择要看什么对你来说更重要。
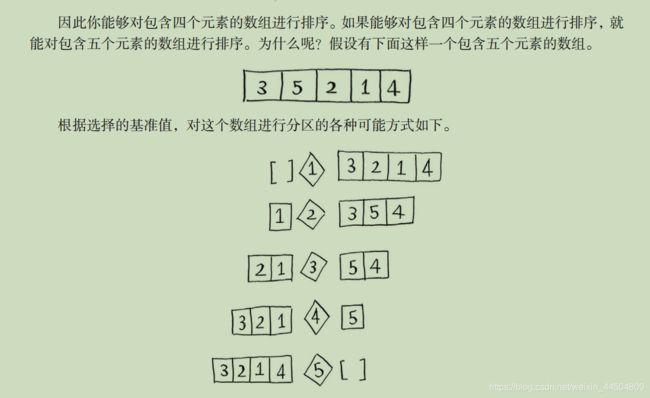
第四节 快速排序
分而治之(divide and conquer,D&C)——一种著名的递归式问题解决方法()
快速排序使用分而治之的策略。
D&C工作原理:
1、找到简单的基线条件,
2、确定如何缩小问题的规模,使其符合基线条件。
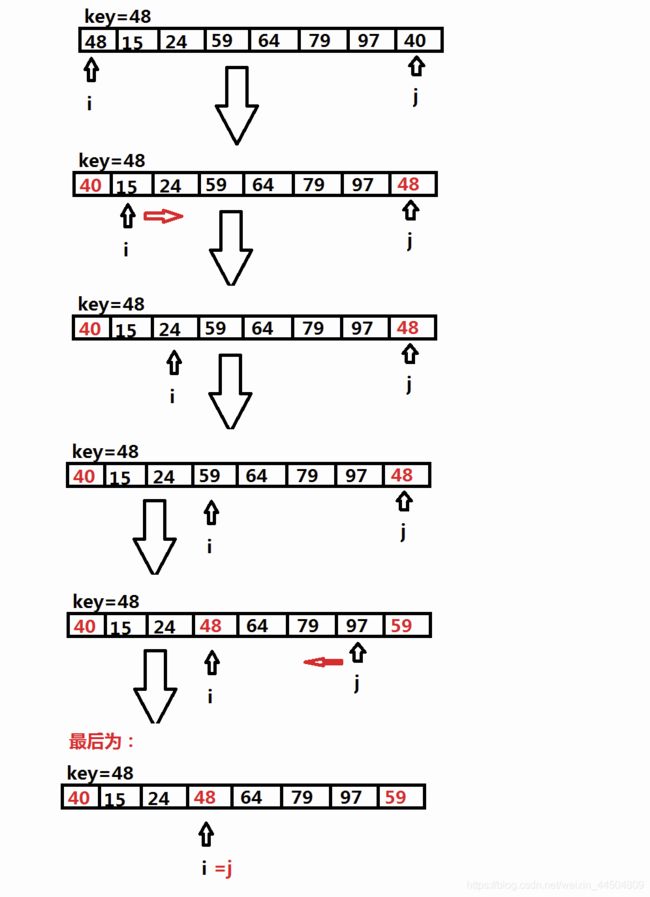
public class QuickSort {
public static void main(String[] args) {
int[] arr = {
3,4,1,2,4,7,2,1,5,9};
int[] arrs = quickSort(arr, 0, arr.length - 1);
System.out.println( Arrays.toString(arrs));
}
/*/**
* @Description: 快速排序,使用的是D&C思想
* @Param: [arr]
* @return: int[]
* @Date: 2021/4/27
*/
public static int[] quickSort(int[] arr,int start, int end){
// 分而治之,第一步:基线条件 第二步:确认如何缩小规模,使其符合基线条件
//也就是把数组分成 3 个部分,小的数组 基线条件 大的数组 (任何小的数组和大的数组再排序)
//start >= end 结束递归
if(start >= end){
return arr;
}
int i = start;
int j = end;
//基线条件,基线条件的位置会发生变化的
int init = arr[i];
boolean flag = true;
// i == j 也就是基线条件的位置,这个时候,3个部分已经分离成功
while (i != j){
if(flag){
if(init >arr[j]){
// arr[j] 小于基线条件,应该放在左边
swap(arr,i,j);
flag = false;
}else{
j--;
}
}else{
if(init < arr[i]){
// arr[i] 应该放在右边
swap(arr,i,j);
flag = true;
}else{
i++;
}
}
}
// 打印每次排序后的数组
System.out.println(Arrays.toString(arr));
// 左边的数组递归
// (注意:只是虚拟的分为3个部分,左边数组的排序依旧是调用整个数组进行排序,
// 只是右边的数组的数值都大于左边的数组,一直进行j--直到 再次遇到比基线条件小的值
quickSort(arr,start,j-1);
// 右边的数组递归,同理
quickSort(arr,i+1,end);
return arr;
}
/*/**
* @Description:交换数组位置
* @Param: [arr]
* @return: void
* @Date: 2021/4/27
*/
public static void swap(int[] arr,int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
快速排序的情况比较棘手,在最糟情况下,其运行时间为O(n^2)。与选择排序一样慢!但这是最糟情况。在平均情况下,快速排序的运行时间为O(n log n)。
平均情况和最糟情况
快速排序的性能高度依赖于你选择的基准值。假设你总是将第一个元素用作基准值,且要处 理的数组是有序的。由于快速排序算法不检查输入数组是否有序,因此它依然尝试对其进行排序。
注意,数组并没有被分成两半,相反,其中一个子数组始终为空,这导致调用栈非常长。也就是O(n),
调用栈短得多!因为你每次都将数组分成两半,所以不需要那么多递归调用。你很快就到达 了基线条件,因此调用栈短得多。
第一个示例展示的是最糟情况,而第二个示例展示的是最佳情况。在最糟情况下,栈长为 O(n),而在最佳情况下,栈长为O(log n)。
在这个示例中,层数为O(log n)(用技术术语说,调用栈的高度为O(logn)),而每层需要的时间为O(n)。因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。 在最糟情况下,有O(n)层,因此该算法的运行时间为O(n) * O(n) = O(n2)。
合并排序
public class MergeSort {
public static void main(String[] args) {
int[] arr = {
3,4,1,2,4,7,2,1,5,9};
int[] arr2 = mergeSort(arr, 0, arr.length - 1);
//System.out.println(Arrays.toString(arr2));
}
/**
* @Description: 对整个数组进行分组
* @Param: [arr, start, end]
* @return: int[]
* @Date: 2021/4/27
*/
public static int[] mergeSort(int[] arr ,int start, int end){
if(start < end){
int mid = ( start + end )/2;
//左边的数组
mergeSort(arr,start,mid);
//右边的数组
mergeSort(arr,mid+1,end);
//切割成多个数组之后合并
merge(arr,start,mid,end);
}
return arr;
}
/*
* @Description: 合并两个数组
* @Param: [arr, start, mid, end]
* @return: int[]
* @Date: 2021/4/27
*/
public static int[] merge(int[] arr,int start,int mid, int end){
// 第一个数组 [start,mid]
int n1 = mid - start + 1;
// 第二个数组 [mid + 1 , end]
int n2 = end - mid;
int[] larr = new int[n1 + 1]; // 长度需要 + 1,避免索引越界
int[] rarr = new int[n2 + 1];
//对两个数组赋值
for (int i = 0; i < n1; i++) {
larr[i] = arr[start + i];
}
// 看看有几个二分法
System.out.println(Arrays.toString(larr));
for (int i = 0; i < n2; i++) {
rarr[i] = arr[mid + 1 +i];
}
// 看看有几个二分法
System.out.println(Arrays.toString(rarr));
larr[n1] = Integer.MAX_VALUE;
rarr[n2] = Integer.MAX_VALUE;
int i = 0;
int j = 0;
for (int k = start; k <= end; k++) {
if(larr[i] <= rarr[j]){
arr[k] = larr[i];
i++; // 需要注意:如果长度不加+1,比较的时候i++ 会索引越界
}else{
arr[k] = rarr[j];
j++; // 同理
}
}
System.out.println( Arrays.toString(arr));
return arr;
}
}
第五节 散列表
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
Hash Table的查询速度非常的快,几乎是O(1)的时间复杂度。
散列表可以用作缓冲数据。
散列表适用与防止重复。
散列表冲突
一个数组的容量是有限的,如果要存储的数据超过数组的容量,那么散列表可能会将2个数据封存到同一个地址值中,这种可能性非常大。这就是散列表的冲突。如何解决,可以再哈希表的每个入口挂一个链表,保存所有数据。
由此转化为另一个问题:散列表函数的性能
前面的散列函数将所有的键都映射到一个位置,而最理想的情况是,散列函数将键均匀地映射到散列表的不同位置。如果散列表存储的链表很长,散列表的速度将急剧下降。然而,如果使用的散列函数很好,这些链表就不会很长!
避免冲突:
1、较低的填装因子; 2、良好的散列函数。
一个不错的经验规则是:一旦填装因子大于0.7,就调整散列表的长度。但是调整长度的开销很大
第六节 广度优先搜索
广度优先搜索(breadth-first search,BFS)
广度优先搜索让你能够找出两样东西之间的最短距离
广度优先搜索可回答两类问题。
第一类问题:从节点A出发,有前往节点B的路径吗?
第二类问题:从节点A出发,前往节点B的哪条路径最短?
运行时间
如果你在你的整个人际关系网中搜索芒果销售商,就意味着你将沿每条边前行(记住,边是 从一个人到另一个人的箭头或连接),因此运行时间至少为O(边数)。你还使用了一个队列,其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的,即为O(1),因此对每个人都这样做需要的总时间为O(人数)。所以,广度优先搜索的运行时间为O(人数 + 边数),这通常写作O(V + E),其中V为顶点(vertice)数,E为边数。
第七节、迪特斯特拉算法
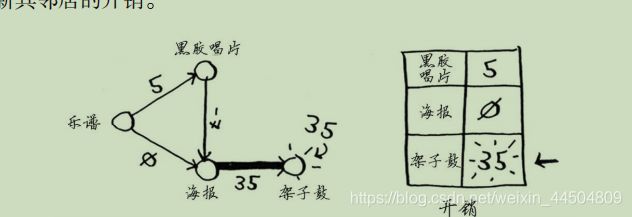
狄克斯特拉算法(Dijkstra’s algorithm)找出最快路径。
狄克斯特拉算法包含4个步骤。
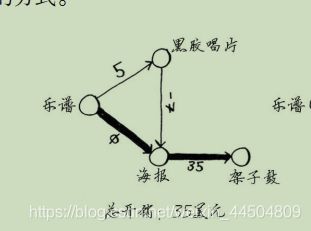
(1) 找出最便宜的节点,即可在最短时间内前往的节点。
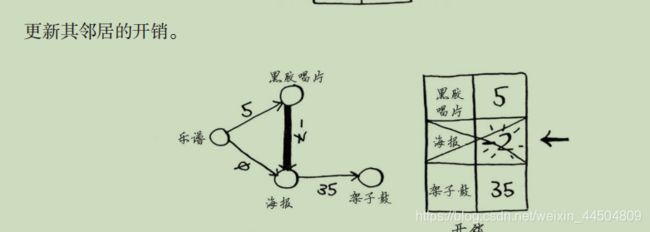
(2) 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。(这里的邻居指的是前往的对象)
(3) 重复这个过程,直到对图中的每个节点都这样做了。
(4) 计算最终路径。
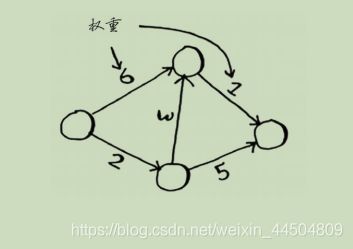
狄克斯特拉算法用于每条边都有关联数字的图,这些数字称为权重(weight)。
带权重的图称为加权图(weighted graph),不带权重的图称为非加权图(unweighted graph)。
要计算非加权图中的最短路径,可使用广度优先搜索。要计算加权图中的最短路径,可使用狄克斯特拉算法。
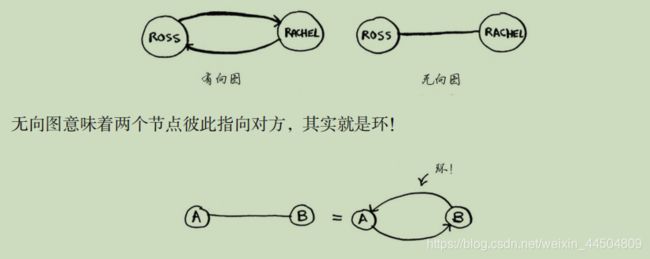
狄克斯特拉算法只适用于有向无环图
注意:
如果有负权边,就不能使用狄克斯特拉算法,在包含负权边的图中,要找出最短路径,可使用另一种算法——贝尔曼.福德算法(Bellman-Fordalgorithm)。
这是因为狄克斯特拉算法这样假设:对于处理过的海报节点,没有前往该节点的更短路径