C语言学习之路——函数递归
函数递归简介:
程序的自身函数调用成为函数递归,能把大型复杂的问题简单化,大大减少了代码量。
函数递归的只要思路在于:大事化小
函数递归的必要条件:1.写递归函数时,不能死递归,要有跳出条件,并且每次递归都要逼近跳出条件。
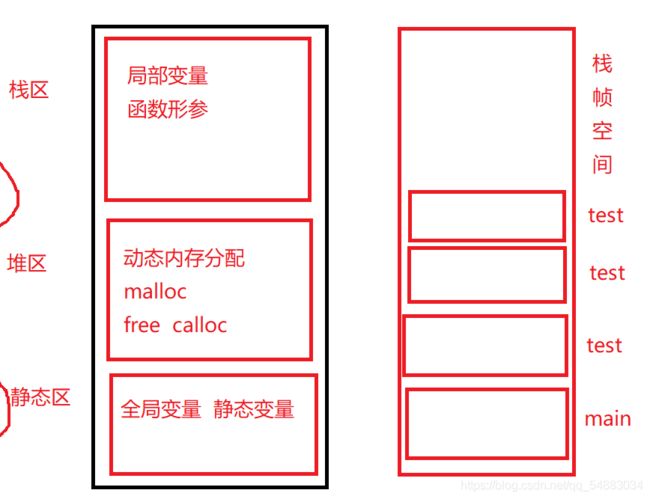
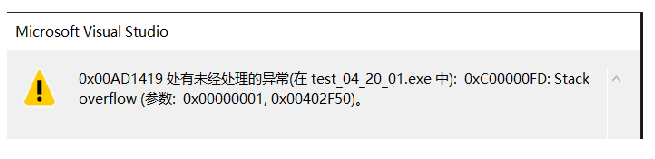
2.递归层次不能太深。,层次深的话每次的分配空间会导致栈溢出
如果不满足上述条件往往会出现栈溢出现象
#include 这里写目录标题
- 练习一: 接受一个整型值(无符号)按照顺序打印它的每一位数字,例如:1234,输出 1 2 3 4
- 练习二:编写函数不允许创建临时变量,求字符串长度 ,用函数计数器方法进行模拟,用函数递归进行模拟,用库函数进行实现
- 练习三: n的阶乘(不考虑栈溢出),先用一般方法进行求解,在使用函数递归。
- 练习四:求第n个斐波那契数(不考虑溢出),想一想这个程序是否存在缺陷,是否可以优化,缺陷在哪
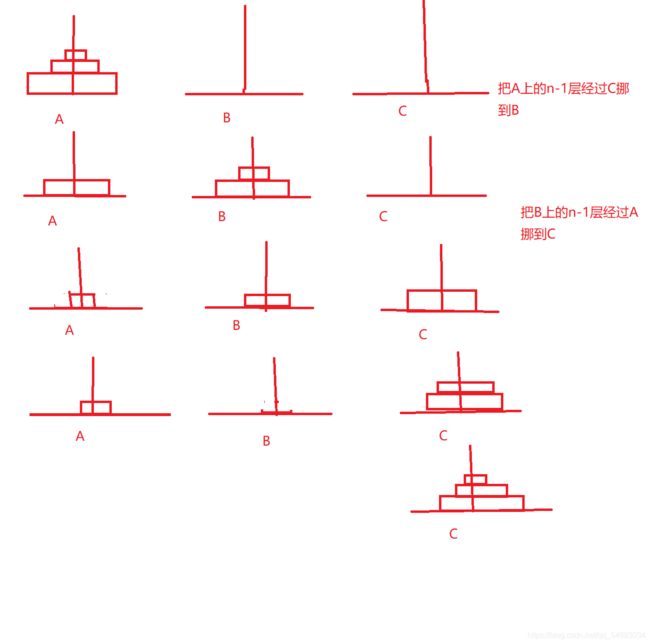
- 练习五:汉诺塔问题
- 练习六:青蛙跳台阶问题。
练习一: 接受一个整型值(无符号)按照顺序打印它的每一位数字,例如:1234,输出 1 2 3 4
练习一:
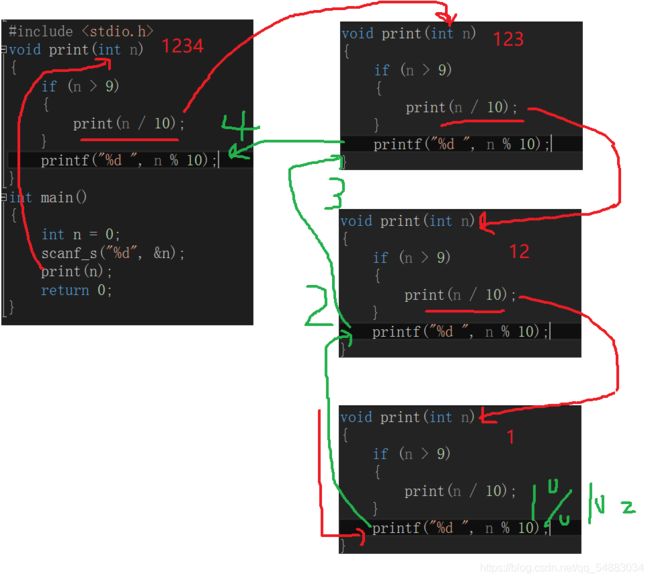
#include 具体思想:也就是依次进行模10,除10,重复工作,依次取出 4 3 2 1 然后从后向前进行返回 变成 1 2 3 4
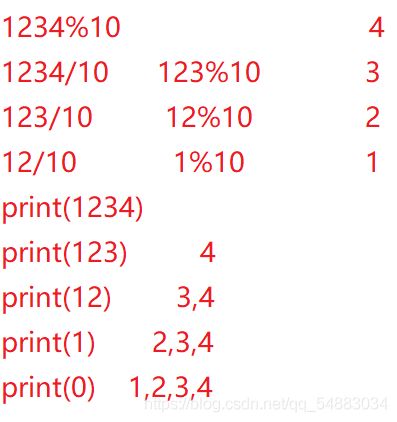
图示:
练习二:编写函数不允许创建临时变量,求字符串长度 ,用函数计数器方法进行模拟,用函数递归进行模拟,用库函数进行实现
练习二
库函数实现计算字符长度
#include 函数计数器实现计算字符串模拟
具体思路
向函数中传字符串的首地址,在没有扫描到字符串的结束标志’\0’时,使用计数器++;,直到遇到’\0’时,停止扫描,向main函数返回计数器的值。
图示
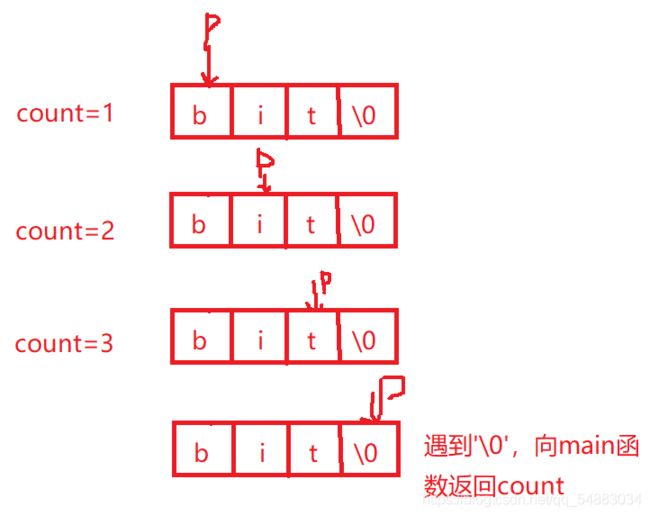
#include 用函数递归实现上述题目
具体思路:向函数中传字符串的首地址,在没有扫描到字符串的结束标志’\0’时,使用计数器++;,直到遇到’\0’时,停止扫描,向main函数返回计数器的值。
大事化小

图示
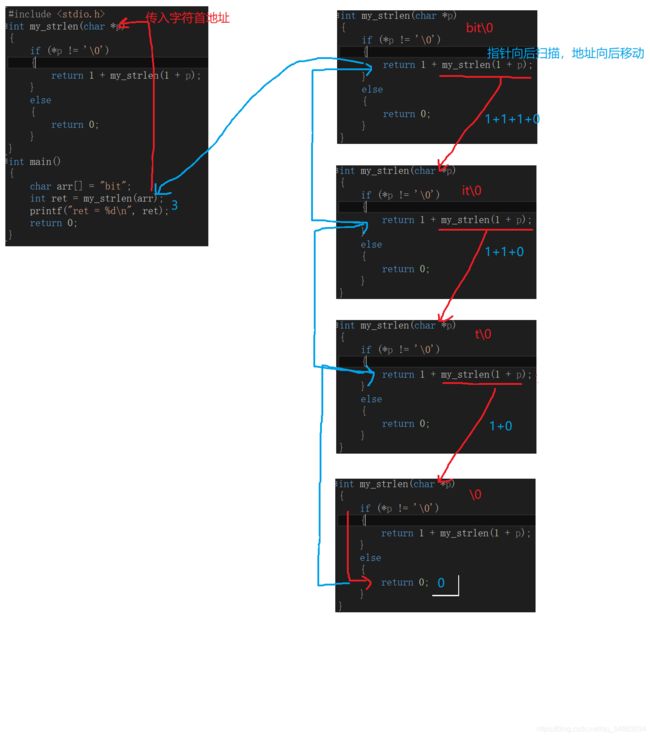
#include 练习三: n的阶乘(不考虑栈溢出),先用一般方法进行求解,在使用函数递归。
练习三
一般思路实现阶乘
思路
#include #include 练习四:求第n个斐波那契数(不考虑溢出),想一想这个程序是否存在缺陷,是否可以优化,缺陷在哪
练习四
斐波那契数列:1 1 2 3 5 8 13 21 34 55 …,也就是从第三个数开始,前两个数字开始,下一个数字等于前两个数字之和。
图示

#include 这个算法之所以不高效是因为 当往程序中输入较大值时例如50,就会计算很久,浪费时间。
优化算法
斐波那契数列
1 1 2 3 5 8 13 21 34 55 89
a b c
a b c
#include 练习五:汉诺塔问题
#include 练习六:青蛙跳台阶问题。
**第六题:**青蛙跳台阶
和斐波那契数思路相 同
#include 感谢大家的观看,如果哪有不妥的地方,或者表达不清的地方,请大佬们指点指点!