PaddlePaddle入门实践——手写数字识别

任务要求

  能够识别手写数字0~9的图像，具体来说，将手写数字的灰度图像（28像素 x 28像素）划分到10个类别中（0 ~ 9）。要求使用PaddlePaddle框架实现模型。

数据集及环境

• 数据集来源： ML领域经典数据集MNIST，包含60,000 张训练图像和 10,000 张测试图像
• 数据说明：数据分为图片和标签，图片是28*28的像素矩阵，标签为0 ~ 9共10个数字
• 运行环境：PaddlePaddle2.0 + cuda11.1 + pycharm

  Tips：PaddlePaddle2.0船新版本，新加入的高层API简化模型构建过程，便于快速上手实践！

模型搭建过程

  接下来我们主要围绕此过程进行实验，如图所示：

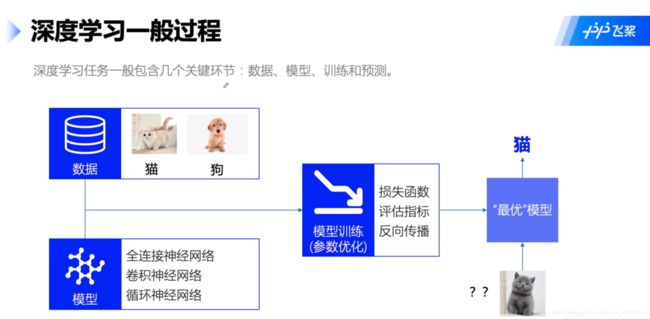
更进一步，在模型训练中，我们主要在做如下图所示的任务：

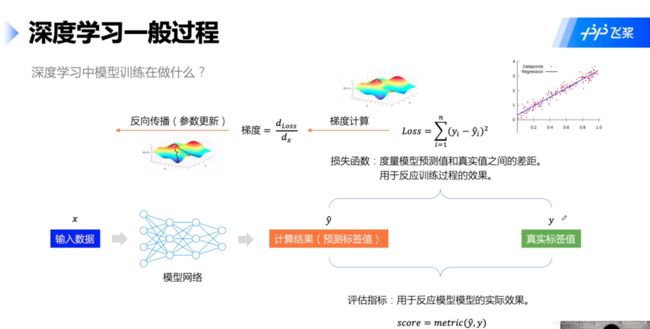
  Tips：这里的整体流程框架（为什么我们要按此流程做）可以参考李宏毅老师的regression（宝可梦）部分的讲解，关于BP神经网络（尤其是反向传播以及其中的链式求导法则）可以参考西瓜书（概括）和花书（详细）。另外，梯度优化也可参考李航老师的统计学习方法以及李宏毅老师的gradient decent部分。后续再写一个总结，这里不做展开。请各位见谅~

数据预处理

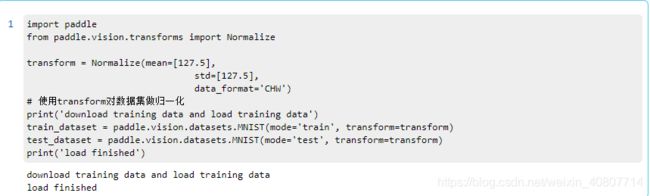
  飞桨已经内置了MNIST数据集，只需调用即可。定义数据集的训练集train_dataset和测试集test_dataset。之后使用Normalize接口对图片进行归一化处理。

import paddle
import numpy as np
import matplotlib.pyplot as plt


import paddle.vision.transforms as T

# 数据的加载和预处理
transform = T.Normalize(mean=[127.5], std=[127.5])

# 训练数据集
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)

# 评估数据集
eval_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)

print('训练集样本量: {}，验证集样本量: {}'.format(len(train_dataset), len(eval_dataset)))

  为什么要做归一化处理？这里取一张经过预处理的图片进行说明。

print('图片：')
print(type(train_dataset[0][0]))
print(train_dataset[0][0])
print('标签：')
print(type(train_dataset[0][1]))
print(train_dataset[0][1])

# 可视化展示
plt.figure()
plt.imshow(train_dataset[0][0].reshape([28,28]), cmap=plt.cm.binary)
plt.show()

如图所示，经过归一化处理过后的像素矩阵数值的范围不再是0 ~ 255，而是压缩在-1 ~ 1。显然便于之后进行运算。而针对归一化处理的方法，我们采用统一的均值和标准差值对图像的每个通道进行计算。

  而后再来关注Normalize接口都能做什么？

class paddle.vision.Normalize(mean=0.0, std=1.0, data_format='CHW', to_rgb=False, keys=None)

刚才我们已经提到了图像归一化的处理方式，而在该接口中，计算过程如下：
$$output[channel]=(input[channel]-mean[channel])/std[channel]$$
本次使用到的相关参数定义：

• mean：用于每个通道归一化的均值
• std：用于每个通道归一化的标准差值
• data_format (str, optional): 数据的格式，必须为 ‘HWC’ 或 ‘CHW’。 默认值: ‘CHW’

该方法返回归一化后的图像，返回类型为numpy ndarray(numpy的n维数组对象)。

模型组网

  现在开始设计神经网络，采用单隐层全连接网络。输入层神经元784（28像素 * 28像素），隐层512个神经元（可随意定制），输出层10个神经元（很明显这是一个多分类任务，分成0 ~ 9个数字）。

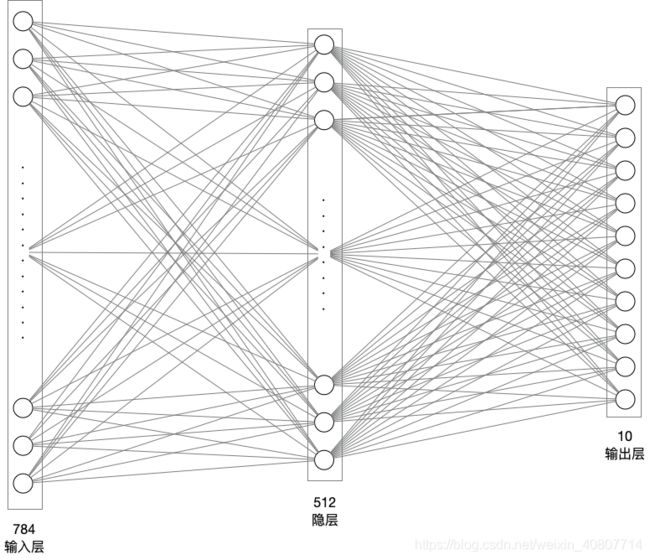
模型构建代码如下：

# 模型网络结构搭建
network = paddle.nn.Sequential(
    paddle.nn.Flatten(),           # 拉平，将 (28, 28) => (784)
    paddle.nn.Linear(784, 512),    # 隐层：线性变换层
    paddle.nn.ReLU(),              # 激活函数
    paddle.nn.Linear(512, 10)      # 输出层
)

# 模型封装
model = paddle.Model(network)

# 模型可视化
model.summary((1, 28, 28))

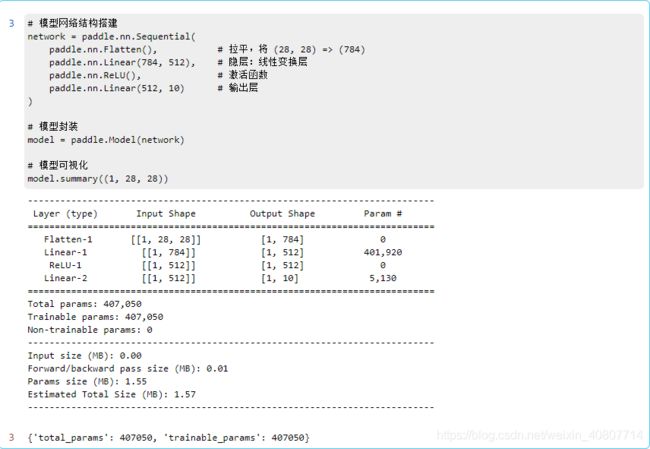
  这里我们用Sequential定义神经网络。注：Sequential接口是paddlepaddle提供的顺序容器。其中，

1.Flatten接口，将一个连续维度的Tensor展平成一维Tensor。简言之，就是将28*28像素拉平。
2. Linear接口，将隐层和输出层设置为线性变换层。即：
$$Out=XW+b$$
3. ReLU接口，用relu激活函数处理神经元经过线性变换的结果，然后作为输出值，输出到下一层
$$ReLU(x)=max(0,x)$$

之后封装模型，并做可视化确认模型构建成功与否。

训练模型

  现在开始配置损失函数、优化器以及评估指标。这里采用梯度下降法优化神经网络中的各项参数，其中我们用Adam优化器动态调整每个参数的learning rate（学习率），paddlepaddle也提供了对应的接口，建议去看接口文档，里面还有Adam算法的论文。
  然后开始训练模型。

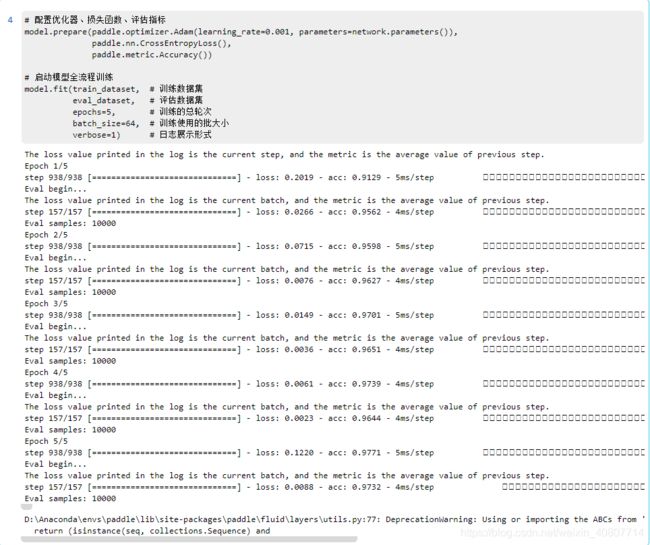
# 配置优化器、损失函数、评估指标
model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=network.parameters()),
              paddle.nn.CrossEntropyLoss(),
              paddle.metric.Accuracy())
              
# 启动模型全流程训练
model.fit(train_dataset,  # 训练数据集
          eval_dataset,   # 评估数据集
          epochs=5,       # 训练的总轮次
          batch_size=64,  # 训练使用的批大小
          verbose=1)      # 日志展示形式

评估模型

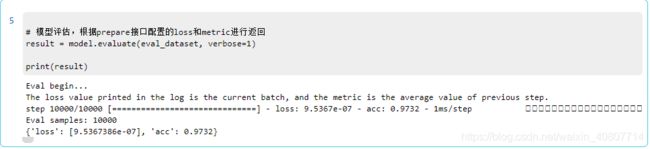
  对模型进行评估，得出accuracy（准确率）。

# 模型评估，根据prepare接口配置的loss和metric进行返回
result = model.evaluate(eval_dataset, verbose=1)

print(result)

模型预测

批量预测

  使用predict进行批量预测。
  摘自官方文档，高层API中提供了predict接口来方便用户对训练好的模型进行预测验证，只需要基于训练好的模型将需要进行预测测试的数据放到接口中进行计算即可，接口会将经过模型计算得到的预测结果进行返回。
  返回格式是一个list，元素数目对应模型的输出数目：

• 模型是单一输出：[(numpy_ndarray_1, numpy_ndarray_2, …, numpy_ndarray_n)]
• 模型是多输出：[(numpy_ndarray_1, numpy_ndarray_2, …, numpy_ndarray_n), (numpy_ndarray_1, numpy_ndarray_2, …, numpy_ndarray_n), …]
• 注：numpy_ndarray_n是对应原始数据经过模型计算后得到的预测数据，数目对应预测数据集的数目。

# 进行预测操作
result = model.predict(eval_dataset)

# 定义画图方法
def show_img(img, predict):
    plt.figure()
    plt.title('predict: {}'.format(predict))
    plt.imshow(img.reshape([28, 28]), cmap=plt.cm.binary)
    plt.show()

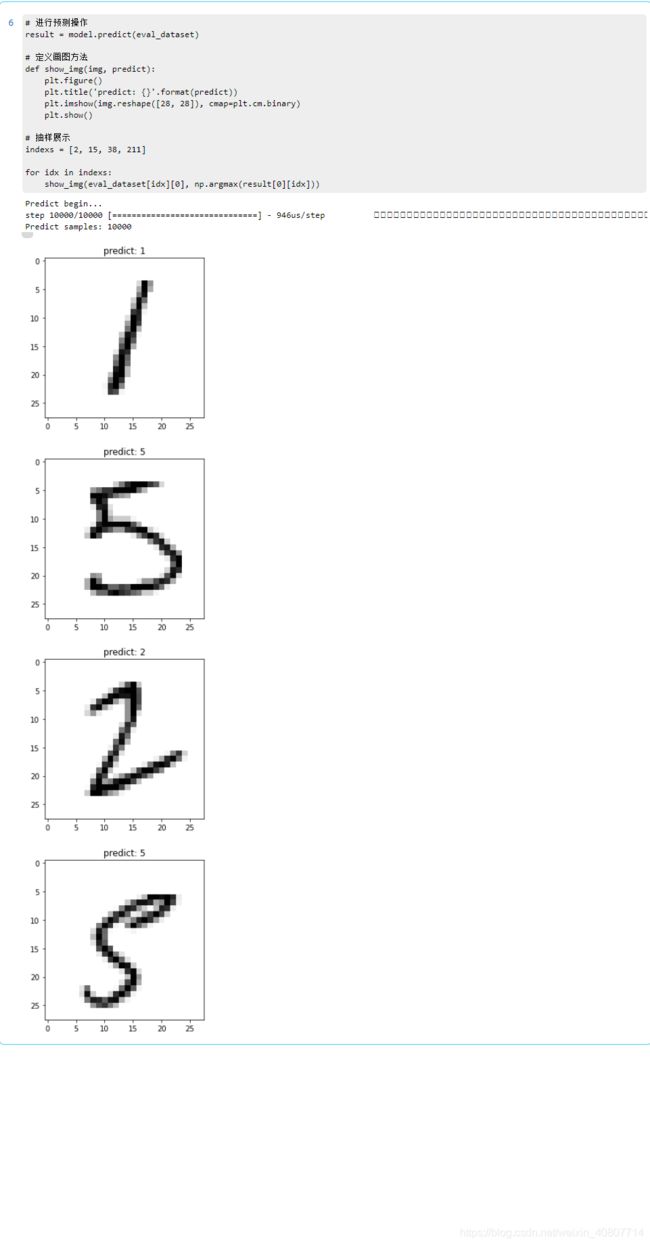
# 抽样展示
indexs = [2, 15, 38, 211]

for idx in indexs:
    show_img(eval_dataset[idx][0], np.argmax(result[0][idx]))

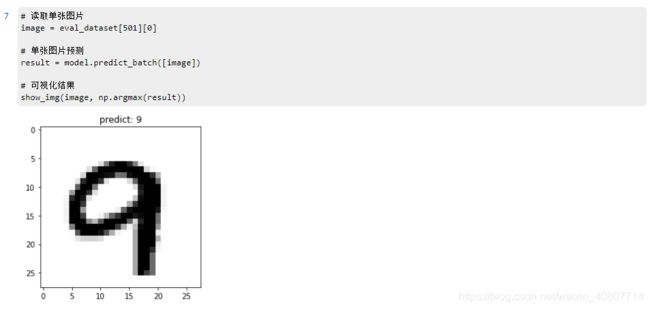
单张图片预测

  采用·model.predict_batch·来进行单张或少量多张图片的预测。

# 读取单张图片
image = eval_dataset[501][0]

# 单张图片预测
result = model.predict_batch([image])

# 可视化结果
show_img(image, np.argmax(result))

部署

保存模型

# 保存用于后续继续调优训练的模型
model.save('finetuning/mnist')

继续调优训练

from paddle.static import InputSpec


# 模型封装，为了后面保存预测模型，这里传入了inputs参数
model_2 = paddle.Model(network, inputs=[InputSpec(shape=[-1, 28, 28], dtype='float32', name='image')])

# 加载之前保存的阶段训练模型
model_2.load('finetuning/mnist')

# 模型配置
model_2.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=network.parameters()),
                paddle.nn.CrossEntropyLoss(),
                paddle.metric.Accuracy())

# 模型全流程训练
model_2.fit(train_dataset, 
            eval_dataset,
            epochs=2,
            batch_size=64,
            verbose=1)

保存预测模型

# 保存用于后续推理部署的模型
model_2.save('infer/mnist', training=False)

参考

• 飞桨官方开发文档
• 一个案例带你吃透深度学习
• CV入门——手写数字识别
• 使用飞桨完成手写数字识别模型