5.1注意力机制 Attention is all you need
文章目录
-
- 1、认知神经学中的注意力
- 2、注意力机制
-
- 注意力权重向量
- 上下文向量
- 2.1、注意力机制的变体
-
- 2.1.1 硬性注意力
- 2.1.2 键值对注意力
- 2.1.3 多头注意力
- 2.1.4 结构化注意力
- 2.1.5 指针网络
-
- Pointer Networks 的计算
- 3、self-attention 模型
-
- 计算注意力
- self-attention 是如何 解决 长距离依赖问题的呢?
- 4、情感分类中的注意力
- 5、seq2seq Attention
- 参考
本系列其他内容:
5.2各种类型的Attention_炫云云-CSDN博客
5.3 Transformer意境级讲解_炫云云-CSDN博客
5.4 self-attention以及mask操作的实现_炫云云-CSDN博客
5.5 Transformers的改进–自适应Attention
5.6 Transformer-XL讲解 意境级
5.7 Universal Transformers
5.8Reformer 意境级理解
5.9 Longformer解读
1、认知神经学中的注意力
注意力是一种人类不可或缺的复杂认知功能,指人可以在关注一些信息的同时忽略另一些信息的选择能力.在日常生活中,我们通过视觉、听觉、触觉等方式接收大量的感觉输入.但是人脑还能在这些外界的信息轰炸中有条不紊地工作,是因为人脑可以有意或无意地从这些大量输入信息中选择小部分的有用信息来重点处理,并忽略其他信息.这种能力就叫作注意力(Attention).注意力可以作用在外部的刺激(听觉、视觉、味觉等),也可以作用在内部的意识(思考、回忆等).
注意力一般分为两种:
(1) 自上而下的有意识的注意力,称为聚焦式注意力(Focus Attention). 聚焦式注意力也常称为选择性注意力(Selective Attention).聚焦式注意力是指有预定目的、依赖任务的,主动有意识地聚焦于某一对象的注意力.
(2) 自下而上的无意识的注意力,称为基于显著性的注意力(Saliency Based Attention).基于显著性的注意力是由外界刺激驱动的注意,不需要主动干预,也和任务无关.如果一个对象的刺激信息不同于其周围信息,一种无意识的“赢者通吃”(Winner-Take-All)或者门控(Gating)机制就可以把注意力转向这个对象.不管这些注意力是有意还是无意,大部分的人脑活动都需要依赖注意力,比如记忆信息、阅读或思考等.
一个和注意力有关的例子是鸡尾酒会效应.
当一个人在吵闹的鸡尾酒会上和朋友聊天时,尽管周围噪音干扰很多,他还是可以听到朋友的谈话内容,而忽略其他人的声音(聚焦式注意力).同时,如果背景声中有重要的词(比如他的名字),他会马上注意到(显著性注意力).
聚焦式注意力一般会随着环境、情景或任务的不同而选择不同的信息.比如当要从人群中寻找某个人时,我们会专注于每个人的脸部;而当要统计人群的人数时,我们只需要专注于每个人的轮廓.
Targeted Sentiment Analysis是研究target实体的情感极性分类的问题。只根据target实体,我们没有办法判断出target实体的情感极性,所以我们要根据target实体的上下文来判断。那么,第一个要解决的问题就是:如何建立target实体和上下文之间的关系。 第二个问题就是让机器学习到上下文中每个词对target实体的情感极性的贡献度。
在判断target实体的情感极性上,如下面这句话:
She began to love [miley ray cyrus]1 since 2013
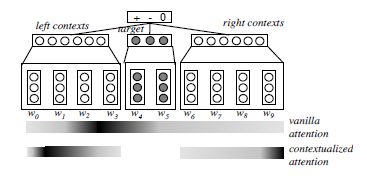
首先分析这句话,miley ray cyrus就是target实体,1代表情感是积极的。假设我们的视线是一种资源,我们只能把资源分配给更能表达情感的词上面。‘since 2013’对情感的表达没有任何意义,我们把资源分给没有任何意义的词就是一种浪费,也是十分的不合理的。而‘love’和‘’这种能表达情感的词就会吸引我们更多的注意力。于是left context和right context就可以由加权和来表示:
left context = 0.1 ∗ ’she’ + 0. 1 ∗ ’began’ + 0. 1 ⋆ ’to’ + 0. 7 ⋆ ’love’ right context = 0.1 ∗ ’since’ + 0.1 ∗ ′ 201 3 ′ + 0.8 ∗ ′ : ) ′ \begin{array}{l} \text { left context }=0.1 * \text { 'she' }+0.1^{*} \text { 'began' }+0.1^{\star} \text { 'to' }+0.7^{\star} \text { 'love' } \\ \qquad \text { right context }=0.1 * \text { 'since' } \left.+0.1 *^{\prime} 2013^{\prime}+0.8 * ':\right)^{\prime} \end{array} left context =0.1∗ ’she’ +0.1∗ ’began’ +0.1⋆ ’to’ +0.7⋆ ’love’ right context =0.1∗ ’since’ +0.1∗′2013′+0.8∗′:)′
就如同图一所示,我们的注意力应当聚焦于颜色很深的词上,颜色越深,代表它的贡献度越大。
2、注意力机制
以阅读理解任务为例,给定一篇很长的文章,然后就此文章的内容进行提问.提出的问题只和段落中的一两个句子相关,其余部分都是无关的.为了减小神经网络的计算负担,只需要把相关的片段挑选出来让后续的神经网络来处理,而不需要把所有文章内容都输入给神经网络
用 X = [ x 1 , ⋯ , x N ] ∈ R D × N \boldsymbol{X}=\left[\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}\right] \in \mathbb{R}^{D \times N} X=[x1,⋯,xN]∈RD×N 表示 N N N 组输入信息 , , , 其中 D D D 维向量 x n ∈ \boldsymbol{x}_{n} \in xn∈ R D , n ∈ [ 1 , N ] \mathbb{R}^{D}, n \in[1, N] RD,n∈[1,N] 表示一组输入信息. 为了节省计算资源,不需要将所有信息都 输入神经网络, 只需要从 X \boldsymbol{X} X 中选择一些和任务相关的信息. 注意力机制的计算可以分为两步 : 一是在所有输入信息上计算注意力分布 , , , 二是根据注意力分布来计算输入信息的加权平均.
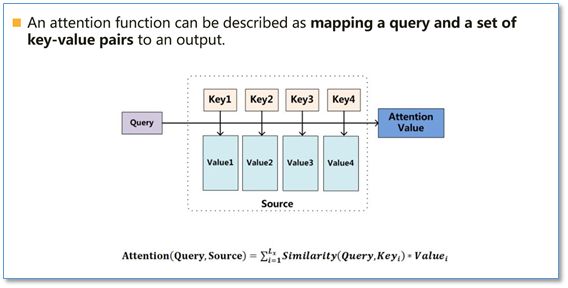
Attention函数的本质可以被描述为一个查询(query)到一系列(键key-值value)对的映射,如下图。
在计算attention时主要分为三步,第一步是将query和每个key进行相似度计算得到权重,常用的相似度函数有点积,拼接,感知机等;然后第二步一般是使用一个softmax函数对这些权重进行归一化;最后将权重和相应的键值value进行加权求和得到最后的attention。目前在NLP研究中,key和value常常都是同一个,即key=value。
注意力权重向量
为了从 N N N 个输入向量 [ x 1 , ⋯ , x N ] \left[\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}\right] [x1,⋯,xN] 中选择出和某个特定任务相关 的信息, 我们需要引入一个和任务相关的表示, 称为查询向量 ( Query Vector ),, 并通过一个打分函数来计算每个输入向量和查询向量之间的相关性.
给定一个和任务相关的查询向量 q , \boldsymbol{q}, q, 我们用注意力变量 z ∈ [ 1 , N ] z \in[1, N] z∈[1,N] 来表示被 选择信息的索引位置,即 z = n z=n z=n 表示选择了第 n n n 个输入向量. 为了方便计算, 我们 采用一种“软性”的信息选择机制. 首先计算在给定 q \boldsymbol{q} q 和 X \boldsymbol{X} X 下, 选择第 i i i 个输入向量的概率 α n , \alpha_{n}, αn,
α n = p ( z = n ∣ X , q ) = softmax ( s ( x n , q ) ) = exp ( s ( x n , q ) ) ∑ j = 1 N exp ( s ( x j , q ) ) (1) \begin{aligned} \alpha_{n} &=p(z=n \mid \boldsymbol{X}, \boldsymbol{q}) \\ &=\operatorname{softmax}\left(s\left(\boldsymbol{x}_{n}, \boldsymbol{q}\right)\right) \\ &=\frac{\exp \left(s\left(\boldsymbol{x}_{n}, \boldsymbol{q}\right)\right)}{\sum_{j=1}^{N} \exp \left(s\left(\boldsymbol{x}_{j}, \boldsymbol{q}\right)\right)} \end{aligned}\tag{1} αn=p(z=n∣X,q)=softmax(s(xn,q))=∑j=1Nexp(s(xj,q))exp(s(xn,q))(1)
其中 α n \alpha_{n} αn 称为注意力分布 ( Attention Distribution ) , s ( x , q ) , s(\boldsymbol{x}, \boldsymbol{q}) ,s(x,q) 为注意力打分函数, 可以使用以下几种方式来计算:
- 加性模型
s ( x , q ) = v ⊤ tanh ( W x + U q ) (2) s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{v}^{\top} \tanh (\boldsymbol{W} \boldsymbol{x}+\boldsymbol{U} \boldsymbol{q})\tag{2} s(x,q)=v⊤tanh(Wx+Uq)(2)
-
点积模型
s ( x , q ) = x ⊤ q (3) \quad s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top} \boldsymbol{q}\tag{3} s(x,q)=x⊤q(3) -
缩放点积模型
s ( x , q ) = x ⊤ q D (4) s(\boldsymbol{x}, \boldsymbol{q})=\frac{\boldsymbol{x}^{\top} \boldsymbol{q}}{\sqrt{D}}\tag{4} s(x,q)=Dx⊤q(4) -
双线性模型
s ( x , q ) = x ⊤ W q (5) s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top} \boldsymbol{W} \boldsymbol{q}\tag{5} s(x,q)=x⊤Wq(5)
5. 连接模型(concat )
s ( x , q ) = W [ x , q ] (6) s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{W}_{\boldsymbol{}}\left[\boldsymbol{x}, \boldsymbol{q}\right] \tag{6} s(x,q)=W[x,q](6)
其中 W , U , v \boldsymbol{W}, \boldsymbol{U}, \boldsymbol{v} W,U,v 为可学习的参数, D D D 为输入向量的维度.
理论上, 加性模型和点积模型的复杂度差不多,但是点积模型在实现上可以 更好地利用矩阵乘积,从而计算效率更高.
当输入向量的维度 D D D 比较高时, 点积模型的值通常有比较大的方差,从而导致 Softmax \operatorname{Softmax} Softmax 函数的梯度会比较小. 因此, 缩放点积模型可以较好地解决这个问题.
双线性模型是一种泛化的点积模型.假设公式(5) W = U T V \boldsymbol{W} =\boldsymbol{U}^T \boldsymbol{V} W=UTV ,双线性模型可以写为 s ( x , q ) = x ⊤ U ⊤ V q = ( U x ) ⊤ ( V q ) , s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top} \boldsymbol{U}^{\top} \boldsymbol{V} \boldsymbol{q}=(\boldsymbol{U} \boldsymbol{x})^{\top}(\boldsymbol{V} \boldsymbol{q}), s(x,q)=x⊤U⊤Vq=(Ux)⊤(Vq), 即分别对 x \boldsymbol{x} x 和 q \boldsymbol{q} q 进行线性变换后计算点积. 相比点积模型,双线性模型在计算相似度时引入了非对称性.
上下文向量
注意力分布 α n \alpha_{n} αn 可以解释为在给定任务相关的查询 q \boldsymbol{q} q 时, 第 n n n 个输入向量受关注的程度. 我们采用一种“软性”的信息选择机制对输入信息进行汇总,即
att ( X , q ) = ∑ n = 1 N α n x n = E z ∼ p ( z ∣ X , q ) [ x z ] (7) \begin{aligned} \operatorname{att}(\boldsymbol{X}, \boldsymbol{q}) &=\sum_{n=1}^{N} \alpha_{n} \boldsymbol{x}_{n} \\ &=\mathbb{E}_{\boldsymbol{z} \sim p(z \mid \boldsymbol{X}, \boldsymbol{q})}\left[\boldsymbol{x}_{z}\right] \end{aligned}\tag{7} att(X,q)=n=1∑Nαnxn=Ez∼p(z∣X,q)[xz](7)
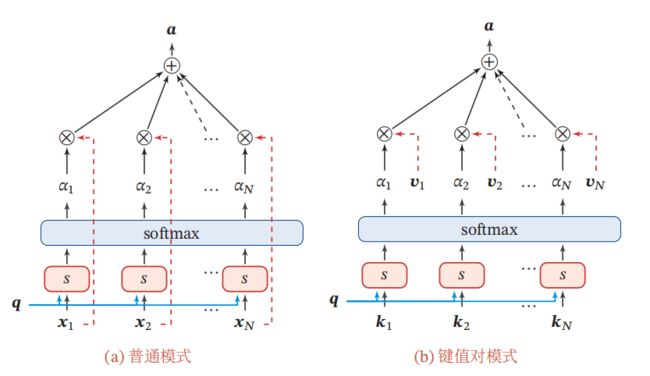
公式 (7) 称为软性注意力机制 ( Soft Attention Mechanism ). 图1a给出 软性注意力机制的示例. att ( X , q ) \operatorname{att}(\boldsymbol{X}, \boldsymbol{q}) att(X,q) 是融合了 q q q信息 X X X的上下文向量,这个向量是对 X X X的全局表征,然后可以喂给下游任务。
图 1 注 意 力 机 制 图1 注意力机制 图1注意力机制
存在问题
- 忽略了 源端或目标端 词与词间 的依赖关系
注意力机制可以单独使用,但更多地用作神经网络中的一个组件.
2.1、注意力机制的变体
除了上面介绍的基本模式外,注意力机制还存在一些变化的模型.
2.1.1 硬性注意力
公式(7)提到的注意力是软性注意力,其选择的信息是所有输入向量在注意力分布下的期望.此外,还有一种注意力是只关注某一个输入向量,叫作硬性注意力(Hard Attention).
硬性注意力有两种实现方式:
(1)一种是选取最高概率的一个输入向量,即
att ( X , q ) = x n ^ (8) \operatorname{att}(\boldsymbol{X}, \boldsymbol{q})=\boldsymbol{x}_{\hat{n}}\tag{8} att(X,q)=xn^(8)
其中 n ^ \hat{n} n^ 为概率最大的输入向量的下标,即 n ^ = arg max n = 1 α n . \hat{n}=\underset{n=1}{\arg \max } \alpha_{n} . n^=n=1argmaxαn.
(2)另一种硬性注意力可以通过在注意力分布式上随机采样的方式实现.
硬性注意力的一个缺点是基于最大采样或随机采样的方式来选择信息,使得最终的损失函数与注意力分布之间的函数关系不可导,无法使用反向传播算法进行训练.因此,硬性注意力通常需要使用强化学习来进行训练.为了使用反向传播算法,一般使用软性注意力来代替硬性注意力.
2.1.2 键值对注意力
更一般地, 我们可以用键值对 ( key-value pair) 格式来表示输入信息,其中 “键”用来计算注意力分布 α n \alpha_{n} αn,“值”用来计算聚合信息.
用 ( K , V ) = [ ( k 1 , v 1 ) , ⋯ , ( k N , v N ) ] (\boldsymbol{K}, \boldsymbol{V})=\left[\left(\boldsymbol{k}_{1}, \boldsymbol{v}_{1}\right), \cdots,\left(\boldsymbol{k}_{N}, \boldsymbol{v}_{N}\right)\right] (K,V)=[(k1,v1),⋯,(kN,vN)] 表示 N N N 组输入信息 , 给定任务相关的查询向量 q \boldsymbol{q} q 时,注意力函数为
att ( ( K , V ) , q ) = ∑ n = 1 N α n v n = ∑ n = 1 N exp ( s ( k n , q ) ) ∑ j exp ( s ( k j , q ) ) v n (9) \begin{aligned} \operatorname{att}((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}) &=\sum_{n=1}^{N} \alpha_{n} \boldsymbol{v}_{n} \\ &=\sum_{n=1}^{N} \frac{\exp \left(s\left(\boldsymbol{k}_{n}, \boldsymbol{q}\right)\right)}{\sum_{j} \exp \left(s\left(\boldsymbol{k}_{j}, \boldsymbol{q}\right)\right)} \boldsymbol{v}_{n} \end{aligned}\tag{9} att((K,V),q)=n=1∑Nαnvn=n=1∑N∑jexp(s(kj,q))exp(s(kn,q))vn(9)
其中 s ( k n , q ) s\left(\boldsymbol{k}_{n}, \boldsymbol{q}\right) s(kn,q) 为打分函数.
图1 b给出键值对注意力机制的示例. 当 K = V \boldsymbol{K}=\boldsymbol{V} K=V 时, 键值对模式就等价于普通的注意力机制.
2.1.3 多头注意力
矢头注意力 ( Multi-Head Attention ) 是利用多个查询 Q = [ q 1 , ⋯ , q M ] , \boldsymbol{Q}=\left[\boldsymbol{q}_{1}, \cdots, \boldsymbol{q}_{M}\right], Q=[q1,⋯,qM], 来并行地从输入信息中选取多组信息. 每个注意力关注输入信息的不同部分.
att ( ( K , V ) , Q ) = att ( ( K , V ) , q 1 ) ⊕ ⋯ ⊕ att ( ( K , V ) , q M ) (10) \operatorname{att}((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{Q})=\operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_{1}\right) \oplus \cdots \oplus \operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_{M}\right)\tag{10} att((K,V),Q)=att((K,V),q1)⊕⋯⊕att((K,V),qM)(10)
其中 ⨁ \bigoplus ⨁ 表示向量拼接.
2.1.4 结构化注意力
在之前介绍中,我们假设所有的输入信息是同等重要的,是一种扁平(Flat)结构,注意力分布实际上是在所有输入信息上的多项分布.但如果输入信息本身具有层次(Hierarchical)结构,比如文本可以分为词、句子、段落、篇章等不同粒度的层次,我们可以使用层次化的注意力来进行更好的信息选择 [Yang et al.,2016].此外,还可以假设注意力为上下文相关的二项分布,用一种图模型来构建更复杂的结构化注意力分布[Kim et al., 2017].
2.1.5 指针网络
动机
在某些任务中,输入严格依赖于输入,或者说输出只能从输入中选择。例如输入一段话,提取这句话中最关键的几个词语。又或是输入一串数字,输出对这些数字的排序。这时如果使用传统seq2seq模型,则decoder忽略了输入只能从输出中选择这个先验信息,Pointer Networks正是为了解决这个问题而提出的。
基本模型
Pointer Networks模型非常简洁,结构是基本的seq2seq + attention。对于传统的attention模型,在计算权重之后会对encoder的state进行加权,求得一个向量 c c c。而Pointer Networks则在计算权重之后,选择概率最大的encoder state最为输出。示意图如下:
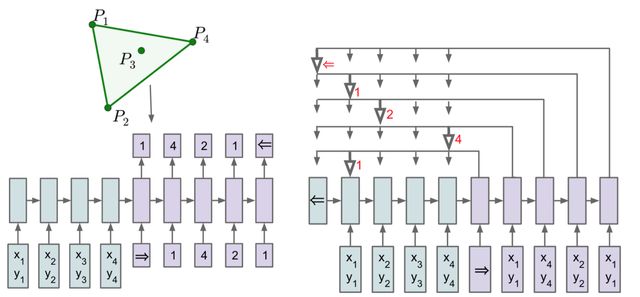
论文中使用了寻找闭包这个任务作为例子。简单的说,寻找闭包是从输入的点中找到一些点能把所有的点围起来。例如左上角图的闭包是 ( P 1 , P 2 , P 4 , P 1 ) (P_1, P_2, P_4, P_1) (P1,P2,P4,P1)。左下角则是使用传统的seq2seq模型来解决这个任务,右边则是使用Pointer Networks。其中箭头指向的则是对应时间步的输出。采用这种方式就能解决输出只能从输入中选择的问题,可谓是大道至简。
Pointer Networks 的计算
注意力机制主要是用来做信息筛选,从输入信息中选取相关的信息.注意力机制可以分为两步:一是计算注意力分布 ,二是根据 来计算输入信息的加权平均.我们可以只利用注意力机制中的第一步,将注意力分布作为一个软性的指针(pointer)来指出相关信息的位置.
指针网络 ( Pointer Network ) 是一种序列到序列模 型, 输入是长度为 N N N 的向量序列 X = x 1 , ⋯ , x N , \boldsymbol{X}=\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}, X=x1,⋯,xN, 输出是长度为 M M M 的下标序列 c 1 : M = c 1 , c 2 , ⋯ , c M , c m ∈ [ 1 , N ] , ∀ m \boldsymbol{c}_{1: M}=c_{1}, c_{2}, \cdots, c_{M}, c_{m} \in[1, N], \forall m c1:M=c1,c2,⋯,cM,cm∈[1,N],∀m
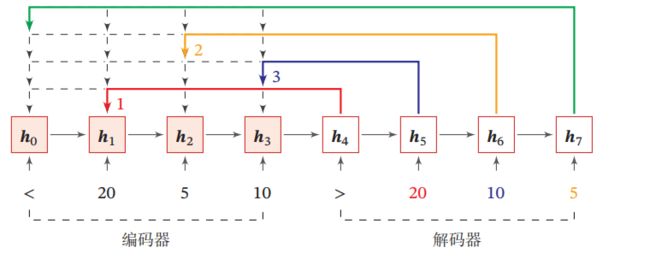
和一般的序列到序列任务不同,这里的输出序列是输入序列的下标(索引 ) ) ). 比如输入一组乱序的数字,输出为按大小排序的输入数字序列的下标. 比如输入为 20 , 5 , 10 , 20,5,10, 20,5,10, 输出为 1 , 3 , 2. 1,3,2 . 1,3,2.
条件概率 p ( c 1 : M ∣ x 1 : N ) p\left(c_{1: M} \mid \boldsymbol{x}_{1: N}\right) p(c1:M∣x1:N) 可以写为
p ( c 1 : M ∣ x 1 : N ) = ∏ m = 1 M p ( c m ∣ c 1 : ( m − 1 ) , x 1 : N ) ≈ ∏ m = 1 M p ( c m ∣ x c 1 , ⋯ , x c m − 1 , x 1 : N ) (11) \begin{aligned} p\left(c_{1: M} \mid \boldsymbol{x}_{1: N}\right) &=\prod_{m=1}^{M} p\left(c_{m} \mid c_{1:(m-1)}, \boldsymbol{x}_{1: N}\right) \\ & \approx \prod_{m=1}^{M} p\left(c_{m} \mid \boldsymbol{x}_{c_{1}}, \cdots, \boldsymbol{x}_{c_{m-1}}, \boldsymbol{x}_{1: N}\right) \end{aligned}\tag{11} p(c1:M∣x1:N)=m=1∏Mp(cm∣c1:(m−1),x1:N)≈m=1∏Mp(cm∣xc1,⋯,xcm−1,x1:N)(11)
其中条件概率 p ( c m ∣ x c 1 , ⋯ , x c ( m − 1 ) , x 1 : N ) p\left(c_{m} \mid \boldsymbol{x}_{c_{1}}, \cdots, \boldsymbol{x}_{c_{(m-1)}}, \boldsymbol{x}_{1: N}\right) p(cm∣xc1,⋯,xc(m−1),x1:N) 可以通过注意力分布来计算. 假设用一个循环神经网络对 x c 1 , ⋯ , x c m − 1 , x 1 : N \boldsymbol{x}_{c_{1}}, \cdots, \boldsymbol{x}_{c_{m-1}}, \boldsymbol{x}_{1: N} xc1,⋯,xcm−1,x1:N 进行编码得到向量 e i \boldsymbol{e}_{i} ei ,则解码第 m m m 步时
a m = exp ( s m , n ) / Σ j = 1 N exp ( s m , j ) p ( c m ∣ c 1 : ( m − 1 ) , x 1 : N ) = a m (12) a_{}^{m}=\exp \left(s_{m, n}\right) / \Sigma_{j=1}^{N} \exp \left(s_{m,j}^{ }\right) \\ p\left(c_{m} \mid c_{1:(m-1)}, \boldsymbol{x}_{1: N}\right)= a_{}^{m}\tag{12} am=exp(sm,n)/Σj=1Nexp(sm,j)p(cm∣c1:(m−1),x1:N)=am(12)
其中 s m , n s_{m, n} sm,n 为在解码过程的第 m m m 步时 , h m , \boldsymbol{h}_{m} ,hm 对 e n \boldsymbol{e}_{n} en 的未归一化的注意力分布,即
s m , n = v ⊤ tanh ( W e n + U h m ) , ∀ n ∈ [ 1 , N ] (13) s_{m, n}=\boldsymbol{v}^{\top} \tanh \left(\boldsymbol{W} \boldsymbol{e}_{n}+\boldsymbol{U} \boldsymbol{h}_{m}\right), \forall n \in[1, N]\tag{13} sm,n=v⊤tanh(Wen+Uhm),∀n∈[1,N](13)
其中 e n e_n en 是encoder的在时间序列 n n n次的隐藏层输出, h m {h}_{m} hm 是decoder在时间序列m次的隐藏状态输出。 v , W , U \boldsymbol{v}, \boldsymbol{W}, \boldsymbol{U} v,W,U 为可学习的参数.
上面只是解码出一个位置输出对应的标签,当第 t t t步解码出所有标签时:
s j t = v T tanh ( W e n + U h j ) , n = 1 , . . . N a i t = exp ( s i t ) / Σ j = 1 N exp ( s j t ) p t = arg max ( a 1 t , … , a N t ) (14) \begin{array}{c} s_{j}^{t}=\mathrm{v}^{\mathrm{T}} \tanh \left(\boldsymbol{W} \boldsymbol{e}_{n}+\boldsymbol{U} \boldsymbol{h}_{j}\right), n =1,... N\\ a_{i}^{t}=\exp \left(s_{i}^{t}\right) / \Sigma_{j=1}^{N} \exp \left(s_{j}^{t}\right) \\ p^{t}=\arg \max \left(a_{1}^{t}, \ldots, a_{N}^{t}\right) \end{array}\tag{14} sjt=vTtanh(Wen+Uhj),n=1,...Nait=exp(sit)/Σj=1Nexp(sjt)pt=argmax(a1t,…,aNt)(14)
图2 给出了指针网络的示例, 其中 h 1 , h 2 , h 3 \boldsymbol{h}_{1}, \boldsymbol{h}_{2}, \boldsymbol{h}_{3} h1,h2,h3 为输入数字 20,5,10 经过循环 神经网络的隐状态 , h 0 , \boldsymbol{h}_{0} ,h0 对应一个特殊字符“<. 当输入 '>'时, 网络一步一步输出 三个输入数字从大到小排列的下标.
3、self-attention 模型
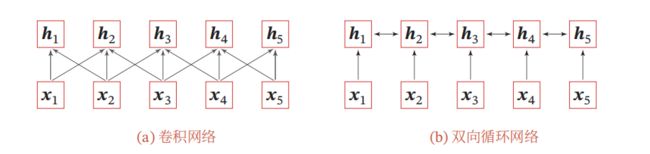
当使用神经网络来处理一个变长的向量序列时,我们通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列,如图3所示.
图 3 图3 图3
基于卷积或循环网络的序列编码都是一种局部的编码方式,只建模了输入信息的局部依赖关系.虽然循环网络理论上可以建立长距离依赖关系,但是由于信息传递的容量以及梯度消失问题,实际上也只能建立短距离依赖关系.
我们提到 CNN 和 RNN 在处理长序列时,都存在长距离依赖问题,那么你是否会有这样 几个问题:
- 长距离依赖问题 是什么呢?
- 为什么 CNN 和 RNN 无法解决长距离依赖问题?
- 之前提出过哪些解决方法?
- self-attention 是如何 解决 长距离依赖问题的呢?
长距离依赖问题 是什么呢?
- 介绍:对于序列问题,第 t t t 时刻 的 输出 y t y_t yt 依赖于 t t t 之前的输入,也就是 说 依赖于 x t − k , k = 1 , . . . , t x_{t-k}, k=1,...,t xt−k,k=1,...,t,当间隔 k k k 逐渐增大时, x t − k x_{t-k} xt−k 的信息将难以被 y t y_t yt 所学习到,也就是说,很难建立 这种 长距离依赖关系,这个也就是 长距离依赖问题(Long-Term Dependencies Problem)。
为什么 CNN 和 RNN 无法解决长距离依赖问题?
- CNN:
- 捕获信息的方式:
- CNN 主要采用卷积核的方式捕获句子内的局部信息,你可以把他理解为 基于 n-gram 的局部编码方式捕获局部信息
- 问题:
- 因为是 n-gram 的局部编码方式,那么当 k k k 距离 大于 n n n 时,那么 y t y_t yt 将难以学习 x t − k x_{t-k} xt−k 信息;
- 举例:
- 其实 n-gram 类似于人的视觉范围,人的视觉范围 在每一时刻只能捕获一定范围内 的信息,比如,你在看前面的时候,你是不可能注意到背后发生了什么,除非你转过身往后看。
- 捕获信息的方式:
- RNN:
- 捕获信息的方式:
- RNN 主要 通过 循环 的方式学习(记忆) 之前的信息 x t x_{t} xt;
- 问题:
- 但是随着时间 t t t 的推移,你会出现梯度消失或梯度爆炸问题,这种问题使你只能建立短距离依赖信息。
- 举例:
- RNN 的学习模式好比于人类 的记忆力,人类可能会对 短距离内发生的 事情特别清楚,但是随着时间的推移,人类开始 会对 好久之前所发生的事情变得印象模糊,比如,你对小时候发生的事情,印象模糊一样。
- 解决方法:
- 针对该问题,后期也提出了很多 RNN 变体,比如 LSTM、 GRU,这些变体 通过引入 门控的机制 来 有选择性 的记忆 一些 重要的信息,但是这种方法 也只能在 一定程度上缓解 长距离依赖问题,但是并不能 从根本上解决问题。
- 捕获信息的方式:
如果要建立输入序列之间的长距离依赖关系,可以使用以下两种方法:一种方法是增加网络的层数,通过一个深层网络来获取远距离的信息交互;另一种方法是使用全连接网络.全连接网络是一种非常直接的建模远距离依赖的模型,但是无法处理变长的输入序列.不同的输入长度,其连接权重的大小也是不同的.这时我们就可以利用注意力机制来“动态”地生成不同连接的权重,这就是自注意力模型(Self-Attention Model).
为了提高模型能力,自注意力模型经常采用查询-键-值(Query-Key-Value,QKV)模式,其计算过程如图4所示,其中红色字母表示矩阵的维度.
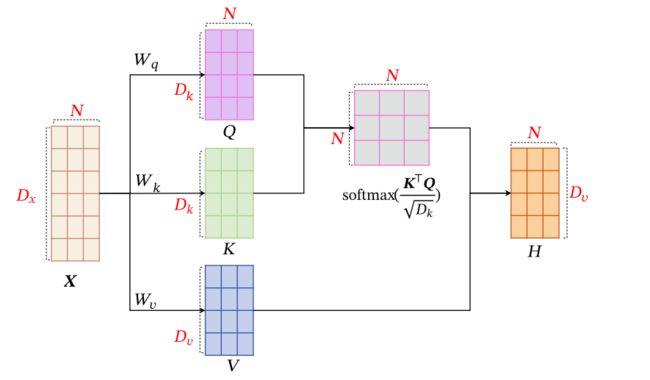
图 4 自 注 意 力 模 型 的 计 算 过 程 图4 自注意力模型的计算过程 图4自注意力模型的计算过程
计算注意力
#步骤1:准备输入
x = [
[1, 0, 1, 0], # Input 1
[0, 2, 0, 2], # Input 2
[1, 1, 1, 1] # Input 3
]
x = tf.constant(x, dtype=tf.float32)
#步骤2:初始化权重
w_key = [
[0, 0, 1],
[1, 1, 0],
[0, 1, 0],
[1, 1, 0]
]
w_query = [
[1, 0, 1],
[1, 0, 0],
[0, 0, 1],
[0, 1, 1]
]
w_value = [
[0, 2, 0],
[0, 3, 0],
[1, 0, 3],
[1, 1, 0]
]
w_key = tf.constant(w_key, dtype=tf.float32)
w_query = tf.constant(w_query, dtype=tf.float32)
w_value = tf.constant(w_value, dtype=tf.float32)
#步骤3:派生键,查询和值
keys = x @ w_key
querys = x @ w_query
values = x @ w_value
print(keys)
print(querys)
print(values)
#步骤4:计算注意力分数
attn_scores = tf.matmul(querys, keys, transpose_b=True)
print(attn_scores)
#步骤5: 缩放 matmul_q
dk = tf.cast(tf.shape(keys)[-1], tf.float32)
scaled_attention = attn_scores / tf.math.sqrt(dk)
print(scaled_attention)
#步骤6: 计算softmax
attn_scores_softmax = tf.nn.softmax(scaled_attention, axis=-1)
print(attn_scores_softmax)
#步骤7:将分数乘以值
weighted_values = tf.matmul(attn_scores_softmax, values)
print(weighted_values)
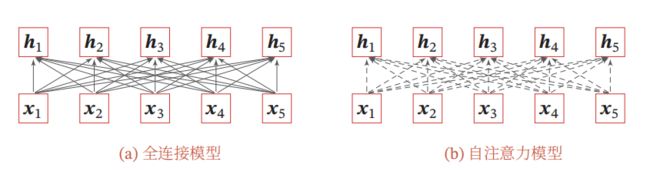
图5给出全连接模型和自注意力模型的对比,其中实线表示可学习的权重,虚线表示动态生成的权重.由于自注意力模型的权重是动态生成的,因此可以处理变长的信息序列.
图 5 全 连 接 模 型 和 自 注 意 力 模 型 图5 全连接模型和自注意力模型 图5全连接模型和自注意力模型
self-attention 是如何 解决 长距离依赖问题的呢?
-
解决方式:
- 利用注意力机制来“动态”地生成不同连接的权重,从而处理变长的信息序列
-
具体介绍:
- 对于 当前query,你需要与句子中所有 key 进行点乘后再 Softmax ,以获得句子中所有 key 对于 当前query 的 score(可以理解为贡献度),然后与 所有词 的 value 向量进行加权融合之后,就能使 当前 y t y_t yt 学习到句子中 其他词 x t − k x_{t-k} xt−k的信息;
-
举例
- 答案就是文章中的Q,K,V,这三个向量都可以表示"我"这个词,但每个向量的作用并不一样,Q 代表 query,当计算"我"这个词时,它就能代表"我"去和其他词的 K 进行点乘计算其他词对这个词的重要性,所以此时其他词(包括自己)使用 K 也就是 key 代表自己,当计算完点乘后,我们只是得到了每个词对“我”这个词的权重,需要再乘以一个其他词(包括自己)的向量,也就是V(value),才完成"我"这个词的计算,同时也是完成了用其他词来表征"我"的一个过程
-
优点
- 捕获源端和目标端词与词间的依赖关系
- 捕获源端或目标端自身词与词间的依赖关系
4、情感分类中的注意力
首先经 过 embedding 层得到 [ w 0 , w 1 , w 1 , ⋯ , w n ] , \left[w_{0}, w_{1}, w_{1}, \cdots, w_{n}\right], [w0,w1,w1,⋯,wn], 然后经过 B I L S T M \mathrm{BILSTM} BILSTM 把数 据 [ w 0 , w 1 , w 1 , ⋯ , w n ] \left[w_{0}, w_{1}, w_{1}, \cdots, w_{n}\right] [w0,w1,w1,⋯,wn]转换成另一种分布式向量表示,得到 [ h 0 , h 1 , h 2 , … , h n ] , \left[h_{0}, h_{1}, h_{2}, \ldots, h_{n}\right], [h0,h1,h2,…,hn], 公式如
下:
[ h 0 ; … ; h n ] = B I L S T M ( [ w 0 ; … ; w n ] ) (15) \left[h_{0} ; \ldots ; h_{n}\right]=B I L S T M\left(\left[w_{0} ; \ldots ; w_{n}\right]\right)\tag{15} [h0;…;hn]=BILSTM([w0;…;wn])(15)
target 用 h t h_{t} ht 表示, h t h_{t} ht 是 [ h t 0 ; … ; h t m ] \left[h_{t_{0}} ; \ldots ; h_{t_{m}}\right] [ht0;…;htm] 的平均值。 left_context 就是 [ h 0 , … , h t 0 − 1 ] \left[h_{0}, \ldots, h_{t_{0}-1}\right] [h0,…,ht0−1],right_context 就是 [ h t m + 1 , … , h n ] \left[h_{t_{m}+1}, \ldots, h_{n}\right] [htm+1,…,hn].
Vanilla Attention
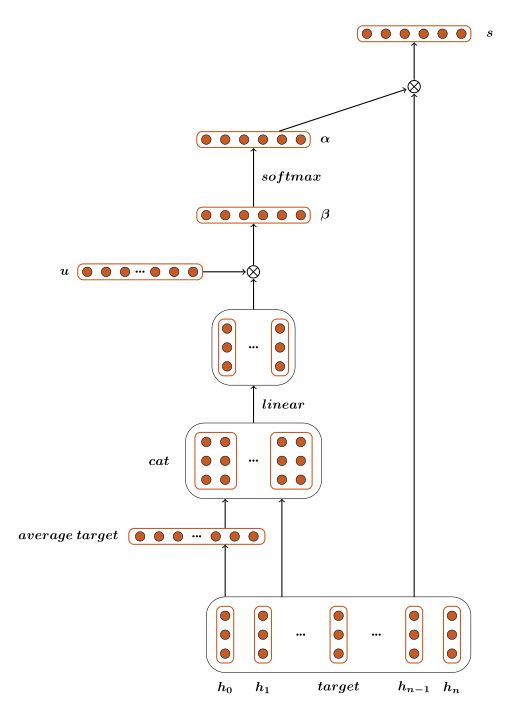
第一个attention模型是Vanilla attention model。首先通过计算每一个词的权重 α ( α \alpha(\alpha α(α 是一个标量),与每一个词的向量表示相乘后再求和, 最后得到整句话 s \mathrm{s} s 的向量表示:
s = attention ( [ h 0 ; … ; h n ] , h t ) = ∑ i n α i ⋅ h i (16) s=\operatorname{attention}\left(\left[h_{0} ; \ldots ; h_{n}\right], h_{t}\right)=\sum_{i}^{n} \alpha_{i} \cdot h_{i}\tag{16} s=attention([h0;…;hn],ht)=i∑nαi⋅hi(16)
求 α \alpha α的公式:
α i = exp ( β i ) ∑ j n exp ( β j ) (17) \alpha_{i}=\frac{\exp \left(\beta_{i}\right)}{\sum_{j}^{n} \exp \left(\beta_{j}\right)}\tag{17} αi=∑jnexp(βj)exp(βi)(17)
β \beta β的值是由target和上下文单词共同决定的。从下面公式可以看出,每个词与target相连 接,经过一个线性层与 tanh \tanh tanh 激活函数,然后与张量 U U U相乘得到一个标量。公式如下:
β i = U T tanh ( W 1 ⋅ [ h i , h t ] + b 1 ) (18) \beta_{i}=U^{T} \tanh \left(W_{1} \cdot\left[h_{i}, h_{t}\right]+b_{1}\right)\tag{18} βi=UTtanh(W1⋅[hi,ht]+b1)(18)
通过以上公式, 能求得该句子的最后表示 s , s, s, 然后用 s s s 来预测情感标签可能的分布 p,最后经过一个线性层和一个softmax激活函数得到预测值 p p p 。求 p p p 公式如下:
p = softmax ( W 2 ⋅ s + b 2 ) (19) p=\operatorname{softmax}\left(W_{2} \cdot s+b_{2}\right)\tag{19} p=softmax(W2⋅s+b2)(19)
模型流程图如下:
Contextualized Attention
Contextualized Attention Model是在Vanilla Model的基础上衍生的一个模型。这个 模型将上下文拆分成两部分,分别为 left_context 和 right_context 。然后对 left_context 和 right_context 分别做与Vanilla Attention Model一样的操作。即:
s = attention ( [ h 0 ; … h n ] , h t ) s l = attention ( [ h 0 ; … h t 0 − 1 ] , h t ) s r = attention ( [ h t m + 1 ; … h n ] , h t ) (20) \begin{aligned} s &=\operatorname{attention}\left(\left[h_{0} ; \ldots h_{n}\right], h_{t}\right) \\ s_{l} &=\text { attention }\left(\left[h_{0} ; \ldots h_{t_{0}-1}\right], h_{t}\right) \\ s_{r} &=\text { attention }\left(\left[h_{t_{m}+1} ; \ldots h_{n}\right], h_{t}\right) \end{aligned}\tag{20} sslsr=attention([h0;…hn],ht)= attention ([h0;…ht0−1],ht)= attention ([htm+1;…hn],ht)(20)
这三个向量经过线性层的和, 再经过 softmax,,得到预测值 p p p 。公式如下:
p = softmax ( W 1 ⋅ s + W l ⋅ s l + W r ⋅ s r + b 1 ) (21) p=\operatorname{softmax}\left(W_{1} \cdot s+W_{l} \cdot s_{l}+W_{r} \cdot s_{r}+b_{1}\right)\tag{21} p=softmax(W1⋅s+Wl⋅sl+Wr⋅sr+b1)(21)
Contextualized Attention with Gates
受到LSTM中 gate 的启发,拼弃了Contextualized Attention中直接过线性层的 方法, 采取了 gate 的方法。考虑到代表情感的特征可以在左边语境 (left_context) 中 或者右边的语境 (right_context) 中,于是采用了 gate 的方法控制 s , s l , s r s, s_{l}, s_{r} s,sl,sr 这三个数 据流的流出。这三个 gate 分别是 z , z l , z r , z, z_{l}, z_{r}, z,zl,zr, 公式如下:
z ∝ exp ( W 1 ⋅ s + U 1 ⋅ h t + b 1 ) z r ∝ exp ( W 3 ⋅ s r + U 3 ⋅ h t + b 3 ) z l ∝ exp ( W 2 ⋅ s l + U 2 ⋅ h t + b 2 ) (22) \begin{aligned} z & \propto \exp \left(W_{1} \cdot s+U_{1} \cdot h_{t}+b_{1}\right) \\ z_{r} & \propto \exp \left(W_{3} \cdot s_{r}+U_{3} \cdot h_{t}+b_{3}\right) \\ z_{l} & \propto \exp \left(W_{2} \cdot s_{l}+U_{2} \cdot h_{t}+b_{2}\right) \end{aligned}\tag{22} zzrzl∝exp(W1⋅s+U1⋅ht+b1)∝exp(W3⋅sr+U3⋅ht+b3)∝exp(W2⋅sl+U2⋅ht+b2)(22)
并且 z , z l , z r z, z_{l}, z_{r} z,zl,zr 要满足 z + z l + z r = 1 → , z+z_{l}+z_{r}=\overrightarrow{1}, z+zl+zr=1, 即三个向量的和为1向量。
接下来 gate 与数据流按位相乘得到最后的向量表示:
s ~ = z ⊙ s + z l ⊙ s l + z r ⊙ s r (23) \tilde{s}=z \odot s+z_{l} \odot s_{l}+z_{r} \odot s_{r}\tag{23} s~=z⊙s+zl⊙sl+zr⊙sr(23)
最后经过一个线性层和 softmax 得到预测值 p : \mathrm{p}: p:
p = softmax ( W 4 ⋅ s ~ + b 4 ) (242) p=\operatorname{softmax}\left(W_{4} \cdot \tilde{s}+b_{4}\right)\tag{242} p=softmax(W4⋅s~+b4)(242)
具体代码详解: Vanilla Model不用把句子分割成left_context和right_context。因此很容易实现batch_size > 1的设计。主要的层次有embedding层,dropout层,双向lstm层,线性层linear_2。linear_1层和参数u主要是为了计算的。
class Vanilla(nn.Module):
def __init__(self, embedding):
super(Vanilla, self).__init__()
self.embedding = nn.Embedding(embed_num, embed_dim)
self.embedding.weight.data.copy_(embedding)
self.dropout = nn.Dropout(dropout)
self.bilstm = nn.LSTM(embed_dim,hidden_size,dropout)
self.linear_1 = nn.Linear(hidden_size,attention_size,bias=True)
self.u = Parameter(torch.randn(1,attention_size),
self.linear_2 = nn.Linear(hidden_size,label_num,bias=True)
def forward():
pass
Attention C和Attention -G模型需要把句子分割成left_context和right_context。编程上很难设计出很好的batch_size > 1的方法,因此使用的是batch_size = 1的方法。这两个模型是Vanilla Model的衍生,所以在代码上有所依赖,因此设计了一个Attention Class,作用是为了计算s。这个类是计算图的一部分,输入是context和target,输出是s。
class Attention(nn.Module):
def __init__(self):
super(Attention, self).__init__()
self.linear = nn.Linear(input_size * 2, output_size, bias=True)
self.u = Parameter(torch.randn(output_size, 1)) def forward():
pass
Attention -C模型会用到Attention类。 Attention -G模型中的操作,使用softmax函数实现该操作。
# cat z_all, z_l, z_r
z_all = torch.cat([z_all, z_l, z_r], 1)
# softmax
z_all = F.softmax(z_all)
详细代码参考代码在github上:
https://github.com/vipzgy/AttentionTargetSentiment
5、seq2seq Attention
从输出端,即decoder部分,倒过来一步一步看公式。
S t = f ( S t − 1 , y t − 1 , c t ) (1) S_t=f(S_{t-1}, y_{t-1}, c_t) \tag{1} St=f(St−1,yt−1,ct)(1)
St是指decoder在t时刻的状态输出,St−1是指decoder在t−1时刻的状态输出,yt−1是t−1时刻的label(注意是label,不是我们输出的y),ct看下一个公式,f是一个RNN。
c t = ∑ j = 1 T x a t j h j (2) {c_{t}} = \sum\limits_{j = 1}^{ {T_x}} { {a_{tj}}{h_j}} \tag{2} ct=j=1∑Txatjhj(2)
hj是指第j个输入在encoder里的输出,atj是一个权重
a t j = e x p ( e t j ) ∑ k = 1 T x e x p ( e t k ) (3) {a_{tj}} = \frac{ {exp \left( { {e_{tj}}} \right)}}{ {\sum\nolimits_{k = 1}^{ {T_x}} {exp \left( { {e_{tk}}} \right)} }} \tag{3} atj=∑k=1Txexp(etk)exp(etj)(3)
这个公式跟softmax是何其相似,道理是一样的,是为了得到条件概率P(a|e),这个a的意义是当前这一步decoder对齐第j个输入的程度。
最后一个公式,
e t j = g ( S t − 1 , h j ) = V ⋅ tanh ( W ⋅ h j + U ⋅ S t − 1 + b ) (4) e_{tj} = g(S_{t-1}, h_j) = V\cdot \tanh { \left( W\cdot h_j+U\cdot S_{t-1}+b \right) } \tag{4} etj=g(St−1,hj)=V⋅tanh(W⋅hj+U⋅St−1+b)(4)
这个g可以用一个小型的神经网络来逼近,它用来计算St−1, hj这两者的关系分数,如果分数大则说明关注度较高,注意力分布就会更加集中在这个输入单词上.
参考
《神经网络与深度学习》 邱锡鹏
注意力机制
详解深度学习中“注意力机制”
Self-Attention Generative Adversarial Networks.
https://arxiv.org/pdf/1706.03762.pdf
A simple neural attentive meta-learner
推荐系统中的注意力机制https://zhuanlan.zhihu.com/p/51623339