深度学习激活函数Activation Function汇总：sigmoid、tanh、ReLU、Leaky ReLU、ELU、Swish、Mish

————————————————————————
文中激活函数及其导数的绘制，请参考： python绘制激活函数及其导数图像
————————————————————————

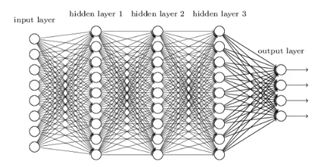
什么是激活函数？
——激活函数Activation Function：在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。
为什么要用激活函数？
——激活函数可增加模型的非线性，没有激活函数，无论你的神经网络有多少层，输入和输出都是线性组合，每层相当于矩阵相乘，叠加了N层之后也是矩阵相乘。
说起激活函数，大家很常看到的两个词“梯度消失”和“梯度爆炸”，那么，什么是“梯度消失”和“梯度爆炸”呢？

1.sigmoid

sigmoid函数也叫Logistic函数，表达式及其导数如下：

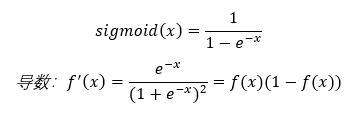
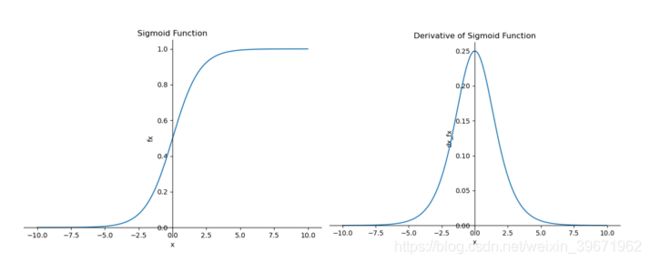
特点：经过sigmoid函数后，输出值变换为[0,1]，对于大的负数输出为0，大的正数输出为1。由下图左可以看出，Sigmoid函数在（-∞，5）部分输出为0，在（5，+∞）部分输出为1。
优点：sigmoid函数平滑，函数简单容易求导
缺点：
1、容易出现梯度消失。由下图右可以看出，sigmoid的导数取值范围为[0,0.25]，如果初始化权值在（0，1）之间，由神经网络反向传播时的链式法则，梯度反向传播时，激活函数偏导逐层相乘，因此，当神经网络的隐含层特别多时，梯度逐层乘以小于1的数导致最终趋于0，即出现梯度消失。当网络权值初始化为(1,+∞)时，则会出现梯度爆炸情况。
2、计算量大。在正向传播和反向传播中都包含幂运算和除法，导致计算量增大。
3、Sigmoid的输出不是0均值zero-centered：由下图左可以看出，Sigmoid函数的输出的均值全为正，而并非为0，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布。

2.Tanh

Tanh为双曲正切函数，表达式为：

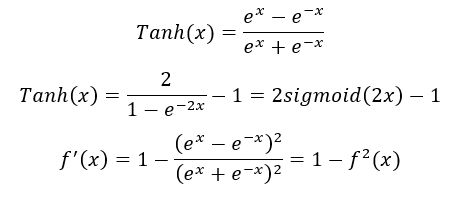
特点：经过tanh函数后，输出值变换为[-1,1]。tanh实际上是sigmoid函数变化而来的，由下图左可以看出，tanh是sigmoid经过平移和拉伸得来的，这解决了sigmoid的0均值zero-centered问题。
优点：解决了sigmoid的0均值zero-centered问题
缺点：
1、梯度消失：由图右可以看出，tanh的导数取值范围为[0,1]，相比于sigmoid的[0,0.25]，虽然梯度消失现象有所缓解，但仍然存在。
2、计算量大：幂运算和除法仍然存在。

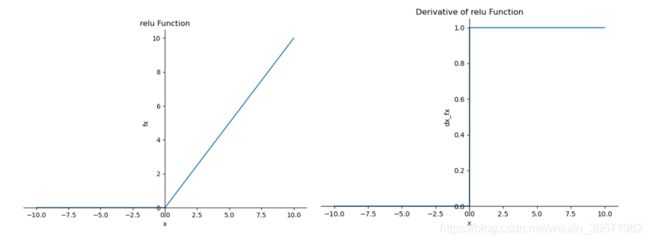
3.ReLU

修正线性单元（Rectified Linear Unit, ReLU），表达式为：

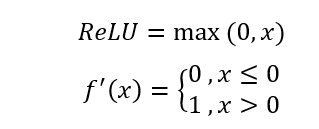
特点：ReLU简单，没有了sigmoid和tanh的指数运算，实际就是取最大值函数。
ReLU在x>0下，导数为常数1的特点：由右图可以看出，在x>0的时候，ReLU的导数为常数1，这样可以避免梯度消失现象，但梯度下降的强度就完全取决于权值的乘积，那么，这样就可能会出现梯度爆炸问题。解决这类梯度爆炸的问题：一是控制权值，让它们在（0，1）范围内；二是做梯度裁剪，控制梯度下降强度，如ReLU(x)=min(6, max(0,x))。
ReLU在x<0下，输出置为0的特点：深度学习是根据大批量样本数据，从错综复杂的数据关系中，找到关键信息（关键特征）。换句话说，就是把密集矩阵转化为稀疏矩阵，保留数据的关键信息，去除噪音，这样的模型就有了鲁棒性。ReLU将x<0的输出置为0，就是一个去噪音，稀疏矩阵的过程。而且在训练过程中，这种稀疏性是动态调节的，网络会自动调整稀疏比例，保证矩阵有最优的有效特征。但是，但是ReLU 强制将x<0部分的输出置为0（置为0就是屏蔽该特征），可能会导致模型无法学习到有效特征，所以如果学习率设置的太大，就可能会导致网络的大部分神经元处于‘dead’状态，所以使用ReLU的网络，学习率learning rate不能设置太大。
优点：
1、解决了sigmoid和tanh函数梯度消失的问题；
2、相较于sigmoid和tanh函数的指数运算，ReLU计算更快；
3、ReLU收敛速度比sigmoid和tanh函数约快6倍左右。
缺点：
1、ReLU输出不是0均值zero-centered；
2、ReLU的死区问题：由下图右可看出，x<0时，梯度为0，此时参数不能被更新，导致网络处于死区状态。使用ReLU的网络，学习率learning rate不能设置太大。

4.Leaky ReLU

Leaky ReLU的表达式为：

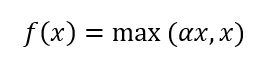
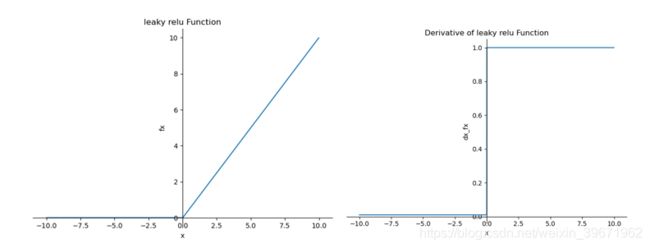
为了解决ReLU死区现象，提出Leaky ReLU。当x<0时，输出为αx，而不是0，通常α为比较小的正数0.01或者0.001。由于Leaky ReLU中的α为超参数，比较难设定合适的值，在实际的使用过程中，Leaky ReLU的性能并没有说总比ReLU好。

5.ELU

指数线性单元（Exponential Linear Units，ELU），


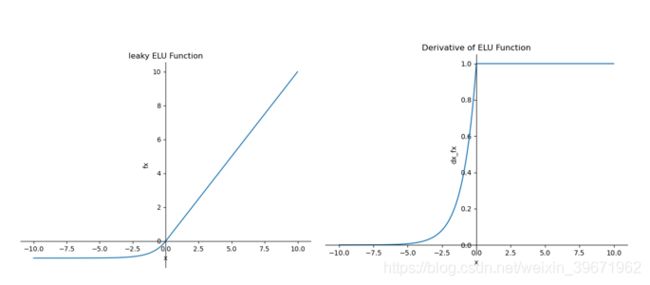
特点：ELU具备了ReLU的优点，解决了ReLU的死区现象，ELU输出均值接近0，但是ELU中含有指数操作，计算量也相应增加。通常，ELU的超参数α=1。
优点：
（1）ELU具备了ReLU的优点：解决了sigmoid和tanh函数梯度消失的问题；相较于sigmoid和tanh函数的指数运算，ReLU计算更快；ReLU收敛速度比sigmoid和tanh函数约快6倍左右。
（2）解决了ReLU的死区现象
（3）ELU输出均值接近0
缺点：ELU中含有指数操作，计算量增加

6.Swish

swish来源于论文“SEARCHING FOR ACTIVATION FUNCTIONS”



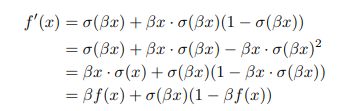
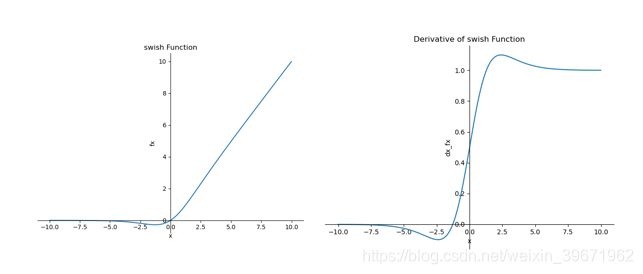
特点：Swish 具备无上界有下界、平滑、非单调的特性。
优点：ReLU有无上界和有下界的特点，而Swish相比ReLU又增加了平滑和非单调的特点，这使得其在ImageNet上的效果更好。
缺点：引入了指数函数，增加了计算量

7.Mish

Mish来源于论文：Mish: A Self Regularized Non-Monotonic Activation Function



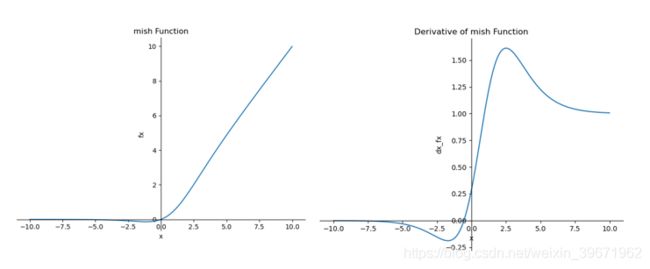
特点：无上界(unbounded above)、有下界(bounded below)、平滑(smooth)和非单调(nonmonotonic)。
无上界：可以防止网络饱和，即梯度消失。
有下界：提升网络的正则化效果。
平滑：首先在0值点连续相比ReLU可以减少一些不可预料的问题，其次可以使网络更容易优化并且提高泛化性能。
非单调：可以使一些小的负输入也被保留为负输出，提高网络的可解释能力和梯度流
优点：平滑、非单调、上无界、有下界
缺点：引入了指数函数，增加了计算量

激活函数使用小Tips:
1、除非输出层是二分类问题，尽量不要使用sigmoid函数；
2、tanh函数几乎适合所有的场景
3、最常用的激活函数是ReLU，不确定用哪个激活函数就用ReLU试试看

参考：
1、激活函数总结；
2、深度学习中几种常见的激活函数理解与总结
3、Mish: A Self Regularized Non-Monotonic Neural Activation Function论文笔记
4、详解机器学习中的梯度消失、爆炸原因及其解决方法