MatConvNet之softmaxloss原理及其代码实现
在卷积神经网络ConvNets中,前向传播到最后一层计算网络预测标签(predicted label)与真实标签(Ground Truth)之间的误差,需要定义一个损失函数,如Log loss,Softmax log loss,Multiclass hinge loss,Multiclass structured hinge loss等,本文要讲的就是Softmax log loss损失函数在ConvNets前向及反向传播中原理及其代码实现。
1. softmaxloss原理
首先看一下softmax函数,因为在接下来定义softmaxloss损失函数涉及到softmax。说一些题外话,这里的'soft'是相对'hard'而言的,其中'hard assignment'就是'硬赋值',就比如这里的取最大值,如果采用'hard assignment', c=max(a,b),则c只能取a或b,函数表示的话就会在a或b处出现断点,导致函数不可微,那么在ConvNets中就无法实现反向传播。所以要对其进行改造,也就有了'soft assignment',这里就需要设计一个函数,并且是单调递增的,这样才能保持大值经过函数映射后仍为较大的值,同时考虑到求导的方便性,于是就想到了指数函数softmax。
softmax原理及相关求导:
参考来源:详解softmax函数以及相关求导过程
当我们对分类的Loss进行改进的时候,我们要通过梯度下降,每次优化一个step大小的梯度,这个时候我们就要求Loss对每个权重矩阵的偏导,然后应用链式法则。那么这个过程的第一步,就是对softmax求导传回去,不用着急,我后面会举例子非常详细的说明。在这个过程中,你会发现用了softmax函数之后,梯度求导过程非常非常方便!
下面我们举出一个简单例子,原理一样,目的是为了帮助大家容易理解!

我们能得到下面公式:
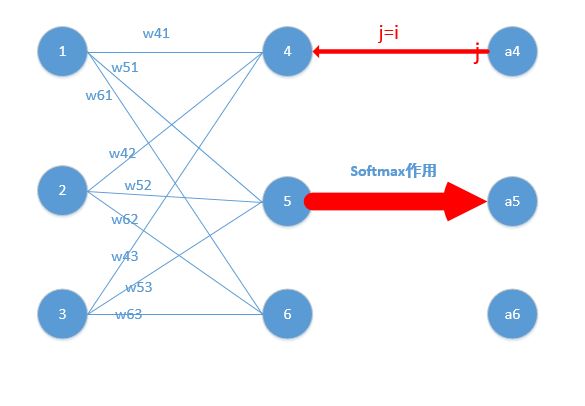
z4 = w41*o1+w42*o2+w43*o3
z5 = w51*o1+w52*o2+w53*o3
z6 = w61*o1+w62*o2+w63*o3
z4,z5,z6分别代表结点4,5,6的输出,01,02,03代表是结点1,2,3往后传的输入.
那么我们可以经过softmax函数得到
现在看起来是不是感觉复杂了,居然还有累和,然后还要求导,每一个a都是softmax之后的形式!
但是实际上不是这样的,我们往往在真实中,如果只预测一个结果,那么在目标中只有一个结点的值为1,比如我认为在该状态下,我想要输出的是第四个动作(第四个结点),那么训练数据的输出就是a4 = 1,a5=0,a6=0,哎呀,这太好了,除了一个为1,其它都是0,那么所谓的求和符合,就是一个幌子,我可以去掉啦!
为了形式化说明,我这里认为训练数据的真实输出为第j个为1,其它均为0!
针对上述论断,有一个小知识点需要补充说明:
参考来源:Softmax回归
所以才有“但是实际上不是这样的,我们往往在真实中,如果只预测一个结果,那么在目标中只有一个结点的值为1,比如我认为在该状态下,我想要输出的是第四个动作(第四个结点),那么训练数据的输出就是a4 = 1,a5=0,a6=0,哎呀,这太好了,除了一个为1,其它都是0,那么所谓的求和符合,就是一个幌子,我可以去掉啦!”
接上文:
参数的形式在该例子中,总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些,那么比如我要求出w41,w42,w43的偏导,就需要将Loss函数求偏导传到结点4,然后再利用链式法则继续求导即可,举个例子此时求w41的偏导为:

w51.....w63等参数的偏导同理可以求出,那么我们的关键就在于Loss函数对于结点4,5,6的偏导怎么求,如下:
这里分为俩种情况:
 j=i对应例子里就是如下图所示:
j=i对应例子里就是如下图所示:
比如我选定了j为4,那么就是说我现在求导传到4结点这!
 那么由上面求导结果再乘以交叉熵损失函数求导
那么由上面求导结果再乘以交叉熵损失函数求导
第二种情况为:

这里对应我的例子图如下,我这时对的是j不等于i,往前传:

那么由上面求导结果再乘以交叉熵损失函数求导
以上是关于softmax原理及相关求导完结,下面开始讲解softmaxloss的原理及求导:
参考来源:Caffe Softmax层的实现原理?
一定要熟悉这里的softmaxloss原理及推导,方便理解后边将要提到的代码实现问题。其实在计算softmax归一化概率时,还有一个预处理步骤,后文的代码实现也是按照这个处理取实现的:
参考来源:caffe层解读系列-softmax_loss
上文的第一步计算softmax归一化概率还涉及到一个小知识点:
参考来源:Softmax回归
至此关于softmaxloss原理部分至此完结,下面开始讲解关于softmaxloss的代码实现,该实现是基于深度学习库MatConvNet框架的实现,代码如下:
function y = vl_nnsoftmaxloss(x,c,dzdy)
%VL_NNSOFTMAXLOSS CNN combined softmax and logistic loss.
% **Deprecated: use `vl_nnloss` instead**
%
% Y = VL_NNSOFTMAX(X, C) applies the softmax operator followed by
% the logistic loss the data X. X has dimension H x W x D x N,
% packing N arrays of W x H D-dimensional vectors.
%
% C contains the class labels, which should be integers in the range
% 1 to D. C can be an array with either N elements or with dimensions
% H x W x 1 x N dimensions. In the fist case, a given class label is
% applied at all spatial locations; in the second case, different
% class labels can be specified for different locations.
%
% DZDX = VL_NNSOFTMAXLOSS(X, C, DZDY) computes the derivative of the
% block projected onto DZDY. DZDX and DZDY have the same dimensions
% as X and Y respectively.
% Copyright (C) 2014-15 Andrea Vedaldi.
% All rights reserved.
%
% This file is part of the VLFeat library and is made available under
% the terms of the BSD license (see the COPYING file).
% work around a bug in MATLAB, where native cast() would slow
% progressively
if isa(x, 'gpuArray')
switch classUnderlying(x) ;
case 'single', cast = @(z) single(z) ;
case 'double', cast = @(z) double(z) ;
end
else
switch class(x)
case 'single', cast = @(z) single(z) ;
case 'double', cast = @(z) double(z) ;
end
end
%X = X + 1e-6 ;
sz = [size(x,1) size(x,2) size(x,3) size(x,4)] ;
if numel(c) == sz(4)
% one label per image
c = reshape(c, [1 1 1 sz(4)]) ;
end
if size(c,1) == 1 & size(c,2) == 1
c = repmat(c, [sz(1) sz(2)]) ;
end
% one label per spatial location
sz_ = [size(c,1) size(c,2) size(c,3) size(c,4)] ;
assert(isequal(sz_, [sz(1) sz(2) sz_(3) sz(4)])) ;
assert(sz_(3)==1 | sz_(3)==2) ;
% class c = 0 skips a spatial location
mass = cast(c(:,:,1,:) > 0) ;
if sz_(3) == 2
% the second channel of c (if present) is used as weights
mass = mass .* c(:,:,2,:) ;
c(:,:,2,:) = [] ;
end
% convert to indexes
c = c - 1 ;
c_ = 0:numel(c)-1 ;
c_ = 1 + ...
mod(c_, sz(1)*sz(2)) + ...
(sz(1)*sz(2)) * max(c(:), 0)' + ...
(sz(1)*sz(2)*sz(3)) * floor(c_/(sz(1)*sz(2))) ;
% compute softmaxloss
xmax = max(x,[],3) ;
ex = exp(bsxfun(@minus, x, xmax)) ;
%n = sz(1)*sz(2) ;
if nargin <= 2
t = xmax + log(sum(ex,3)) - reshape(x(c_), [sz(1:2) 1 sz(4)]) ;
y = sum(sum(sum(mass .* t,1),2),4) ;
else
y = bsxfun(@rdivide, ex, sum(ex,3)) ;
y(c_) = y(c_) - 1;
y = bsxfun(@times, y, bsxfun(@times, mass, dzdy)) ;
end在ConvNets前向传播时,函数y = vl_nnsoftmaxloss(x,c,dzdy)仅有两个输入参数,也就是第三个参数dzdy被忽略,在代码中的体现为:
if nargin <= 2
t = xmax + log(sum(ex,3)) - reshape(x(c_), [sz(1:2) 1 sz(4)]) ;
y = sum(sum(sum(mass .* t,1),2),4) ;也就是函数vl_nnsoftmaxloss只有两个输入参数时计算一个batchSize的总的损失Loss。计算softmaxloss的代码如下:
% compute softmaxloss
xmax = max(x,[],3) ;
ex = exp(bsxfun(@minus, x, xmax)) ;下面重点理解代码,其就是按照"softmax_loss的计算包含2步"之计算损失实现的,只是把对数展开,这里的对数log就是指自然对数ln(在matlab中函数log()指自然对数计算),只是把这个对数展开,变为下式的代码实现:
t = xmax + log(sum(ex,3)) - reshape(x(c_), [sz(1:2) 1 sz(4)]) ;% convert to indexes
c = c - 1 ;
c_ = 0:numel(c)-1 ;
c_ = 1 + ...
mod(c_, sz(1)*sz(2)) + ...
(sz(1)*sz(2)) * max(c(:), 0)' + ...
(sz(1)*sz(2)*sz(3)) * floor(c_/(sz(1)*sz(2))) ;opts.lite = true ;
下面讲解ConvNets反向传播计算softmaxloss梯度的代码:
y = bsxfun(@rdivide, ex, sum(ex,3)) ;
y(c_) = y(c_) - 1;
y = bsxfun(@times, y, bsxfun(@times, mass, dzdy)) ; y(c_) = y(c_) - 1;% compute softmaxloss
xmax = max(x,[],3) ;
ex = exp(bsxfun(@minus, x, xmax)) ;
%n = sz(1)*sz(2) ;
if nargin <= 2
t = xmax + log(sum(ex,3)) - reshape(x(c_), [sz(1:2) 1 sz(4)]) ;
y = sum(sum(sum(mass .* t,1),2),4) ;
else
y = bsxfun(@rdivide, ex, sum(ex,3)) ;
y(c_) = y(c_) - 1;
y = bsxfun(@times, y, bsxfun(@times, mass, dzdy)) ;
end
function y = vl_nnloss(x,c,varargin)function res = vl_simplenn(net, x, dzdy, res, varargin)
参考来源:
1. 详解softmax函数以及相关求导过程
2. Softmax 函数的特点和作用是什么?
3. Caffe Softmax层的实现原理?
4. Softmax回归
5. caffe层解读系列-softmax_loss
6. 如何理解神经网络里面的反向传播算法?
7. 如何直观地解释 back propagation 算法?
8. A Step by Step Backpropagation Example
9. Convolutional Neural Networks (CNNs / ConvNets)
10. SVM, Softmax损失函数