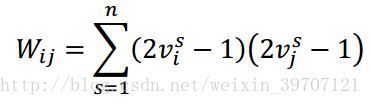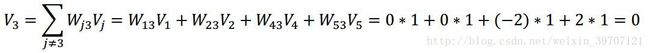离散型Hopdield神经网络联想记忆功能

Hopdield神经网络用于联想记忆介绍：

       如上图这个例子，这就是离散型Hopfield网络用于联想记忆的工作方式。我们以T这个字母为例，首先生成一张完整的T字形图片，然后将图片映射到神经网络中的每个神经元，即每个像素都对应网络中的一个神经元，T字上的像素映射到网络上的神经元，对应值是1（激活状态），T字外的像素映射到网络上的神经元，对应值为0（抑制状态）。然后进行训练，训练的过程是保持神经元状态不变，通过修改权值，使得当神经元的状态和T字形正好对应的同时，网络的能量函数

      正好到达最低点。训练完成后，网络便存储T这个模式。这样，如果在网络中再输入右图这种加入噪声、只有一半的T字图片（输入过程还是和训练一样，将像素点映射到神经元上），经过网络迭代，不断修改神经元的状态，能量函数到达训练时的最低点时，神经元的状态最终便会变成完整的T字形。训练过程实际就是：由于能量函数是有界的，所以系统最后必趋于稳定状态，并对应于在状态空间的某一局部极小值。适当地选取初始状态，网络状态最终将演化到初始状态附近的极小值。如果存储的模式正好对应于该极小值，则意味着当输入与存储样本相似时，会联想起极小值处的储存样本，所以Hopfield神经网络具有联想记忆功能。

过程理解：

       Hopfield网络中的每一个神经元既是输入也是输出，并且神经元之间是全连接的。这就是，每个神经元是网络中其他所有神经元的输入。所有神经云都是相互的输入，也是输出。正如上面所说，网络在计算中的作用是将一个扭曲的模式映射在网络的神经元上，迭代后最终停止在训练收敛时得到的极小值的模式之一。所以，需要知道的是：（1）如何训练网络（2）如何更新神经元（3）神经元的更新顺序如何得到（4）如何知道停留在了训练好的模式之一。

       如何训练网络：在Hopfield发表的论文中，他提供了一个公式，可以在没有任何训练的情况下计算权重值，使用 来表示神经元之间的权重。

假如想要存储一组模式 。设定权重公式为：

同时，

注意如果只存储一种模式，上式可以化简为：

       例如，我们使用5节点网络去识别模式(0 1 1 1 0)。那么需要一个5x5的权重矩阵，同时由于神经元的自权重都设置为0，所以权重矩阵对角线为0，矩阵如下所示：

从公式中可以得到：

因为权重是对称的，我们只用计算矩阵对角线上方的权重。V是待存储的模式，用向量（0 1 1 0 1）表示，所以 。权重矩阵计算如下：

这样得到权重矩阵：

现在来看看用5节点网络来存储 和两种模式。例如 按如下方法计算：

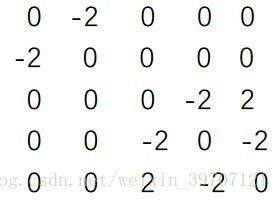
       或者可以先计算出第一种模式的权重矩阵，接着计算出第二种模式的权重矩阵，然后将这两种模式相加起来，最终得到如下矩阵：

       如何更新神经元：现在有了(0 1 1 0 1)和(1 0 1 0 1)两种模式的权重矩阵。一个要注意的问题是如果这两个模式只相差2位，把它们合在一起可能很难区分开来。通过类推，如果将小写“c”从“e”或大写“O”与“Q”区分开来，可能会遇到困难。更新Hopfield网络中的神经元非常像更新感知器。例如如果更新Hopfield网络的神经元3，则可以将感知器看作是感知器，将所有其他神经元的值作为输入值，将这些神经元到神经元3的权值作为权重。换句话说，首先对其他神经元的输入进行加权求和，如果该值大于或等于0，则输出1。否则，输出0。公式如下：

如果 ，则给它重赋值为1，否则赋值为0。

使用(0 1 1 0 1)和(1 0 1 0 1)的权重矩阵，计算神经元3的值：

       因为等于0，所以 重赋值1。在这种情况下， 的值不会改变。值得注意的是，由于从神经元3到自身的权重为0，我们可以计算权重矩阵中第3列的点积和当前状态来计算加权和：

       确定神经元更新顺序：你可能已经注意到在Hopfield网络中神经元的更新顺序问题有点棘手。如果它的输入值正在改变，你怎么能更新一个神经元呢？那么有两种方法。首先是同步更新，这意味着基于现有状态（即不是节点正在改变的值），所有节点同时被更新。要更新此方法中的节点，只需将权重矩阵乘以当前状态的向量即可。

       这在神经意义上不太现实，因为神经元并不全都以相同的速率更新。它们具有不同的传播延迟等问题，所以更现实的方法是以随机顺序更新它们。事实上，这是Hopfield所描述的方法。随机选择一个神经元并更新它，然后再随机选择另一个神经元并更新它。一直这样更新直到系统处于稳定状态。

       事实上，一般以半随机的顺序来更新Hopfield网络神经元。一次性更新所有的神经元，但是在这次总体更新中，神经元是以随机顺序更新的。所以可能的更新顺序是3,2,1,5,4,2,3,1,5,4等等，如果是纯粹是随机的，可能会出现3,2,1,2,2,2,5,1,2,2,4,2,1这种情况，所以这种措施是为了避免一个随机发生器不断更新某个神经元而不更新其他神经元。

       如何知道停留在了训练好的模式之一：如果更新一次网络后发现没有神经元继续变化，就表示网络已经收敛，可以停止更新状态了。 权值只在训练过程改变，训练完成后只有神经元的状态会发生改变。并且对于某一神经元，和它连接的神经元处于激活状态的越多，这个神经元也就越容易被激活。

能量函数：

Lyapunov函数保证了在模式回忆中能量函数的值可以不断下降，最终停在网络吸引子，神经网络达到一个稳定状态。

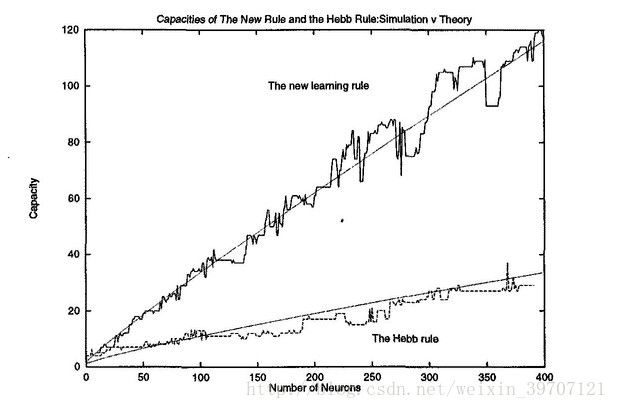
       这样Hopfiel网络便总能达到一个存储的模式，但是问题是达到的极小值并不一定是与输入相对应的正确的极小值，输出错误的结果。Hopfield神经网络可以存储的模式存在限制，下图是关于神经网络规模图和神经网络可以记忆的模式数量的关系图：

       Hopfield神经网络可以存储的模式数量和神经元数量也是有限制的，一般来说，模式数量和神经元数量之比应当在0.138之下，在这个比值之下，我们可以使用Hebbian学习算法来进行训练。

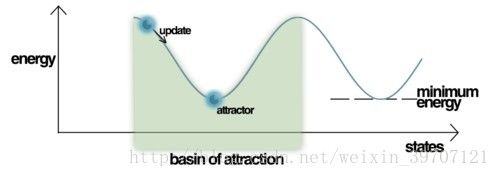
       我们需要储存另外一张图片的时候，我们只需要得到另外一个权值矩阵，然后把这两个矩阵相加就可以了。一个不太恰当的理解是在整个 Hopfield Network的状态空间里，我们可以用这种权值相加的方式人为的构造两个能量函数上的局部极小值，如下图所示：

       图中左边是第一个状态空间的局部极小值，右边是第二个状态空间上的局部极小值。当我们向网络输入一个靠近第二个局部极小值所在位置的向量的之后，在经过数次迭代，最终可以收敛于第二个局部极小值。这就是Hopfield神经网络可以通过一个不完整的信息得到完整信息的原理。当然实际上这个状态空间不可是二维的，而是一个hypercube。以上就是最基本的权值计算方法，但是这种存储方式是及其浪费空间的。这个网络能够正确记忆的样本矢量数于神经元数目的比的极限大概是0.138。其中一个原因是因为当两个样本距离很近的时候，网络产生混淆，如下图所示：

       当蓝色的样本与绿色的样本叠加之后，无论输入的是类似于蓝色还是类似于绿色的任何一个输入，这个网络中的节点最终都会收敛于红色曲线的极小值点，这就是对两个样本发生了混淆，这里的红色极小值点被称为spurious minima。为了能够尽可能的提高Hopfield神经网络的存储能力，Hopfield, Feinstein 和 Palmer 在1985年提出了 unlearning 机制，这个方法被实验证明是有效的，但是缺乏理论分析。后来也有一些其它的方法来提高网络的存储能力，例如当新的样本到来时不时一次更新权值之后就结束，而是拿所有的样本来循环训练这个网络，大概就是增强记忆的感觉，证明也是有效的。

Reference：

1.https://en.wikipedia.org/wiki/Hopfield_network

2.https://en.wikipedia.org/wiki/Hopfield_network

3.https://www.zhihu.com/question/56994540/answer/191053894

4.http://mlexplore.org/2017/03/12/hopfield-networks-in-go/

5.http://www.asimovinstitute.org/neural-network-zoo/

6.https://www.zhihu.com/question/56994540/answer/191053894

7.http://web.cs.ucla.edu/~rosen/161/notes/hopfield.html

8.Hinton神经网络公开课11 Hopfield nets andBoltzmann machines