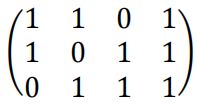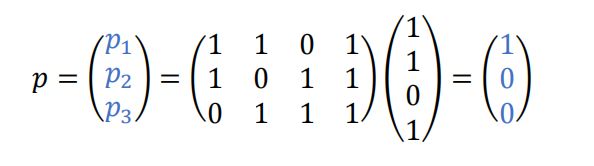海明码（Hamming Code）：基于矩阵思路的一些理解

在学习海明码之前，我们需要先理解什么是奇偶校验位（Parity bit）。

 

奇偶校验位

 

奇偶校验位是一种 错误检测码 ，它一般分为奇检验和偶校验。一般来说，在奇偶校验中，发送方会以一位作为奇偶校验位，而其余的位将作为信息位。奇偶校验的唯一作用就是 确保这条信息有奇数个1或者偶数个1 。

 

 

举个简单的例子，假设数据为 1010101010 ，此时数据中有5个1为奇数，所以对于奇校验来说，奇偶校验位为0；对于偶校验来说，奇偶校验位为1。

 

 

 

海明码

 

奇偶校验位的优点和缺点也很明显：优点即占用的位很少，缺点就是无法定位错误和检测偶数的错误。

 

 

而海明码的基本概念是 产生重叠的奇偶校验位 ，以便能够检测和纠正在数据位或 奇偶校验位中发生的错误。

 

 

[7-4] 海明码

 

                                                

以这张图为例，图中P为奇偶检验位（Parity bit），D为数据位（data）。

 

 

此时奇偶校验为偶校验。

 

 

我们可以很清晰的看到P1对D1，D2，D4做偶校验，P2对D1，D3，D4做偶校验，P3对D2，D3，D4做偶校验。

 

 

假设，发送方在完成偶校验之后将信息发送给接收方，但是由于信道的噪声干扰，其中一位数据位发生了翻转，接收方就可以通过检查奇偶校验来检查数据是否发生了翻转，并且通过多个奇偶校验位来进行定位。

 

 

如：接受方发现P1，D1，D2，D4中的1不为偶数（ D1，D2，D4中有错），P2，D1，D3，D4中的1也不为偶数（ D1，D3，D4中有错），但是P3，D2，D3，D4中的1为偶数（ D2，D3，D4中没错）， 我们就可以通过这些信息来得到发生翻转的位置为 D1。

 

 

 

通过上面的图，我们可以把信息归纳成一个表格：

 

 

在[7,4]海明码中，奇偶校验位放在1，2，4位，即2^n位。

当我们把2^n用二进制展开，就能理解放在此处的用意了：

1=001

2=010

4=100

8=1000

16=10000

etc.

即：

P1对 xxxx1 的数进行奇偶校验。

P2对 xxx1x 的数进行奇偶校验。

P3对 xx1xx 的数进行奇偶校验。

.......

海明码矩阵

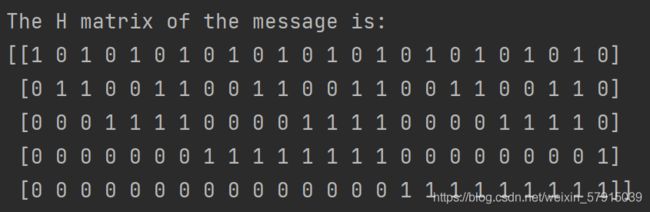
前面我们通过图得到表，当我们把表的数据拿下来做成一个矩阵，我们就能得到奇偶校验矩阵H：

然后我们能发现H的每一列都是位置的二进制表示，即

利用这一点，我们只要得到海明码的总长度，就能得到H：

用python举例：

输入任意长度的信息

计算之后得到编码的总长度

就可以得到 H(1-总长) 的奇偶校验矩阵H。

 

 

如果此时把H矩阵里代表奇偶校验位的列即2^n列删除

我们就能得到一个新的矩阵h

此时矩阵的每一行代表着一位奇偶校验位，因为P1对D1，D2，D4做偶校验，P2对D1，D3，D4做偶校验，P3对D2，D3，D4做偶校验。

所以此时h矩阵如果与代表原信息的矩阵相乘并余2的话，就相当让每个奇偶校验位对自己“管辖范围”里的数进行一次奇偶校验。

如：

P1=1*1+1*1+0*0+1*1=3, 余2位1（3个1）

P2=1*1+0*1+1*0+1*1=2, 余2位0（2个1）

P3=0*1+1*1+1*0+1*1=2, 余2位0（2个1）

 

此时把P放入2^n处

即可得到经过海明码编码后的数据：

也可以生成一个大矩阵G

先将奇偶校验位和信息位排列好，与信息相乘并余2后可直接得出结果

 

值得注意的是，这些矩阵都是动态的，可以随着输入的数据不同而进行拓展。