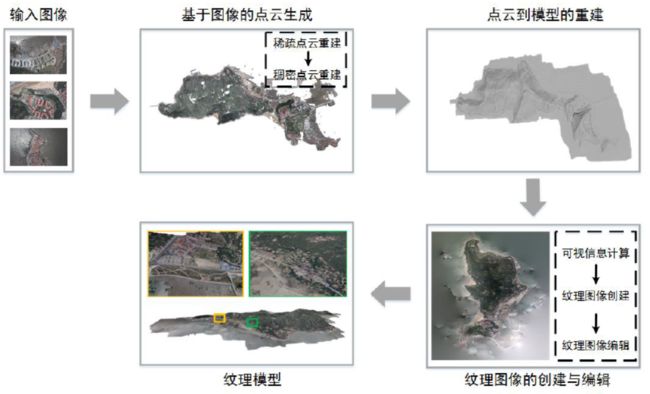
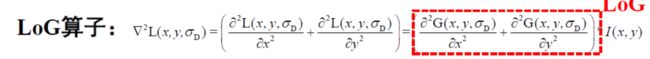徐凯_xp
徐凯_xp

1.特征点检测与匹配

三维模型重建的流程：
三维点云获取——几何结构恢复——场景绘制
三维点云获取：
1.激光雷达
2.微软Kinect
有效距离比较短
3.单目多视角 ：几乎很难实时
4.双目立体视觉

基于图像的三维模型重建：
1.输入图像
2.基于图像的点云生成
3.点云到模型的重建
4.纹理图像的创建与编辑
5.纹理模型


1.特征点检测与匹配_第1张图片

相关商业软件：
Acute3D,Altizure,Agisoft PhotoScan

图像特征点应用：
1.相机标定
2.图像拼接
3.稠密重建
4.场景理解

图像特征点的检测方法：

  1. 人工设计检测算法
  2. 基于深度学习的方法
  3. 场景中的人工标记点

图像特征点的基本要求：
1.差异性——可检测
特征点应该呈现出区别于非特征点的明显特征
2.重复性——可匹配
对应同一三维点的特征点应该在不同视角中被重复检测到

特征检测子（Feature Detector）

  1. Harris 角点检测
  2. 基于LoG的多尺度特征检测子//拉普拉斯的高斯
  3. 基于DoG的多尺度特征检测子//高斯差分的一种方法
  4. 快速特征点检测方法
特征点具有局部差异性

动机：特征点具有局部差异性
E(u,v) = \sum_{(x,y)}w(x,y){[I(x+u,y+v)-I(x,y)] }^2 \\ \approx \sum_{(x,y)}w(x,y){[I(x,y)+\frac{\partial{I}}{\partial{x}}(x,y)u+\frac{\partial{I}}{\partial{y}}(x,y)v-I(x,y)] }^2 \\= {\begin{bmatrix}u\\v \end{bmatrix}}^T {\begin{bmatrix}u\\v \end{bmatrix}}
图像梯度

Harris矩阵
H = {\begin{bmatrix}\sum_{(x,y)}W(x,y){\frac{\partial{I}}{\partial{x}}(x,y)}^2 &\sum_{(x,y)}W(x,y){\frac{\partial{I}}{\partial{x}}(x,y)}){\frac{\partial{I}}{\partial{y}}(x,y)} \\\sum_{(x,y)}W(x,y){\frac{\partial{I}}{\partial{x}}(x,y)}){\frac{\partial{I}}{\partial{y}}(x,y)} & \sum_{(x,y)}W(x,y){\frac{\partial{I}}{\partial{x}}(x,y)}^2 \end{bmatrix}}

1.特征点检测与匹配_第2张图片

以每个点为中心取一个窗口，窗口大小为5 5或者77，如果这个点具有差异性，往周围任意方向移动，周围的环境变化都是会比较大的，如果满足这个特性，我们就认为这个特征点具有明显的局部差异性。在工事中，I表示像素，如果是 彩色图像就是RGB,灰色图像就是灰度。(u,v)表示方向。然后对上式进行一阶泰勒展开。

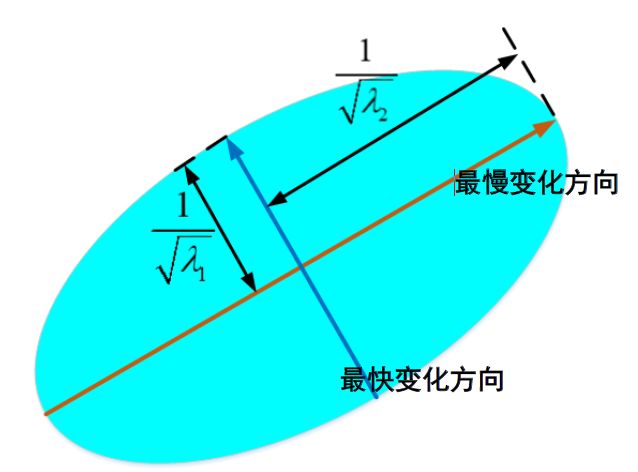
Harris矩阵H的特征值分析：

矩阵特征值反应了两个垂直方向的变化情况，一个事变化最快的方向，一个事变化最慢的方向

1.特征点检测与匹配_第3张图片

兴趣点位于光滑区域,不是特征点
，兴趣点位于边缘区域，
, 兴趣点位于角点区域
所以检测特征的任务转化为计算Harris矩阵，判断特征值大小。
在实际操作中，很少通过计算特征值来判断，因为计算特征值计算量比较大，取而代之的是Harris角点准则。

Harris角点准则


行列式值为特征值相乘，行列式的迹为特征值相加

  • K的值越小，检测子越敏感
  • 只有当和同时取得最大值时，C才能取得较大值
  • 避免了特征值分解，提高计策计算效率
非极大值抑制

在特征点附近，其他点的响应也比较大。
所以选取局部响应最大值，避免重复检测

Harris 角点检测

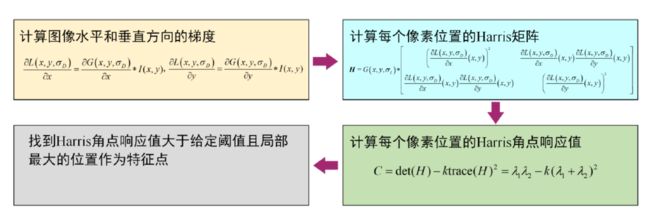
算法流程

  1. 计算图像水平和垂直方向的梯度
    但是在计算梯度之前，需要对图像进行滤波，一般进行高斯平阀，避免出现变化剧烈的值
  2. 计算每个像素位置的Harris矩阵
  3. 每个角点的响应值
  4. 非极大值抑制
1.特征点检测与匹配_第4张图片


Harris角点检测一般用于快速检测，比如视频里面的跟踪

基于LoG的特征检测子

动机：Harris角点检测不具有尺度不变性
LoG算子：Lindeberg(1993)提出Laplacian of Gaussian
(LoG)函数的极值点对应着特征点
Lindeberg(1993)提出Laplacian of Gaussian
(LoG)函数的极值点对应着特征点
尺度空间：
对于一幅图像，用不同大小的滤波核进行滤波，一般用高斯滤波，得到一系列图像，这些图像就称之为尺度空间。然后把这些图像摞起来

1.特征点检测与匹配_第5张图片


尺度归一化LoG算子：
1.特征点检测与匹配_第6张图片

  • 不同尺度下的LoG响应值不具有可比性
  • 构建尺度空间，同时在位置空间和尺度空间寻找归一化LoG极值（极大值/极小值）点作为特征点

LoG特征检测算法流程

1.特征点检测与匹配_第7张图片

LoG特征检测效果好，但是计算量比较大。
工程中也很少用。为了更好地利用LoG的性质，提出了一种近似的算法：基于DoG的特征检测子

LoG可以由DoG近似：
Lowe(2004)提出LoG近似等价于相邻尺度的高斯差分(DoG)
高斯空间：

高斯差分(DoG)

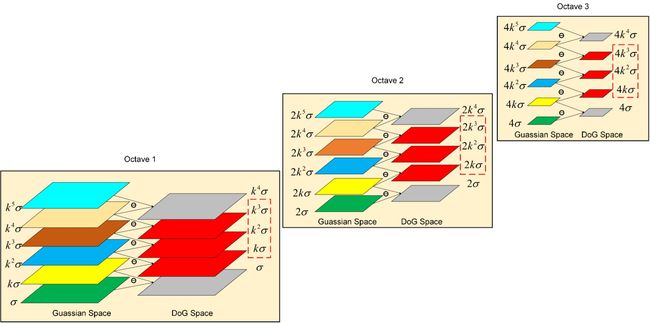
尺度空间构建
1.特征点检测与匹配_第8张图片

上图为3个Octive,每个octive的尺寸都会减小一半。
上图每个Octive中，左侧为高斯空间，相邻高斯空间做差得到DoG空间
特征点检测为在三维空间上做一个极值的比较，(三维空间为图像的二维空间+尺度的空间)，必须需要两个方向有极值。在高斯差分，边界上的两层是无效的，只有中间的红色区域是有效的。
在Octive,
if 每阶有效差分数 S =3，则高斯空间层数为N = S+3

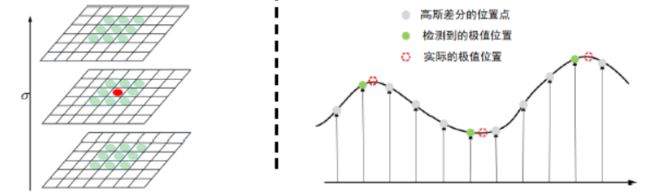
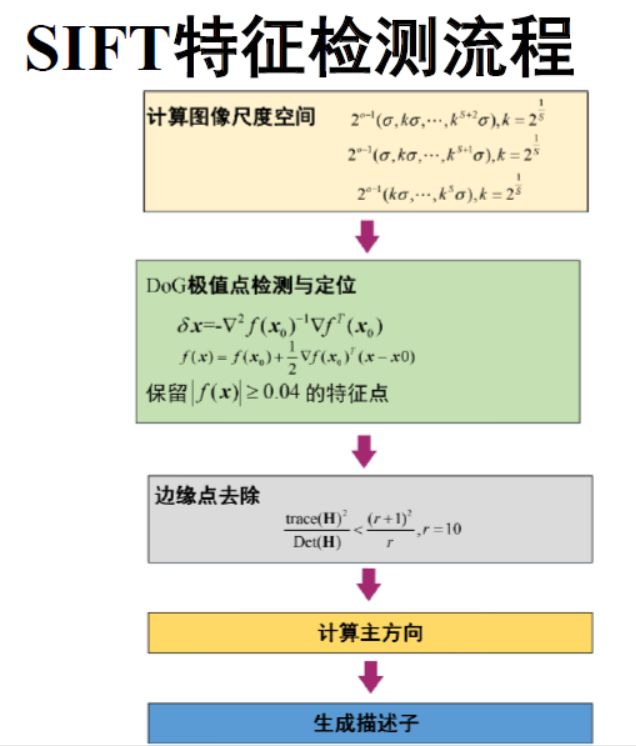
特征点位置确定:
在位置和尺度空间组成的三维空间中寻找极值点


1.特征点检测与匹配_第9张图片

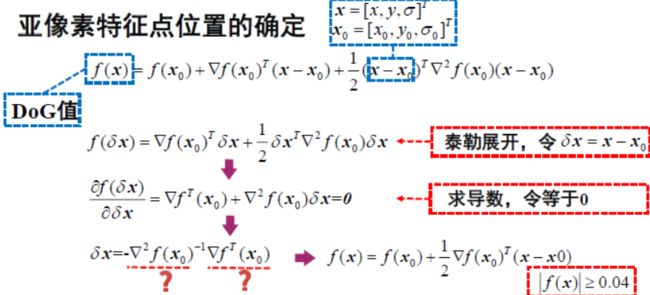
亚像素特征点位置确定：


1.特征点检测与匹配_第10张图片
1.特征点检测与匹配_第11张图片

1.特征点检测与匹配_第12张图片

除去边缘点：
DoG在边缘处值较大，需要避免检测到边缘点

计算主方向

通过统计梯度直方图的方法确定主方向，使算法具有旋转不变性


1.特征点检测与匹配_第13张图片

1.特征点检测与匹配_第14张图片

旋转 不变性、 尺度 不变性 、亮度 变化 不变性 ，对视角变化、 仿射 变换有一定程度的稳性
SIFT特征点非常稳定和鲁棒，但是计算量很大，对于要求稳定的图像建模可以采用。
针对实时要求比较高的应用提出了快速特征检测。

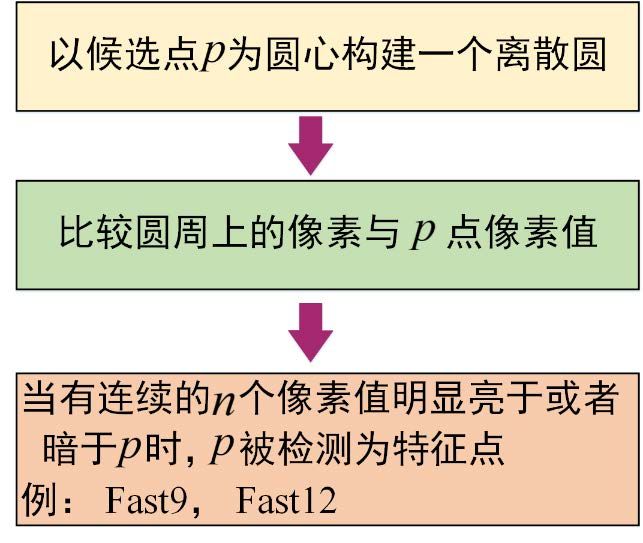
快速特征检测

FAST特征点(Feature from Accelerated Segment Test)
通过检测局部像素灰度变化来确认特征点的位置


1.特征点检测与匹配_第15张图片

1.特征点检测与匹配_第16张图片

速度快，SIFT的一百倍，不具有尺度和旋转不变性

Oriented FAST(ORB)
  • 为了获取尺度不变性
    构建图像金字塔，在金字塔每一层上上检测关键点。
  • 获取旋转不变性
    通过灰度质心法(Intensity Centroid)确定图像主方向
1.特征点检测与匹配_第17张图片

特征描述子(Feature Descriptor)

基于直方图的描述子
基于不变性的描述子
二进制描述子

  • 每个特征点独特的身份认证
  • 同一空间点在不同视角的特征点具有高度相似的描述子
  • 不同特征点的描述子差异性尽量大
  • 通常描述子是一个具有固定长度的向量(可以理解为一个特征)
特征支持区域：

以特征点为中心取一块区域，有圆形或者矩形，称之为特征支持区域
主方向：进行旋转并重新插值
特征尺度：影响支持区域的大小


1.特征点检测与匹配_第18张图片
基于直方图的描述子

用于微小运动的描述子
以特征点为中心的矩形区域内所有
像素的灰度值作为描述子,拉成一个向量，计算向量间距离

适用于微小变化的图像
对图像存在明显的旋转、尺度、光照和透视变换时不稳定

SIFT描述子--旋转主方向

根据主方向对支持区域进行旋转，并通过双线性插值重构
减去均值再除以方差
图像归一化处理，去除光照变化

1.特征点检测与匹配_第19张图片

过程：
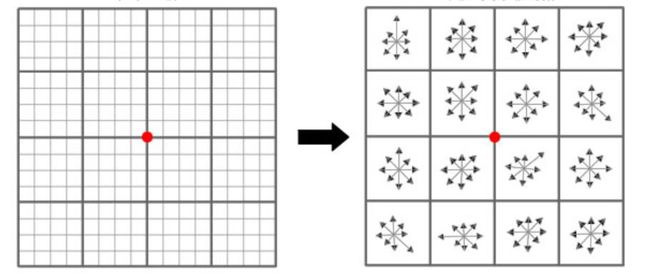
1.统计局部梯度信息
将区域划分成4 4的block
每个 block 内统计梯度方向 的直方图 (高斯加权梯度 作为系数 )
1.特征点检测与匹配_第20张图片
高斯加权保证距离特征点近的像素作用更大，梯度直方图计算8个方向

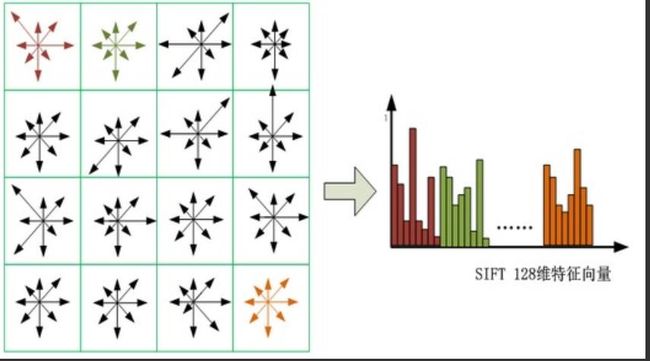
每个block，统计8个方向的直方图，将16个block拉成一列，那就是168 = 128
SIFT描述子——生成描述子
1.特征点检测与匹配_第21张图片

SIFT描述子——归一化处理

  • 门限处理—直方图每个方向的梯度幅值不超过0.2
  • 描述子长度归一化
    归一化处理提升了特征点光度变化的不变性
    SIFT描述子变种：PCA-SIFT/SURF
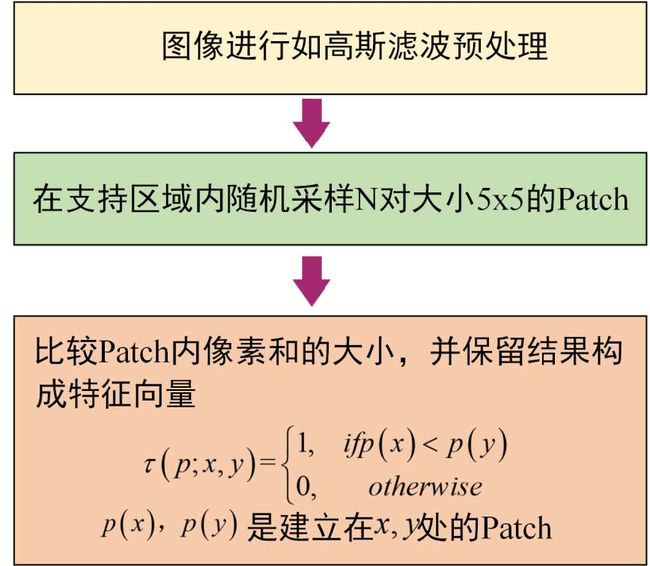
二进制描述子

描述子形式：
描述向量由N个0或者1组成
N= 128，256,512
生成速度快，匹配效率高，不具有旋转不变性

1.特征点检测与匹配_第22张图片

为了使其具有旋转不变性
N对采样点

根据特征点的主方向计算旋转

在新的采样点上进行BRIEF描述子生成
1.特征点检测与匹配_第23张图片

特征匹配

  • 距离度量
  • 匹配策略
  • 高效匹配
  • 特征匹配验证
    问题描述：
    计算两幅图中特征描述子的匹配关系
距离度量
1.特征点检测与匹配_第24张图片

匹配策略

最近邻搜索

最近邻距离比(lowe-ratio)

最近邻距离和次近邻距离比小于一定值

1.特征点检测与匹配_第25张图片

高效匹配

快速最近邻搜索
哈希表
多维Kd-tree

特征匹配

BFM(Bruce Force Mather)匹配ORB的结果


1.特征点检测与匹配_第26张图片
选择最好的 50 个匹配结果进行显示

错误的匹配可以通过估计相机模型方式去除
估计 Homography Homography 矩阵之前最好的 50 对匹配对

你可能感兴趣的:(1.特征点检测与匹配)

  • 斤斤计较的婚姻到底有多难？ 白心之岂必有为
    很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
  • QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
    功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • android系统selinux中添加新属性property 辉色投像
    1.定位/android/system/sepolicy/private/property_contexts声明属性开头：persist.charge声明属性类型：u:object_r:system_prop:s0图12.定位到android/system/sepolicy/public/domain.te删除neverallow{domain-init}default_prop:property
  • 随笔 | 仙一般的灵气 海思沧海
    仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
  • 一百九十四章. 自相矛盾 巨木擎天
    唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
  • C语言如何定义宏函数？ 小九格物 c语言
    在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
  • 微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务java架构
    在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 学点心理知识，呵护孩子健康 静候花开_7090
    昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
  • 2021年12月19日，春蕾教育集团团建活动感受——黄晓丹 黄错错加油
    感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
  • c++ 的iostream 和 c++的stdio的区别和联系 黄卷青灯77 c++算法开发语言iostreamstdio
    在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
  • 《投行人生》读书笔记 小蘑菇的树洞
    《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
  • Long类型前后端数据不一致 igotyback 前端
    响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
  • Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类qt开发语言sdl2linux
    需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
  • 店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码 说私域 人工智能小程序
    摘要：本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合，阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇，提升了用户信任感、拓展了营销渠道，并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展，社区团购作为一种新兴的商业模式，在满足消费者日常需
  • 向内而求 陈陈_19b4
    10月27日，阴。阅读书目:《次第花开》。作者:希阿荣博堪布，是当今藏传佛家宁玛派最伟大的上师法王，如意宝晋美彭措仁波切颇具影响力的弟子之一。多年以来，赴海内外各地弘扬佛法，以正式授课、现场开示、发表文章等多种方法指导佛学弟子修行佛法。代表作《寂静之道》、《生命这出戏》、《透过佛法看世界》自出版以来一直是佛教类书籍中的畅销书。图片发自App金句:1.佛陀说，一切痛苦的根源在于我们长期以来对自身及外
  • 2021-08-26 影幽
    在生活中，女人与男人的感悟往往有所不同。人生最大的舞台就是生活，大幕随时都可能拉开，关键是你愿不愿意表演都无法躲避。在生活中，遇事不要急躁，不要急于下结论，尤其生气时不要做决断，要学会换位思考，大事化小小事化了，把复杂的事情尽量简单处理，千万不要把简单的事情复杂化。永远不要扭曲，别人善意，无药可救。昨天是张过期的支票，明天是张信用卡，只有今天才是现金，要善加利用！执着的攀登者不必去与别人比较自己的
  • 高级编程--XML+socket练习题 masa010 java开发语言
    1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人（1）使用dom4j将信息存入xml中（2）读取信息，并打印控制台（3）添加一个city节点与子节点（4）使用socketTCP协议编写服务端与客户端，客户端输入城市ID，服务器响应相应城市信息（5）使用socketTCP协议编写服务端与客户端，客户端要求用户输入city对象，服务端接收并使用dom4j
  • 2018-07-23-催眠日作业-#不一样的31天#-66小鹿 小鹿_33
    预言日：人总是在逃避命运的路上，与之不期而遇。心理学上有个著名的名词，叫做自证预言；经济学上也有一个很著名的定律叫做，墨菲定律；在灵修派上，还有一个很著名的法则，叫做吸引力法则。这3个领域的词，虽然看起来不太一样，但是他们都在告诉人们一个现象：你越担心什么，就越有可能会发生什么。同样的道理，你越想得到什么，就应该要积极地去创造什么。无论是自证预言，墨菲定律还是吸引力法则，对人都有正反2个维度的影响
  • 水平垂直居中的几种方法（总结） LJ小番茄 CSS_玄学语言htmljavascript前端csscss3
    1.使用flexbox的justify-content和align-items.parent{display:flex;justify-content:center;/*水平居中*/align-items:center;/*垂直居中*/height:100vh;/*需要指定高度*/}2.使用grid的place-items:center.parent{display:grid;place-item
  • 回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录leetcode算法职场和发展
    重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
  • 每日一题——第九十题 互联网打工人no1 C语言程序设计每日一练c语言
    题目：判断子串是否与主串匹配#include#include#include//////判断子串是否在主串中匹配//////主串///子串///boolisSubstring(constchar*str,constchar*substr){intlenstr=strlen(str);//计算主串的长度intlenSub=strlen(substr);//计算子串的长度//遍历主字符串，对每个可能得
  • Python数据分析与可视化实战指南 William数据分析 pythonpython数据
    在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
  • 《庄子.达生9》 钱江潮369
    【原文】孔子观于吕梁，县水三十仞，流沫四十里，鼋鼍鱼鳖之所不能游也。见一丈夫游之，以为有苦而欲死也，使弟子并流而拯之。数百步而出，被发行歌而游于塘下。孔子从而问焉，曰：“吾以子为鬼，察子则人也。请问，‘蹈水有道乎’”曰：“亡，吾无道。吾始乎故，长乎性，成乎命。与齐俱入，与汩偕出，从水之道而不为私焉。此吾所以蹈之也。”孔子曰：“何谓始乎故，长乎性，成乎命？”曰：“吾生于陵而安于陵，故也；长于水而安于
  • Python中os.environ基本介绍及使用方法 鹤冲天Pro #Pythonpython服务器开发语言
    文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
  • 水泥质量纠纷案代理词 徐宝峰律师
    贵州领航建设有限公司诉贵州纳雍隆庆乌江水泥有限公司产品质量纠纷案代理词尊敬的审判长、审判员：贵州千里律师事务所接受被告贵州纳雍隆庆乌江水泥有限公司的委托，指派我担任其诉讼代理人，参加本案的诉讼活动。下面，我结合本案事实和相关法律规定发表如下代理意见，供合议庭评议案件时参考：原告应当举证证明其遭受的损失与被告生产的水泥质量的因果关系。首先水泥是一种粉状水硬性无机胶凝材料。加水搅拌后成浆体，能在空气中
  • 怎么起诉借钱不还的人？怎样起诉欠款不还的人？ 影子爱学习
    怎么起诉借钱不还的人？怎样起诉欠款不还的人？如果遇到难以解决的法律问题，我们可以匹配专业律师。例如：婚姻家庭（离婚纠纷）、刑事辩护、合同纠纷、债权债务、房产（继承）纠纷、交通事故、劳动争议、人身损害、公司相关法律事务（法律顾问）等咨询推荐手机/微信:15633770876【全国案件皆可】借钱不还起诉对方需要哪些资料起诉欠钱不还的，一般需要的材料包括以下这些：借据、收据、欠条、付款凭证等证据，以及向
  • linux sdl windows.h,Windows下的SDL安装 奔跑吧linux内核 linuxsdlwindows.h
    首先你要下载并安装SDL开发包。如果装在C盘下，路径为C:\SDL1.2.5如果在WINDOWS下。你可以按以下步骤：1.打开VC++，点击"Tools",Options2,点击directories选项3.选择"Includefiles"增加一个新的路径。"C:\SDL1.2.5\include"4，现在选择"Libaryfiles“增加"C:\SDL1.2.5\lib"现在你可以开始编写你的第
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • mongodb3.03开启认证 21jhf mongodb
    下载了最新mongodb3.03版本，当使用--auth 参数命令行开启mongodb用户认证时遇到很多问题，现总结如下： （百度上搜到的基本都是老版本的，看到db.addUser的就是，请忽略） Windows下我做了一个bat文件，用来启动mongodb，命令行如下： mongod --dbpath db\data --port 27017 --directoryperdb --logp
  • 【Spark103】Task not serializable bit1129 Serializable
    Task not serializable是Spark开发过程最令人头疼的问题之一，这里记录下出现这个问题的两个实例，一个是自己遇到的，另一个是stackoverflow上看到。等有时间了再仔细探究出现Task not serialiazable的各种原因以及出现问题后如何快速定位问题的所在，至少目前阶段碰到此类问题，没有什么章法 1.   package spark.exampl
  • 你所熟知的 LRU(最近最少使用) dalan_123 java
    关于LRU这个名词在很多地方或听说，或使用，接下来看下lru缓存回收的实现 1、大体的想法     a、查询出最近最晚使用的项     b、给最近的使用的项做标记 通过使用链表就可以完成这两个操作，关于最近最少使用的项只需要返回链表的尾部；标记最近使用的项，只需要将该项移除并放置到头部，那么难点就出现 你如何能够快速在链表定位对应的该项？ 这时候多
  • Javascript 跨域 周凡杨 JavaScriptjsonp跨域cross-domain
                                       
  • linux下安装apache服务器 g21121 apache
    安装apache 下载windows版本apache，下载地址：http://httpd.apache.org/download.cgi   1.windows下安装apache Windows下安装apache比较简单，注意选择路径和端口即可，这里就不再赘述了。 2.linux下安装apache： 下载之后上传到linux的相关目录，这里指定为/home/apach
  • FineReport的JS编辑框和URL地址栏语法简介 老A不折腾 finereportweb报表报表软件语法总结
      JS编辑框： 1.FineReport的js。 作为一款BS产品，browser端的JavaScript是必不可少的。 FineReport中的js是已经调用了finereport.js的。 大家知道，预览报表时，报表servlet会将cpt模板转为html，在这个html的head头部中会引入FineReport的js，这个finereport.js中包含了许多内置的fun
  • 根据STATUS信息对MySQL进行优化 墙头上一根草 status
    mysql  查看当前正在执行的操作，即正在执行的sql语句的方法为:      show processlist 命令   mysql> show global status;可以列出MySQL服务器运行各种状态值，我个人较喜欢的用法是show status like '查询值%';一、慢查询mysql> show variab
  • 我的spring学习笔记7-Spring的Bean配置文件给Bean定义别名 aijuans Spring 3
    本文介绍如何给Spring的Bean配置文件的Bean定义别名？ 原始的 <bean id="business" class="onlyfun.caterpillar.device.Business"> <property name="writer"> <ref b
  • 高性能mysql 之 性能剖析 annan211 性能mysqlmysql 性能剖析剖析
    1 定义性能优化 mysql服务器性能，此处定义为 响应时间。 在解释性能优化之前，先来消除一个误解，很多人认为，性能优化就是降低cpu的利用率或者减少对资源的使用。 这是一个陷阱。 资源时用来消耗并用来工作的，所以有时候消耗更多的资源能够加快查询速度，保持cpu忙绿，这是必要的。很多时候发现 编译进了新版本的InnoDB之后，cpu利用率上升的很厉害，这并不
  • 主外键和索引唯一性约束 百合不是茶 索引唯一性约束主外键约束联机删除
    目标;第一步;创建两张表 用户表和文章表         第二步;发表文章       1,建表; ---用户表 BlogUsers --userID唯一的 --userName --pwd --sex create
  • 线程的调度 bijian1013 java多线程thread线程的调度java多线程
    1.       Java提供一个线程调度程序来监控程序中启动后进入可运行状态的所有线程。线程调度程序按照线程的优先级决定应调度哪些线程来执行。   2.       多数线程的调度是抢占式的（即我想中断程序运行就中断，不需要和将被中断的程序协商） a) 
  • 查看日志常用命令 bijian1013 linux命令unix
    一.日志查找方法，可以用通配符查某台主机上的所有服务器grep "关键字" /wls/applogs/custom-*/error.log   二.查看日志常用命令1.grep '关键字' error.log：在error.log中搜索'关键字'2.grep -C10 '关键字' error.log：显示关键字前后10行记录3.grep '关键字' error.l
  • 【持久化框架MyBatis3一】MyBatis版HelloWorld bit1129 helloworld
    MyBatis这个系列的文章，主要参考《Java Persistence with MyBatis 3》。   样例数据 本文以MySQL数据库为例，建立一个STUDENTS表，插入两条数据，然后进行单表的增删改查     CREATE TABLE STUDENTS ( stud_id int(11) NOT NULL AUTO_INCREMENT,
  • 【Hadoop十五】Hadoop Counter bit1129 hadoop
       1. 只有Map任务的Map Reduce Job File System Counters FILE: Number of bytes read=3629530 FILE: Number of bytes written=98312 FILE: Number of read operations=0 FILE: Number of lar
  • 解决Tomcat数据连接池无法释放 ronin47 tomcat 连接池　优化
    近段时间，公司的检测中心报表系统(SMC)的开发人员时不时找到我，说用户老是出现无法登录的情况。前些日子因为手头上 有Jboss集群的测试工作，发现用户不能登录时，都是在Tomcat中将这个项目Reload一下就好了，不过只是治标而已，因为大概几个小时之后又会 再次出现无法登录的情况。 今天上午，开发人员小毛又找到我，要我协助将这个问题根治一下，拖太久用户难保不投诉。 简单分析了一
  • java-75-二叉树两结点的最低共同父结点 bylijinnan java
    import java.util.LinkedList; import java.util.List; import ljn.help.*; public class BTreeLowestParentOfTwoNodes { public static void main(String[] args) { /* * node data is stored in
  • 行业垂直搜索引擎网页抓取项目 carlwu LuceneNutchHeritrixSolr
    公司有一个搜索引擎项目，希望各路高人有空来帮忙指导，谢谢！ 这是详细需求： （1） 通过提供的网站地址(大概100-200个网站)，网页抓取程序能不断抓取网页和其它类型的文件（如Excel、PDF、Word、ppt及zip类型），并且程序能够根据事先提供的规则，过滤掉不相干的下载内容。 （2） 程序能够搜索这些抓取的内容，并能对这些抓取文件按照油田名进行分类，然后放到服务器不同的目录中。
  • [通讯与服务]在总带宽资源没有大幅增加之前,不适宜大幅度降低资费 comsci 资源
          降低通讯服务资费，就意味着有更多的用户进入，就意味着通讯服务提供商要接待和服务更多的用户，在总体运维成本没有由于技术升级而大幅下降的情况下，这种降低资费的行为将导致每个用户的平均带宽不断下降，而享受到的服务质量也在下降，这对用户和服务商都是不利的。。。。。。。。     &nbs
  • Java时区转换及时间格式 Cwind java
    本文介绍Java API 中 Date, Calendar, TimeZone和DateFormat的使用，以及不同时区时间相互转化的方法和原理。   问题描述： 向处于不同时区的服务器发请求时需要考虑时区转换的问题。譬如，服务器位于东八区（北京时间，GMT+8:00），而身处东四区的用户想要查询当天的销售记录。则需把东四区的“今天”这个时间范围转换为服务器所在时区的时间范围。
  • readonly,只读，不可用 dashuaifu jsjspdisablereadOnlyreadOnly
    readOnly 和 readonly 不同，在做js开发时一定要注意函数大小写和jsp黄线的警告！！！我就经历过这么一件事： 使用readOnly在某些浏览器或同一浏览器不同版本有的可以实现“只读”功能，有的就不行，而且函数readOnly有黄线警告！！！就这样被折磨了不短时间！！！（期间使用过disable函数，但是发现disable函数之后后台接收不到前台的的数据！！！）  
  • LABjs、RequireJS、SeaJS 介绍 dcj3sjt126com jsWeb
    LABjs 的核心是 LAB（Loading and Blocking）：Loading 指异步并行加载，Blocking 是指同步等待执行。LABjs 通过优雅的语法（script 和 wait）实现了这两大特性，核心价值是性能优化。LABjs 是一个文件加载器。RequireJS 和 SeaJS 则是模块加载器，倡导的是一种模块化开发理念，核心价值是让 JavaScript 的模块化开发变得更
  • [应用结构]入口脚本 dcj3sjt126com PHPyii2
    入口脚本 入口脚本是应用启动流程中的第一环，一个应用（不管是网页应用还是控制台应用）只有一个入口脚本。终端用户的请求通过入口脚本实例化应用并将将请求转发到应用。 Web 应用的入口脚本必须放在终端用户能够访问的目录下，通常命名为 index.php，也可以使用 Web 服务器能定位到的其他名称。 控制台应用的入口脚本一般在应用根目录下命名为 yii（后缀为.php），该文
  • haoop shell命令 eksliang hadoophadoop shell
    cat chgrp chmod chown copyFromLocal copyToLocal cp du dus expunge get getmerge ls lsr mkdir movefromLocal mv put rm rmr setrep stat tail test text
  • MultiStateView不同的状态下显示不同的界面 gundumw100 android
    只要将指定的view放在该控件里面，可以该view在不同的状态下显示不同的界面，这对ListView很有用，比如加载界面，空白界面，错误界面。而且这些见面由你指定布局，非常灵活。 PS：ListView虽然可以设置一个EmptyView，但使用起来不方便，不灵活，有点累赘。 <com.kennyc.view.MultiStateView xmlns:android=&qu
  • jQuery实现页面内锚点平滑跳转 ini JavaScripthtmljqueryhtml5css
    平时我们做导航滚动到内容都是通过锚点来做，刷的一下就直接跳到内容了，没有一丝的滚动效果，而且 url 链接最后会有“小尾巴”，就像#keleyi，今天我就介绍一款 jquery 做的滚动的特效，既可以设置滚动速度，又可以在 url 链接上没有“小尾巴”。   效果体验：http://keleyi.com/keleyi/phtml/jqtexiao/37.htmHTML文件代码： &
  • kafka offset迁移 kane_xie kafka
    在早前的kafka版本中（0.8.0），offset是被存储在zookeeper中的。   到当前版本（0.8.2）为止，kafka同时支持offset存储在zookeeper和offset manager（broker）中。   从官方的说明来看，未来offset的zookeeper存储将会被弃用。因此现有的基于kafka的项目如果今后计划保持更新的话，可以考虑在合适
  • android > 搭建 cordova 环境 mft8899 android
      1 , 安装 node.js        http://nodejs.org      node -v   查看版本   2, 安装 npm   可以先从  https://github.com/isaacs/npm/tags  下载 源码 解压到
  • java封装的比较器，比较是否全相同，获取不同字段名字 qifeifei
     非常实用的java比较器，贴上代码： import java.util.HashSet; import java.util.List; import java.util.Set; import net.sf.json.JSONArray; import net.sf.json.JSONObject; import net.sf.json.JsonConfig; i
  • 记录一些函数用法 .Aky. 位运算PHP数据库函数IP
    高手们照旧忽略。 想弄个全天朝IP段数据库，找了个今天最新更新的国内所有运营商IP段，copy到文件，用文件函数，字符串函数把玩下。分割出startIp和endIp这样格式写入.txt文件，直接用phpmyadmin导入.csv文件的形式导入。（生命在于折腾，也许你们觉得我傻X，直接下载人家弄好的导入不就可以，做自己的菜鸟，让别人去说吧） 当然用到了ip2long()函数把字符串转为整型数
  • sublime text 3 rust wudixiaotie Sublime Text
    1.sublime text 3 => install package => Rust 2.cd ~/.config/sublime-text-3/Packages 3.mkdir rust 4.git clone https://github.com/sp0/rust-style 5.cd rust-style 6.cargo build --release 7.ctrl
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他