Python小白 Leetcode刷题历程 No.61-No.65 旋转链表、不同路径、不同路径Ⅱ、最小路径和、有效数字
写在前面:
作为一个计算机院的大学生,总觉得仅仅在学校粗略的学习计算机专业课是不够的,尤其是假期大量的空档期,作为一个小白,实习也莫得路子,又不想白白耗费时间。于是选择了Leetcode这个平台来刷题库。编程我只学过基础的C语言,现在在自学Python,所以用Python3.8刷题库。现在我Python掌握的还不是很熟练,算法什么的也还没学,就先不考虑算法上的优化了,单纯以解题为目的,复杂程度什么的以后有时间再优化。计划顺序五个题写一篇日志,希望其他初学编程的人起到一些帮助,写算是对自己学习历程的一个见证了吧。
有一起刷LeetCode的可以关注我一下,我会一直发LeetCode题库Python3解法的,也可以一起探讨。
觉得有用的话可以点赞关注下哦,谢谢大家!
········································································································································································
题解框架:
1.题目,难度
2.题干,题目描述
3.题解代码(Python3(不是Python,是Python3))
4.或许有用的知识点(不一定有)
5.解题思路
6.优解代码及分析(当我发现有比我写的好很多的代码和思路我就会写在这里)
········································································································································································
No.61.旋转链表
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def rotateRight(self, head: ListNode, k: int) -> ListNode:
if (not head) or (not head.next) :
return None if not head else head
old_tail = head
n = 1
while old_tail.next:
old_tail = old_tail.next
n += 1
old_tail.next = head
new_tail = head
for i in range(n - k%n -1):
new_tail =new_tail.next
new_head =new_tail.next
new_tail.next = None
return new_head
或许有用的知识点:
这道题可以使用快慢指针的思想。
解题思路:
链表中的点已经相连,一次旋转操作意味着:先将链表闭合成环,再找到相应的位置断开这个环,确定新的链表头和链表尾。所以,我们首先找到旧的尾部并将其与链表头相连old_tail.next = head,整个链表闭合成环,同时计算出链表的长度n;找到新的尾部,第 (n-k%n-1)个节点,新的链表头是第(n-k%n)个节点;断开环 new_tail.next = None,并返回新的链表头 new_head即可。
优解代码及分析:
优解代码(Python3.8)
class Solution:
def rotateRight(self, head: ListNode, k: int) -> ListNode:
# 下面有 if n==0 ...判断了,所以开头的判断可以省略
#if not head or k<=0:
# return head
# 创建一个哑节点,快指针,慢指针,统计节点个数的cur
dummy = ListNode(-1)
cur,n,fast,low,dummy.next = head,0,dummy,dummy,head
# 统计链表个数
while cur:
cur,n = cur.next,n+1
# 边界条件不要忘记处理了
if n==0 or k%n==0:
return head
# 还有一个边界条件不要忘了,k可能大于n,所以要取模
n = k%n
# 快指针先移动n步
while fast.next and n>0:
fast,n = fast.next,n-1
# 快指针,慢指针一起移动,找到需要切割的点
while fast.next:
low,fast = low.next,fast.next
# 改变链表的指向关系,注意这里的步骤不要乱了
# 先让fast节点指向head(也就是dummy.next)
# 再是head(也就是dummy.next)指向low的下一个节点
# 这两步如果弄反了就会出现节点丢失了
# 最后不要忘记将low.next置空
fast.next,dummy.next,low.next = head,low.next,None
return dummy.next
分析;
双指针法写起来思路比较清楚,代码比较简单,代码中有着极详细的注释,应该比较容易理解。
No.62.不同路径
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
#第一行/第一列每个格都只有一种走法
dp = [[1]*n] + [[1]+[0]*(n-1) for _ in range(m-1)]
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[m-1][n-1]
或许有用的知识点:
这道题要用到动态规划的方法。
解题思路:
这道题可以使用动态规划的方法,套用动态规划的模板,对于这道题,假设dp[i][j]是从左上角到第i行第j列的方格有多少总走法,动态规划的三要素分别为:
状态:第一行和第一列都只有一种走法,其他格子走法=上面一格的走法+左边一格的走法
状态转移方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]
边界条件: dp = [[1]n] + [[1]+[0](n-1) for _ in range(m-1)]
空间复杂度:O(n²)
优解代码及分析:
优解代码(Python3.8)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
cur = [1]*n
for i in range(1,m):
for j in range(1,n):
cur[j] += cur[j-1]
return cur[n-1]
分析:
其实也是动态规划的思想,只不过将创建的空间减少了一个维度,空间复杂度O(n)。
No.63.不同路径Ⅱ
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
if (not obstacleGrid) or (not obstacleGrid[0]):
return 0
l_row = len(obstacleGrid)
l_col = len(obstacleGrid[0])
dp = [ [0]*l_col for _ in range(l_row)]
#首位置
dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0
if dp[0][0] == 0:
return 0
#第一行
for j in range(1,l_col):
if obstacleGrid[0][j] != 1:
dp[0][j] = dp[0][j-1]
#第一列
for i in range(1,l_row):
if obstacleGrid[i][0] != 1:
dp[i][0] = dp[i-1][0]
#剩余位置
for i in range(1,l_row):
for j in range(1,l_col):
if obstacleGrid[i][j] != 1:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[l_row-1][l_col-1]
或许有用的知识点:
这道题要用到动态规划的方法。
解题思路:
这道题根上一道题‘No.62.不同路径’很相似,是上一题的加强版。
这道题可以使用动态规划的方法,套用动态规划的模板,对于这道题,假设dp[i][j]是从左上角到第i行第j列的方格有多少总走法,动态规划的三要素分别为:
状态:第一行和第一列都只有一种走法,其他格子走法=上面一格的走法+左边一格的走法;但如果这一格有障碍物,该格的dp=0。
状态转移方程:if obstacleGrid[i][j] != 1: dp[i][j] = dp[i-1][j] + dp[i][j-1]
边界条件:
(#首位置)dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0 ;
(#第一行)if obstacleGrid[0][j] != 1: dp[0][j] = dp[0][j-1];
(#第一列)if obstacleGrid[i][j] != 1: dp[i][j] = dp[i-1][j] + dp[i][j-1]。
No.64.最小路径和
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
if (not grid) or (not grid[0]):
return 0
m = len(grid)
n = len(grid[0])
dp = [[0]*n for _ in range(m)]
dp[0][0] = grid[0][0] #首位
for j in range(1,n): #第一行
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1,m): #第一列
dp[i][0] = dp[i-1][0] + grid[i][0]
for i in range(1,m):
for j in range(1,n):
dp[i][j] = min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])
return dp[m-1][n-1]
或许有用的知识点:
这道题要用到动态规划的方法。
解题思路:
这道题可以使用动态规划的方法,套用动态规划的模板,对于这道题,假设dp[i][j]是从左上角到第i行第j列的方格路径的数字总和最小值,动态规划的三要素分别为:
状态:第一行和第一列都只有一种走法,其他格子的路径的数字总和最小值=(上面一格的路径的数字总和最小值+第i行第j列的方格的数字) 和 (左边一格的路径的数字总和最小值+第i行第j列的方格的数字)二者之间的最小值。
状态转移方程:dp[i][j] = min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])
边界条件:
(#首位置) dp[0][0] = grid[0][0] ;
(#第一行)for j in range(1,n): dp[0][j] = dp[0][j-1] + grid[0][j];
(#第一列)for i in range(1,m): dp[i][0] = dp[i-1][0] + grid[i][0]。
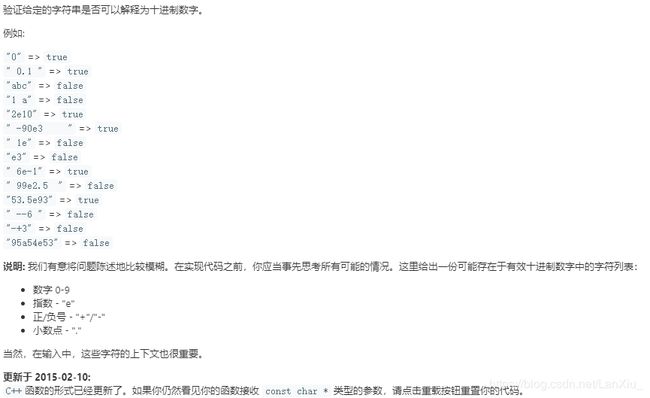
No.65.有效数字
难度:困难
题目描述:
题解代码(Python3.8)
class Solution:
def isNumber(self, s: str) -> bool:
state = [
{},
# 状态1,初始状态(扫描通过的空格)
{"blank": 1, "sign": 2, "digit": 3, ".": 4},
# 状态2,发现符号位(后面跟数字或者小数点)
{"digit": 3, ".": 4},
# 状态3,数字(一直循环到非数字)
{"digit": 3, ".": 5, "e": 6, "blank": 9},
# 状态4,小数点(后面只有紧接数字)
{"digit": 5},
# 状态5,小数点之后(后面只能为数字,e,或者以空格结束)
{"digit": 5, "e": 6, "blank": 9},
# 状态6,发现e(后面只能符号位, 和数字)
{"sign": 7, "digit": 8},
# 状态7,e之后(只能为数字)
{"digit": 8},
# 状态8,e之后的数字后面(只能为数字或者以空格结束)
{"digit": 8, "blank": 9},
# 状态9, 终止状态 (如果发现非空,就失败)
{"blank": 9}
]
cur_state = 1
for c in s:
if c.isdigit():
c = "digit"
elif c in " ":
c = "blank"
elif c in "+-":
c = "sign"
if c not in state[cur_state]:
return False
cur_state = state[cur_state][c]
if cur_state not in [3, 5, 8, 9]:
return False
return True
或许有用的知识点:
这道题要用到有限状态机(FSM),或者说有限状态机的一种特殊状态——有限自动机(DFA)的思想(在数字电路基础、Verilog、离散数学等大学专业课中应该学习过)。
解题思路:
以下为一个考虑到各种情况的有限自动机模型,状态机的结构可以结合代码中的注释一起理解。(自己设计一个状态机有时不能一开始就考虑到所有情况,要多测试不同情况)。我们的代码先创建一个state包含状态机的所有状态与内容,之和将字符串中的字符依次放入状态机运行,最后查看状态机的状态是否在指定状态即可。