0. 写在前面
在3dmm中,重要的一步是对3d模型进行拍照。
这里引出问题:怎么给3d模型拍照?
下面先解决这个拍照问题。
1. 相机模型
本节目标:
- 理解针孔相机的模型,内参与径向畸变参数。
- 理解一个空间点是如何投影到相机成像。
我们知道:
一张照片(二维):由多个像素组成,每个像素记录了色彩或亮度的信息。
一个物体(三维世界):物体反射或发出的光线,通过相机光心后,投影到相机的成像平面。
相机将三维世界中的坐标点(单位米)映射到二维图像平面(单位像素)的过程能够用一个几何模型进行描述。
这个模型有很多种,其中最简单的为针孔模型。事实上,真实的相机镜头是透镜,会使得光线投影到成像平面的过程会产生畸变。
那么总结一下,所谓相机模型实际是是:针孔相机模型+畸变模型。
在3dmm中我们暂不考虑畸变模型。
1.1 针孔相机模型 (Pinhole camera)
在小孔成像过程中,小孔模型将三维世界中的蜡烛投影到一个二维成像平面。
首先我们要先认识一下4种坐标:
- 世界坐标 (World reference system)
- 相机坐标 (camera coordinate)
- 归一化相机坐标 (normalized coordinate)
- 像素坐标 (pixel coordinate)
我们来品一下这张图><。
世界坐标 是我们客观存在的世界,它有自己的固有坐标。在这里我们定义三维空间的三个方向分别为:
例子:
例子1: 长城。它就存在在那里,有它自己的坐标。
例子2: 3d模型。3d模型在计算机中是以点的坐标来存储的,这个坐标代表点在三个方向上的大小,比如一个点,它的存储形式是。这样的点有个,在3dmm中实际上有53215个这样的三维点,这些点组成了基本的人脸3d模型。相机坐标 是从相机的角度去看世界,相机本身是这个坐标系的原点。
在这里我们定义在这个角度的三维空间的三个方向分别为:
例子:
例子1: 小时候我总觉得门前的山特别高,后来长大之后回到老地方,发现这个山也没那么高嘛。山变了吗?山没变,是我看山的角度变了。
例子2: 正所谓【横看成岭侧成峰】,说的也是这回事。归一化相机坐标 物理成像平面。在这里我们可以定义三维空间的三个方向分别为:
原点是相机坐标的轴与物理成像平面的交点。一般取的方向与方向相同,将点在针孔相机模型到物理成像平面的距离统一为,其中为焦距,这就相当于对相机坐标进行归一化。-
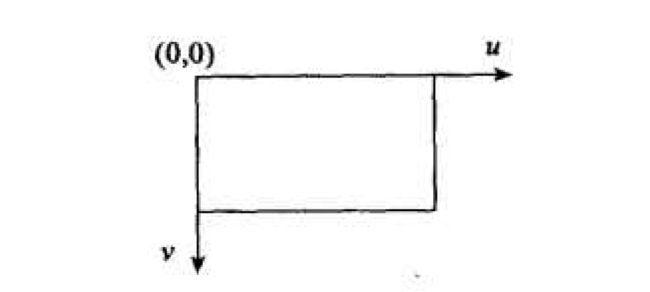
像素坐标 水平方向是U,垂直方向是V,通过这个平面的,二维的UV坐标系。我们可以定位图象上的任意一个像素。
注意 这里的像素坐标的单位是像素,而上述3个坐标系的单位为米。
在这里我们定义二维空间的二个方向分别为:
1.2 计算过程
================== 计算过程(1) 从世界坐标到相机坐标 ==================
已知我们有一个点,它的世界坐标(我们常说的坐标)为:
这个点,它在相机视角下的坐标为:
我们知道和是同一点在不同坐标系下的表达方式,那么和之间是什么关系呢?
这里需要引入一下齐次坐标的概念。
齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示,是指一个用于投影几何里的坐标系统,如同用于欧氏几何里的笛卡儿坐标一般。
比如从欧式坐标变换到齐次坐标时,即:
从齐次坐标变换到欧式坐标时,即:
接下来回到 的变换。
(1)旋转变换
此时:
(2)平移变换
结合(1)(2),那么对于点:
================== 计算过程(2) 从相机坐标到像素坐标 ==================
由图可知:
与相似,那么对于点在相机坐标下的表示 及在归一化相机坐标系里的表现, ():
接下来要从归一化相机坐标系继续变换到像素坐标系,归一化相机坐标系与像素坐标系之间,相差了一个缩放和原点的平移。
我们设像素坐标在轴上缩放了倍,在轴上缩放了倍。同时,原点平移了 ,那么像素坐标系下的与归一化相机坐标系下的的关系为:
我们设, ,得到:
上述内容总结一下,用齐次坐标来表示:
因为齐次坐标乘以非零常数后表达相同含义:
回忆一下的(1)部分的结果:
这里的是齐次坐标,为了将这一部分带入,
我们称这个矩阵为内部参数,
这可以写作 是不是很眼熟,这不是的齐次坐标嘛!
============================== 总结 ==============================
即:
当我们有一个3d模型的n个点的三维坐标,可以通过这个变换得到它的照片。
2. 例子 + 代码
比如我们提到的点,它的世界坐标是。
================== 计算过程(1) 从世界坐标到相机坐标 ==================
(1)旋转变换
此时:
def angle2matrix(angles):
'''
根据右手系三个旋转角,
得到三个旋转矩阵。
Args:
angles: [3,]. x, y, z angles
x: pitch. positive for looking down.
y: yaw. positive for looking left.
z: roll. positive for tilting head right.
Returns:
R: [3, 3]. rotation matrix.
'''
#np.deg2rad将角度变为弧度pi
x, y, z = np.deg2rad(angles[0]), np.deg2rad(angles[1]), np.deg2rad(angles[2])
# x
Rx=np.array([[1, 0, 0],
[0, cos(x), -sin(x)],
[0, sin(x), cos(x)]])
# y
Ry=np.array([[ cos(y), 0, sin(y)],
[ 0, 1, 0],
[-sin(y), 0, cos(y)]])
# z
Rz=np.array([[cos(z), -sin(z), 0],
[sin(z), cos(z), 0],
[ 0, 0, 1]])
R=Rz.dot(Ry.dot(Rx))
return R.astype(np.float32)
(2)平移变换
结合(1)(2),那么对于点:
def similarity_transform(vertices, s, R, t3d):
''' similarity transform. dof = 7.
3D: s*R.dot(X) + t
Homo: M = [[sR, t],[0^T, 1]]. M.dot(X)
Args:(float32)
vertices: [nver, 3].
s: [1,]. scale factor.
R: [3,3]. rotation matrix.
t3d: [3,]. 3d translation vector.
Returns:
transformed vertices: [nver, 3]
'''
t3d = np.squeeze(np.array(t3d, dtype = np.float32))
transformed_vertices = s * vertices.dot(R.T) + t3d[np.newaxis, :]
return transformed_vertices
值得注意的是:函数angle2matrix(angles)中从世界坐标到相机坐标的计算并没有用到齐次坐标。只在欧式坐标下计算,
这并没有关系,因为齐次坐标和非齐次坐标本质上并没有区别:
只要在用的时候区分开就好。
我们之所以引入齐次坐标是为了直接计算。
================== 计算过程(2) 从相机坐标到像素坐标 ==================
我们已经知道:
还原一下这个过程,相机坐标归一化相机坐标像素坐标。
(2.1) 相机坐标归一化相机坐标
我们可以假设物品的深度,远远小于物体与相机间的距离,比如两个点,两个点的方向坐标,此时我们可以直接删去方向坐标,且归一化时我们取:
这样的映射也称为平行映射(orthographic project).
def orthographic_project(vertices):
return vertices.copy()
这里虽然保留,其实我们只取。
(2.2) 归一化相机坐标像素坐标
取归一化相机坐标像素坐标时无缩放, 归一化相机坐标的圆心落在像素为的2d照片的中心,此时在像素坐标系下的坐标为
那么对于点:
def to_image(vertices, h, w):
'''
Args:
vertices: [nver, 3]
h: height of the rendering
w : width of the rendering
Returns:
projected_vertices: [nver, 3]
'''
image_vertices = vertices.copy()
# move to center of image
image_vertices[:,0] = image_vertices[:,0] + w/2
image_vertices[:,1] = image_vertices[:,1] + h/2
# flip vertices along y-axis.
image_vertices[:,1] = h - image_vertices[:,1] - 1
return image_vertices
至此,得到三维点在照片里的像素坐标。