二叉树基础
树(Tree)
树是一种非线性表结构,比线性表的数据结构要复杂的多:
| 树的种类 |
|---|
| 树、二叉树 |
| 二叉查找树 |
| 平衡二叉查找树、红黑树 |
| 递归树 |
“树”的特征
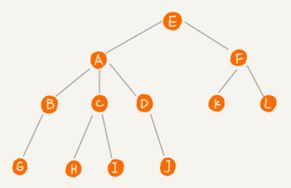
“树”这种数据结构里面每个元素叫做“节点”;用来连接相邻节点之间的关系叫做“父子关系”。
比如下面这幅图,A节点就是B结点的父节点,B节点是A结点的子节点。B、C、D这三个结点的父节点是同一个节点,所以他们之间互称为兄弟节点。没有父节点的节点叫根节点,也就是图中的节点E。没有子节点的节点叫做叶子节点或者叶节点,比如如中的
G、H、I、J、K、L 都是叶子节点。
高度(Height)、深度(depth)、层(Level)的定义:
节点的高度 = 节点到叶子节点的最长路径(边数)
节点的深度 = 根节点到这个节点所经历的边的个数
节点的层数 = 节点的深度 + 1
树的高度 = 根节点的高度
“高度”是从下往上度量,从最底层开始计数,计量的起点是0。
“深度”是从上往下度量,从根节点开始度量计数起点也是0。
“层数”跟深度的计算类似,不过计数起点是1。
二叉树(Binary Tree)
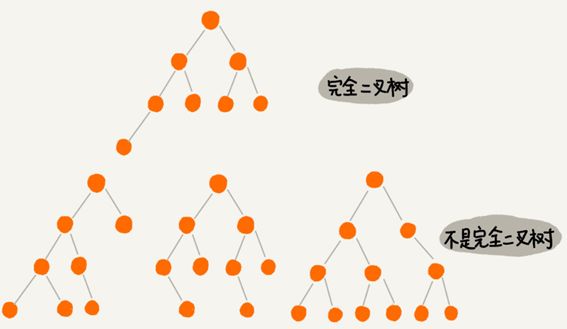
二叉树的每个节点最多有两个子节点,分别是左子节点和右子节点。二叉树中,有两种比较特殊的树,分别是满二叉树和完全二叉树。满二叉树又是完全二叉树的一种特殊情况。
二叉树可以用链式存储,也可以用数组顺序存储。数组顺序存储的方式比较适合完全二叉树,其他类型的二叉树用数组存储会比较浪费存储空间。除此之外,二叉树里非常重要的操作就是前、中、后序遍历操作,遍历的时间复杂度是O(n),需要用递归代码来实现。
二叉树是树的一种,特点是每个节点最多有两个子节点,分别是左子节点和右子节点。
不过,二叉树有的节点只有左子节点,有的节点只有右子节点:
上图编号2的二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫做满二叉树。
编号3的二叉树中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做完全二叉树。
完全二叉树
完全二叉树和非完全二叉树的区别:
最后一层的叶子节点靠左排列的才叫完全二叉树,如果靠右排列就不能叫完全二叉树了。
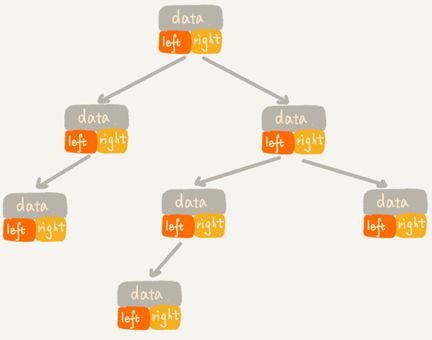
存储一棵树有两种方式,一种是基于指针或者引用的二叉链式存储法,一种是基于数组的顺序存储法。
链式存储法中每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。从根节点开始可以通过左右子节点的指针,把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树都是通过这种结构来实现的。
基于数组的顺序存储法:把根节点存储在下标i = 1的位置,那左子节点存储在下标2 * i的位置,右子节点存储在2 * i + 1 = 3的位置。以此类推,B节点的左子节点存储在2 * i = 2 * 2 = 4的位置,右子节点存储在2 * i + 1 = 2 * 2 + 1 = 5的位置。
如果节点X存储在数组中下标为i的位置,左子节点的下标为2 * i,右子节点为2 * i + 1.反过来,下标为 i / 2的位置存储就是它的父节点。通过这种方式,只要知道根节点存储的位置(一般情况下,为了方便计算子节点,根节点会存储在下标为1的位置),就可以通过下标计算,把整棵树都串起来。
一颗完全二叉树仅仅“浪费”了一个下标为0的存储位置,如果是非完全二叉树,会浪费比较多的数组存储空间。
如果某棵二叉树是一棵完全二叉树,用数组存储无疑是最节省内存的一种方式。因为数组存储方式并不需要存储额外的左右子节点的指针。
堆其实就是一种完全二叉树,最常用的存储方式是数组。
二叉树的遍历
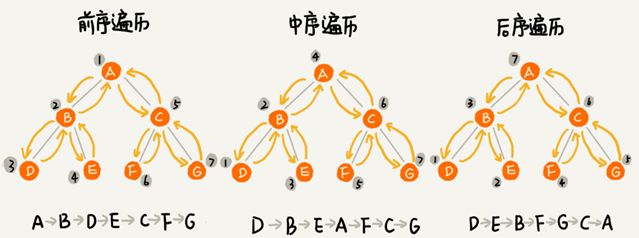
将二叉树所有节点遍历打印出来有三种方式,前序遍历、中序遍历和后序遍历。其中前、中、后序,表示的是节点与它的左右子树节点遍历打印的先后顺序。
- 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历是指,对于书中的任意节点,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
实际上,二叉树的前、中、后序遍历就是一个递归的过程。比如,前序遍历,其实就是先打印根节点,然后再递归打印左子树,最后递归地打印右子树。
写递推公式的关键就是,如果要解决问题A,就假设子问题B、C已经解决,然后再来看如何利用B、C来解决A。前、中、后序遍历的递推公式:
前序遍历的递推公式
preOrder(r) = print r -> preOrder(r -> left) -> preOrder(r -> right)
中序遍历的递推公式
inOrder(r) = inOrder(r -> left) -> print r -> inOrder(r -> right)
后序遍历的递推公式
postOrder(r) = postOrder(p -> left) -> postOrder(r -> right) -> r
java伪代码
void preOrder(Node* root){
if (root == null) return;
print root
preOrder(root -> left);
preOrder(root -> right)
}
void inOrder(Node* root){
if (root == null) return;
inOrder(root -> left);
print root;
inOrder(root -> right);
}
void postOrder(Node* root){
if (root == null) return;
postOrder(root -> left);
psotOrder(root -> right);
print root;
}
二叉树遍历的时间复杂度
遍历过程中每个节点最多会被访问两次,所以遍历操作的时间复杂度跟节点的个数n成正比,二叉树遍历的时间复杂度是O(n)。
按层次遍历二叉树
除了前、中、后序三种二叉树遍历方式外还有按层遍历这种遍历方式。
实现思路:
按照广度优先的遍历算法的思路,引入一个队列,根节点现如队列,然后开始从队列头部取元素,每取一个元素则先打印当前元素,然后依次将左右子节点加入队列,若左子节点或右子节点为空则跳过此步。
python实现代码:
from collections import deque
# 层级遍历
def layer_order(root: TreeNode):
if not root: return
queue = deque([root])
while queue:
e: TreeNode = queue.popleft()
yield e.val
if e.left: queue.append(e.left)
if e.right: queue.append(e.right)
给定一个二叉树,返回其按层次遍历的节点值。(即逐层地,从左到右访问所有节点)
例如:给定二叉树:[3, 20, null, null, 15, 7]
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9, 20]
[15, 7]
]
python代码实现
:
def level_order(root: TreeNode):
levels = []
if not root:
return levels
level = 0
queue = deque([root])
while queue:
levels.append([])
for i in range(len(queue)):
node = queue.popleft()
levels[level].append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
level += 1
return levels
二叉查找树(Binary Search Tree)
二叉查找树是二叉树中最常用的一种类型,也叫二叉搜索树。二叉查找树支持动态数据集合的快速插入、删除、查找操作。
二叉查找树要求,在树中任意一个节点,其左子树中的每个节点的值都小于这个节点的值,而右子树每个节点的值都大于这个节点的值:
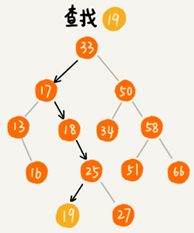
1.二叉查找树的查找操作
先取根节点,如果它等于要查找的数据就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找,如果要查找的数据比根节点的值大,那就在右子树中递归查找。
java代码实现:
public class BinarySearchTree{
private Node tree;
public Node find(int data){
Node p = tree;
while(p != null){
if (data < p.data){
p = p.left;
} else if (data > p.data){
p = p.right;
} else {
return p;
}
}
return null;
}
public static class Node{
private int data;
private Node left;
private Node right
public Node(int data){
this.data data;
}
}
}
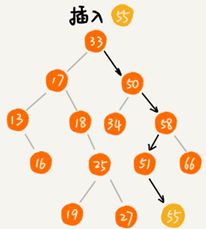
2.二叉查找树的插入操作
二叉查找树的插入过程需要从根节点开始,依次比较要插入的数据和节点的大小关系。
如果要插入的数据比节点的数据大,并且节点的右子树为空,就将数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
java代码实现:
public void insert(int data){
if (tree == null){
tree = new Node(data);
return;
}
Node p = tree;
while(p != null){
if (data > p.data){
if (p.right == null){
p.right = new Node(data);
return;
}
p = p.right;
} else {
if (p.left == null){
p.left = new Node(data);
return;
}
p = p.left;
}
}
}
3.二叉查找树的删除操作
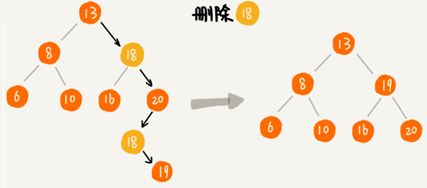
针对要删除节点的子节点个数的不同需要分2中情况来处理。
如果要删除的节点只有一个子节点(只有左子节点或者右子节点)或没有子节点(左右子节点均为null),只需要将要删除的父节点的指针指向要删除节点的子节点。比如下图中删除节点55、13。
如果要删除的节点有两个子节点。需要找到这个节点的右子树的最小节点,把它替换到要删除的节点上。然后再按照上面方法删除掉这个最小节点。比如下图中的删除节点18。(用左子树的最大节点进行替换也可以)
java实现代码:
public void delete(int data){
// p指向要删除的节点,初始化指向根节点
Node p = tree;
// pp记录的是p的父节点
Node pp = null;
while (p != null && p.data != data){
pp = p;
if (data > p.data) {
p = p.right;
} else {
p = p.left;
}
}
// 没有找到
if (p == null){
return;
}
//要删除的节点有两个子节点
if (p.left != null && p.right != null){
//查找右子树中最小的节点
Node minP = p.right;
// minPP表示minP的父节点
Node minPP = p;
while (minP.left != null){
minPP = minP;
minP = p.left;
}
//将minP的数据替换到p中
p.data = minP.data;
//下面就变成了删除minP了
p = minP;
pp = minPP;
}
// 删除节点是叶子节点或者仅有一个子节点
// p的子节点
Node child;
if (p.left != null){
child = p.left;
} else if (p.right != null){
child = p.right;
} else {
child = null;
}
//删除的是根节点
if (pp == null) {
tree = child;
} else if (pp.left = p){
pp.left = child;
} else {
pp.right = child;
}
}
关于二叉查找树的删除操作,最简单的方法是单纯将要删除的节点标记为“已删除”并不真正从树中将这个节点去掉。这样原本删除的节点还需要存储在内存中,缺点是比较浪费内存空间。
4.二叉查找树的其他操作
二叉查找树中还可以支持快速地查找最大节点和最小节点、前驱结点和后继结点。
二叉查找树也叫做二叉排序树,中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是O(n)。
Python代码实现:
def find_min(self) -> Optional[TreeNode]:
if self.tree is Node: return None
p = self.tree
while p.left:
p = p.left
return p
def find_max(self) -> Optional[TreeNode]:
if self.tree is None: return None
p = self.tree
while p.right:
p = p .right
return p
def _in_order(self, root: Optional[TreeNode]):
if root:
yield from self._in_order(root.left)
yield root.data
yield from self._in_order(root.right)
def in_order(self) -> list:
if self.tree is Node:
return []
return list(self._in_order(self.tree))
二叉查找树的Python实现代码
from collections import deque
from typing import Optional, List
class TreeNode:
def __init__(self, data=None):
self.data = data
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self, val_list=None):
if val_list is None:
val_list = []
self.tree: Optional[TreeNode] = None
for n in val_list:
self.insert(n)
def find(self, data):
p = self.tree
while p and p.data != data:
p = p.left if data < p.data else p.right
return p
def insert(self, data):
if not self.tree:
self.tree = TreeNode(data)
return
pp = None
p = self.tree
while p:
pp = p
p = p.left if p.data > data else p.right
if pp.data > data:
pp.left = TreeNode(data)
else:
pp.right = TreeNode(data)
def delete(self, data):
p: Optional[TreeNode] = self.tree # p指向要删除的节点,初始化指向根节点
pp: Optional[TreeNode] = None # pp记录的是p的父节点
while p and p.data != data:
pp = p
p = p.right if p.data < data else p.left
if not p: return # 没有找到
if p.left and p.right: # 查找右子树中最小节点
min_p = p.right # 记录右子树的最小节点
min_pp = p # minPP表示minP的父节点
while min_p.left:
min_pp = min_p
min_p = min_p.left
p.data = min_p.data # 替换数据
p, pp = min_p, min_pp # p指向要删除的min_p
# 删除节点是叶子节点或者仅有一个子节点
child: Optional[TreeNode] = p.left if p.left else p.right
if not pp:
self.tree = child # 删除的是根节点
elif pp.left == p:
pp.left = child
else:
pp.right = child
def find_min(self) -> Optional[TreeNode]:
if self.tree is None: return None
p = self.tree
while p.left:
p = p.left
return p
def find_max(self) -> Optional[TreeNode]:
if self.tree is None: return None
p = self.tree
while p.right:
p = p.right
return p
def _in_order(self, root: Optional[TreeNode]):
if root:
yield from self._in_order(root.left)
yield root.data
yield from self._in_order(root.right)
def in_order(self) -> list:
if self.tree is None:
return []
return list(self._in_order(self.tree))
def __repr__(self):
return str(self.in_order())
def __iter__(self):
return self._in_order(self.tree)
def draw_tree(self):
if not self.tree:
return
# level = 0
queue = deque([self.tree])
while queue:
length = len(queue)
if set(queue) == {None}: return
for i in range(length):
node = queue.popleft()
if node:
print(node.data, end="")
queue.append(node.left)
queue.append(node.right)
else:
print(None, end="")
queue.append(None)
queue.append(None)
if i != length - 1:
print(",", end="")
else:
print()
if __name__ == '__main__':
nums = [4, 2, 10, 6, 1, 7, 3]
bst = BinarySearchTree(nums)
print(bst)
bst.draw_tree()
# 插入
bst.insert(5)
print(bst)
print(bst.find(2).data)
# 删除
bst.delete(6)
print(bst)
bst.delete(4)
print(bst)
bst.draw_tree()
# min max
print(bst.find_max().data)
print(bst.find_min().data)
支持重复数据的二叉查找树
在实际的软件开发中,在二叉查找树中存储的,是一个包含很多字段的对象。利用对象的某个字段作为键值来构建二叉查找树,对象中的其他字段叫做卫星数据。
如果存储的两个对象键值相同的两种解决方法:
二叉查找树中每一个结点存储链表或支持动态扩容的数组,把值相同的数据存储在同一个节点上。
每个节点仍然只存储一个数据。在查找插入位置的过程中,如果碰到了一个节点的值,与要插入数据的值相同,就把这个新插入的数据当作大于这个节点的值来处理,放到这个节点的右子树。
查找数据的时候,遇到值相同的节点并不停止查找操作,而是继续在右子树中查找,直到遇到叶子节点,才停止。这样就可以把键值等于要查找的值的所有节点都找出来。
对于删除操作也需要先查找每个要删除的节点,然后再一次删除。
二叉查找树的时间复杂度分析
二叉查找树的形态各式各样。下图中同一组数据构造的三种二叉查找树,他们的查找、插入、删除操作的执行效率是不一样的。
不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是O(height)。
上图中,第一种二叉查找树,根节点的左右子树极度不平衡,已经退化成了链表,所以查找的时间复杂度就变成了O(n)。
最理想的情况下,二叉查找树是一颗完全二叉树(或满二叉树),插入、删除、查找操作的时间复杂度是O(logn)。
树的高度就等于最大层数减1,包含n个节点的满二叉树中,第一层包含1个节点,第二层包含2个节点,第三层包含4个节点,一次类推,下面一层节点个数是上一层的2倍,第k层包含的节点个数就是2^(k - 1)。
对于完全二叉树来说,最后一层的节点个数在1到2^(k - 1)个之间(假设最大层数是K)。n满足这样一个关系:
1 + 2 + 4 + 8 + ... + 2^(k - 2) + 1 <= n <= 1 + 2 + 4 + 8 + ... + 2^(k - 2) + 2^(k - 1) => 2^(k - 1) <= n <= 2^k - 1 => log(n + 1) <= K <= logn + 1
K的范围是[log(n + 1), logn + 1]。完全二叉树的层数小于等于logn + 1,即高度小于等于logn。
散列表vs二叉查找树
散列表的优势:
三猎豹的插入、删除、查找操作的时间复杂度可以做到常量级的O(1),而二叉查找树在比较平衡的情况下,插入、删除、查找操作的时间复杂度才是O(logn)。
散列表的劣势:
第一,散列表要输出有序的数据,需要先进行排序;二叉查找树只需要中序遍历,就可以在O(n)的时间复杂度内,输出有序的数据序列。
第二,散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定;最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在O(logn)。
第三,因为哈希冲突的存在,散列表的实际查找速度可能不一定比O(logn)快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
第四,散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
最后,为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
综合这几点,平衡二叉查找树在某些方面还是优于散列表的。
求给定二叉树的确切的高度
思路:
递归法,根节点高度 = max(左子树高度,右子树高度) + 1
实现代码:
def get_level(node: TreeNode) -> int:
if node is Node: return 0
return max(get_level(node.left), get_level(node.right)) + 1