完整代码在:https://github.com/nicktming/code/tree/master/data_structure
二叉平衡树
因为如果连续插入已经排好序的键到二叉查找树,二叉查找树相当于变成了一个链表,查找的时间会是
O(n),为了解决这个问题,二叉平衡树应运而生.
bst_1.png
它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
为了达成这个目标,需要通过一些手段也就是旋转来让树平衡.
四种情况
- 对当前节点的左孩子的左子树改变
右旋转- 对当前节点的左孩子的右子树改变
左-右旋转- 对当前节点的右孩子的左子树改变
右-左旋转- 对当前节点的右孩子的右子树改变
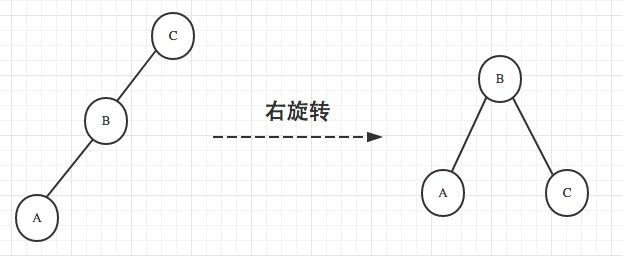
右旋转
接下来一个个来分析
定义一下树结构
public class BinaryBalancedTree, Value> {
private Node root;
private class Node {
Key key;
Value value;
Node left, right;
int height;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
}
public String toString() {
return "[" + key + "," + value + "," + height + "]";
}
}
private int height(Node h) {
return h == null ? -1 : h.height;
}
private int updateHeight(Node h) {
return Math.max(height(h.left), height(h.right)) + 1;
}
}
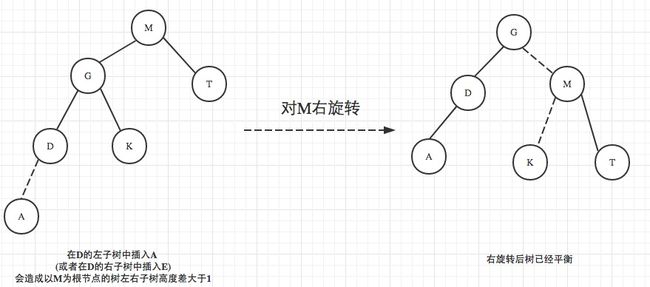
情况1: 右旋转
balancetree_6.jpeg
往平衡树里面增加一个节点,也就是在M的左孩子(G)的左子树(以D为根节点的左子树)中插入一个节点A(或者E),此时M的高度差会从1变化为2,即出现了不平衡. 对M节点进行右旋会使树达到平衡.
balancetree_5.jpeg
/* 右旋 */
private Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
h.height = updateHeight(h);
x.height = updateHeight(x); //h,x顺序不能变
return x;
}
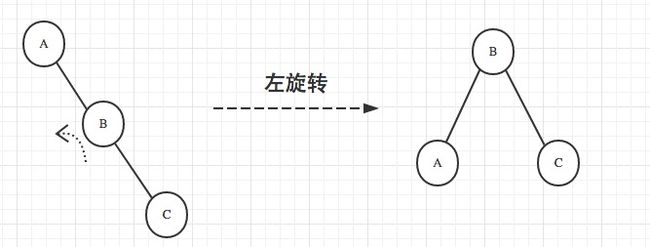
情况4: 左旋
balancetree_7.jpeg
往T的左右子孩子加入一个节点Q(或者X)都会导致G为根节点的左右子树高度差为2出现不平衡,因此需要对G进行左旋转达到平衡.
balancetree_8.jpeg
/* 左旋 */
private Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
h.height = updateHeight(h);
x.height = updateHeight(x); //h,x顺序不能变
return x;
}
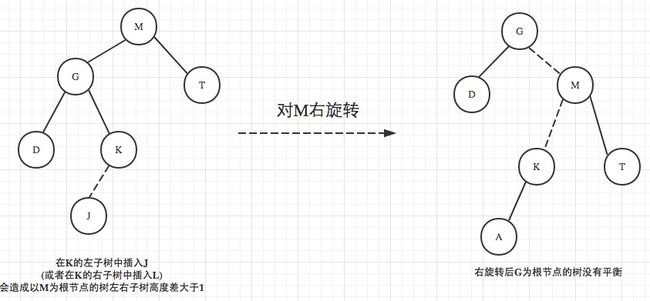
情况2: 左-右旋转
往K的左孩子插入J或者右子树插入L都会使以M为根节点的左右子树高度差为2而出现不平衡,然后通过一次右旋转还是没有达到平衡的效果,左旋转是更加不可能.
原因: 因为右旋转后M的左孩子就是G的右孩子,本来就是因为G的右孩子的高度增加了使得M的左子树高度增加从而比M的右子树高度高了2个长度.因此我们需要把G的右子树的高度转移到G的左子树上面后,这样就相当于G的右子树没有增加了节点,对M进行右旋转的时候就可以了.
仔细体会一下原因
balancetree_9.jpeg
balancetree_10.jpeg
/*左-右旋转*/
private Node rotateLeftRight(Node h) {
h.left = rotateLeft(h.left);
return rotateRight(h);
}
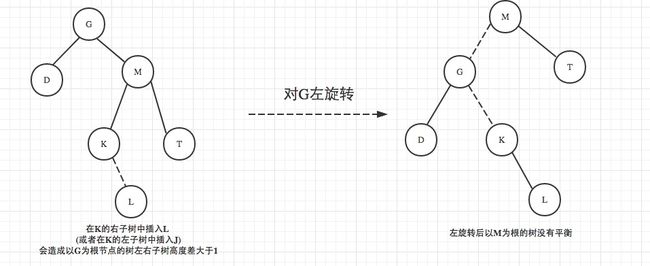
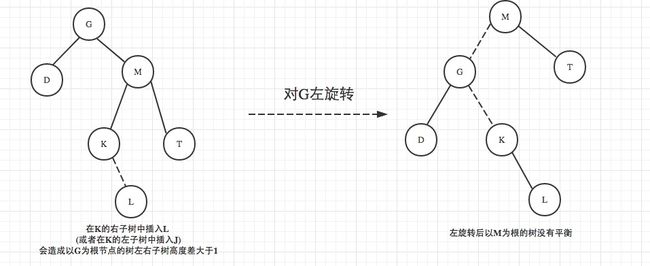
情况3: 右-左旋转
思想与情况2类似,给出图以供思考
balancetree_13.jpeg
balancetree_13.jpeg
/*右-左旋转*/
private Node rotateRightLeft(Node h) {
h.right = rotateRight(h.right);
return rotateLeft(h);
}
插入
进入正题, 如何向二叉平衡树中插入一个节点, 做法与二叉查找树类似(对二叉查找树不了解的可以看一下我的另外一篇博客二叉查找树 Java实现),只是额外增加了平衡的操作. 看代码.
public void put(Key key, Value value) {
root = put(root, key, value);
}
private Node put(Node h, Key key, Value value) {
if (h == null) return new Node(key, value);
int cmp = key.compareTo(h.key);
if (cmp < 0) {
h.left = put(h.left, key, value);
if (height(h.left) - height(h.right) == 2) { //出现不平衡 只会是左子树比右子树高2
if (key.compareTo(h.left.key) < 0) { // h.左孩子的左子树
h = rotateRight(h); //对h进行右旋转
} else {
h = rotateLeftRight(h); // 对h进行左-右旋转
}
}
} else if (cmp > 0) {
h.right = put(h.right, key, value);
if (height(h.right) - height(h.left) == 2) { //出现不平衡 只会是右子树比左子树高2
if (key.compareTo(h.right.key) > 0) { // h.右孩子的右子树
h = rotateLeft(h); //对h进行左旋转
} else {
h = rotateRightLeft(h);
}
}
} else { // 更新value
h.value = value;
}
h.height = updateHeight(h);
return h;
}
balancetree_16.jpeg
对比：
balancetree_15.jpeg
删除
删除也是一样的道理,如果你对二叉查找树的删除比较了解的话,其实理解这个删除操作也会比较简单.
删除最小键
作为预热我们先看一下删除最小键将如何删除.
思路其实是一样的,直接将被删除的节点的右孩子返回给上一层即可.
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node h) {
if (h == null) return null;
if (h.left == null) return h.right;
h.left = deleteMin(h.left);
if (height(h.right) - height(h.left) == 2) {
h = rotateLeft(h);
}
return h;
}
删除任意键
有三种情况:
- 被删除的键只有右孩子
思想与删除最小值很类似- 被删除的键只有左孩子
思想与删除最大值很类似- 被删除的键有左右孩子
把被删除节点的右子树的最小键换到当前节点,然后删除它的右子树的最小键即可
与二叉查找树不同的是每一次都要检查树是否平衡
public Node min(Node h) {
if (h == null) return h;
while (h.left != null) h = h.left;
return h;
}
public void delete (Key key) {
root = delete(root, key);
}
private Node delete(Node h, Key key) {
if (h == null) return null;
int cmp = key.compareTo(h.key);
if (cmp < 0) {
h.left = delete(h.left, key);
if (height(h.right) - height(h.left) == 2) { //出现不平衡 只会是右子树比左子树高2
h = rotateLeft(h);
}
} else if (cmp > 0) {
h.right = delete(h.right, key);
if (height(h.left) - height(h.right) == 2) { //出现不平衡 只会是右子树比左子树高2
h = rotateRight(h);
}
} else {
if (h.left == null) return h.right;
if (h.right == null) return h.left;
Node min = min(h.right);
min.right = deleteMin(h.right);
min.left = h.left;
h = min;
if (height(h.left) - height(h.right) == 2) {
h = rotateRight(h);
}
}
h.height = updateHeight(h);
return h;
}
查找
与二叉查找树一样的算法就不多说了
整体代码
import java.util.LinkedList;
import java.util.Queue;
public class BinaryBalancedTree, Value> {
private Node root;
private class Node {
Key key;
Value value;
Node left, right;
int height;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
}
public String toString() {
return "[" + key + "," + value + "," + height + "]";
}
}
private int height(Node h) {
return h == null ? -1 : h.height;
}
private int updateHeight(Node h) {
return Math.max(height(h.left), height(h.right)) + 1;
}
/* 右旋 */
private Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
h.height = updateHeight(h);
x.height = updateHeight(x); //h,x顺序不能变
return x;
}
/* 左旋 */
private Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
h.height = updateHeight(h);
x.height = updateHeight(x); //h,x顺序不能变
return x;
}
/*左-右旋转*/
private Node rotateLeftRight(Node h) {
h.left = rotateLeft(h.left);
return rotateRight(h);
}
/*右-左旋转*/
private Node rotateRightLeft(Node h) {
h.right = rotateRight(h.right);
return rotateLeft(h);
}
public void put(Key key, Value value) {
root = put(root, key, value);
}
private Node put(Node h, Key key, Value value) {
if (h == null) return new Node(key, value);
int cmp = key.compareTo(h.key);
if (cmp < 0) {
h.left = put(h.left, key, value);
if (height(h.left) - height(h.right) == 2) { //出现不平衡 只会是左子树比右子树高2
if (key.compareTo(h.left.key) < 0) { // h.左孩子的左子树
h = rotateRight(h); //对h进行右旋转
} else {
h = rotateLeftRight(h); // 对h进行左-右旋转
}
}
} else if (cmp > 0) {
h.right = put(h.right, key, value);
if (height(h.right) - height(h.left) == 2) { //出现不平衡 只会是右子树比左子树高2
if (key.compareTo(h.right.key) > 0) { // h.右孩子的右子树
h = rotateLeft(h); //对h进行左旋转
} else {
h = rotateRightLeft(h);
}
}
} else { // 更新value
h.value = value;
}
h.height = updateHeight(h);
return h;
}
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node h) {
if (h == null) return null;
if (h.left == null) return h.right;
h.left = deleteMin(h.left);
if (height(h.right) - height(h.left) == 2) {
h = rotateLeft(h);
}
return h;
}
public Node min(Node h) {
if (h == null) return h;
while (h.left != null) h = h.left;
return h;
}
public void delete (Key key) {
root = delete(root, key);
}
private Node delete(Node h, Key key) {
if (h == null) return null;
int cmp = key.compareTo(h.key);
if (cmp < 0) {
h.left = delete(h.left, key);
if (height(h.right) - height(h.left) == 2) { //出现不平衡 只会是右子树比左子树高2
h = rotateLeft(h);
}
} else if (cmp > 0) {
h.right = delete(h.right, key);
if (height(h.left) - height(h.right) == 2) { //出现不平衡 只会是右子树比左子树高2
h = rotateRight(h);
}
} else {
if (h.left == null) return h.right;
if (h.right == null) return h.left;
Node min = min(h.right);
min.right = deleteMin(h.right);
min.left = h.left;
h = min;
if (height(h.left) - height(h.right) == 2) {
h = rotateRight(h);
}
}
h.height = updateHeight(h);
return h;
}
public Value get(Key key) {
return get(root, key);
}
private Value get(Node h, Key key) {
if (h == null) return null;
int cmp = key.compareTo(h.key);
if (cmp < 0) return get(h.left, key);
else if (cmp > 0) return get(h.right, key);
else return h.value;
}
public void layerTraverse() {
layerTraverse(root);
}
/*
* 横向遍历
*/
private void layerTraverse(Node h) {
if (h == null) return;
Queue queue = new LinkedList();
queue.add(h);
while (!queue.isEmpty()) {
Queue tmp = new LinkedList();
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.print(cur + " ");
if (cur != null) {
tmp.add(cur.left);
tmp.add(cur.right);
}
}
queue = tmp;
System.out.println();
}
}
public static void main(String[] args) {
BinaryBalancedTree bst = new BinaryBalancedTree();
bst.put("A", 0);
bst.put("B", 1);
bst.put("C", 2);
bst.put("D", 3);
bst.put("E", 4);
bst.put("F", 5);
bst.put("G", 6);
bst.layerTraverse();
bst.delete("D");
bst.layerTraverse();
bst.delete("E");
bst.layerTraverse();
bst.delete("F");
bst.layerTraverse();
}
}
balancetree_17.jpeg