1.栈
栈的定义
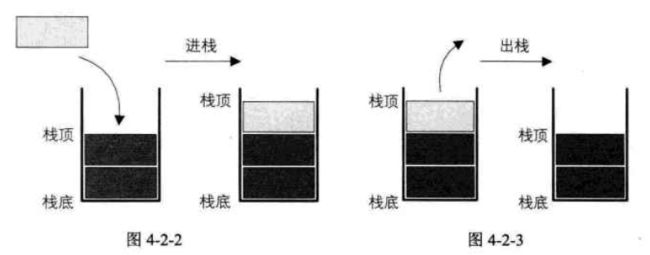
栈是只允许在表尾插入和删除的线性表。
允许插入和删除的一端叫成为栈顶,另一端成为栈底。
后进先出(LIFO)
2.栈的操作
栈的插入称为:进栈,压栈,入栈
栈的删除称为:出栈,弹栈
3.栈的抽象数据类型
ADT 栈
DATA
同线性表。元素具有相同的类型,相邻元素具有前驱和后继的关系。
Operation
InitStack(*S):初始化线性表,建立一个空栈S
DestroyStack(*S):销毁栈
ClearStack(*S):清空栈
IsEmpty(*S):栈是否为空
GetTop(*S,*e):返回栈顶元素,保存在e里
Push(*S,e):入栈
Pop(*S,e):出栈
StackLength(S):返回栈的元素个数
end ADT
4.栈的顺序表实现
/*
ADT 栈
DATA
同线性表。元素具有相同的类型,相邻元素具有前驱和后继的关系。
Operation
InitStack(*S):初始化线性表,建立一个空栈S
DestroyStack(*S):销毁栈
ClearStack(*S):清空栈
IsEmpty(*S):栈是否为空
GetTop(*S,*e):返回栈顶元素,保存在e里
Push(*S,*e):入栈
Pop(*S,e):出栈
StackLength(S):返回栈的元素个数
end ADT
*/
#include
#include
#define MAXSIZE 10
#define OK 1
#define ERROR 0
typedef struct SqStack
{
int data[MAXSIZE];
int top;//指向栈顶 的游标
}SqStack;
//初始化栈
void InitStack(SqStack *S)
{
if(S!=NULL)
S->top = -1;//初始化栈为空
}
//栈是否为空
int IsEmpty(SqStack *S)
{
if(S->top == -1)
{
printf("栈为空\n");
}
else
{
printf("栈不为空\n");
}
return (S->top == -1 ? 1:0);
}
//进栈
int Push(SqStack *S,int e)
{
if(S->top == MAXSIZE - 1)
{
printf("栈满了,无法进栈\n");
return ERROR;
}
S->top++;//移动栈顶游标
S->data[S->top] = e;//进栈
printf("入栈元素为:%d\n",e);
return OK;
}
//出栈
int Pop(SqStack *S,int *e)
{
if(S->top == -1)
{
printf("栈为空,无法出栈\n");
return ERROR;
}
*e = S->data[S->top];
S->top--;
printf("出栈元素为:%d\n",*e);
return OK;
}
//获取栈顶元素
int GetTop(SqStack *S,int *e)
{
if(S->top == -1)
{
printf("栈为空,无法获取栈顶元素\n");
return ERROR;
}
*e = S->data[S->top];
printf("栈顶元素为:%d\n",*e);
return OK;
}
//清空栈
void ClearStack(SqStack *S)
{
if(S!=NULL)
S->top == -1;
}
//销毁栈
void DestroyStack(SqStack *S)
{
S == NULL;
}
//打印栈
void showStack(SqStack *S)
{
while(S->top!=-1)
{
printf("栈的元素为:%d\n",S->data[S->top--]);
}
}
int main()
{
SqStack S;
int e;
InitStack(&S);
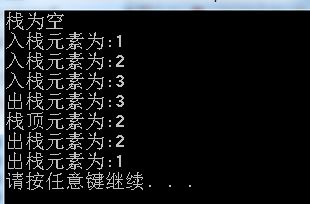
IsEmpty(&S);
Push(&S,1);
Push(&S,2);
Push(&S,3);
Pop(&S,&e);
GetTop(&S,&e);
Pop(&S,&e);
Pop(&S,&e);
system("pause");
return OK;
}
5.栈的链表实现
/*
ADT 栈
DATA
同线性表。元素具有相同的类型,相邻元素具有前驱和后继的关系。
Operation
InitStack(*S):初始化线性表,建立一个空栈S
DestroyStack(*S):销毁栈
ClearStack(*S):清空栈
IsEmpty(*S):栈是否为空
GetTop(*S,*e):返回栈顶元素,保存在e里
Push(*S,*e):入栈
Pop(*S,e):出栈
StackLength(S):返回栈的元素个数
end ADT
*/
#include
#include
#include
#define MAXSIZE 10
#define OK 1
#define ERROR 0
typedef struct Node
{
int data;
struct Node *next;
}Node;//链表节点
typedef struct LinkStack
{
Node *top;//栈顶指针
int count;//栈长度
} LinkStack;//链栈 结构体
//初始化链栈
void initLinkStack(LinkStack *S)
{
S->top = NULL;
S->count = 0;
}
//栈是否为空
int IsEmpty(LinkStack *S)
{
return S->count == 0?1:0;
}
//进栈
int Push(LinkStack *S,int e)
{
Node * p = (Node*)malloc(sizeof(Node));
if(p==NULL)//申请空间失败
return ERROR;
p->data = e;//赋值
p->next = S->top;//指向前一个节点
S->top = p;//指针向上移动一个位置
S->count++;//长度+1
printf("入栈元素为:%d\n",e);
return OK;
}
//出栈
int Pop(LinkStack *S,int *e)
{
Node * p;//用于临时保存栈顶节点
if(IsEmpty(S))
{
printf("栈为空,无法出栈\n");
return ERROR;
}
*e = S->top->data;//保存出栈的元素
p = S->top;//保存栈顶指针指向的节点
S->top = S->top->next;//指向下一个节点
free(p);//释放节点
S->count--;//长度减1
printf("出栈元素为:%d\n",*e);
return OK;
}
//获取栈顶元素
int GetTop(LinkStack *S,int *e)
{
if(S->count == 0)
{
printf("栈为空,无法获取栈顶元素\n");
return ERROR;
}
*e = S->top->data;//获取栈顶元素
printf("栈顶元素为:%d\n",*e);
return OK;
}
int main()
{
int e;
LinkStack S;
initLinkStack(&S);
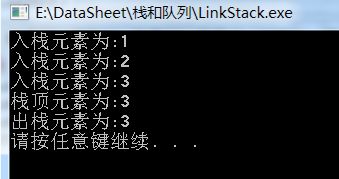
Push(&S,1);
Push(&S,2);
Push(&S,3);
GetTop(&S,&e);
Pop(&S,&e);
system("pause");
return OK;
}
三、栈的应用
A.递归
B.四则运算表达式
1.中缀表达式转换为后缀表达式
例如:
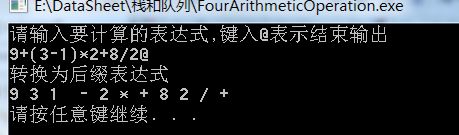
中缀表达式:9+(3-1)*3+10/2
后缀表达式:9 3 1 - 3 * + 10 2 / +
转换规则
实现
该实现有待优化
可以参考自定义结构体的方式实现,会轻松许多!
中缀表达式转后缀表达式 ---- 代码实现
1.输入大于9不能正常识别,因为用的是字符存储
2.有2个小括号也会识别失败
#include
#include
#define MAXSIZE 30
#define OK 1
#define ERROR 0
typedef struct SqStack
{
char data[MAXSIZE];
int top;//指向栈顶 的游标
}SqStack;
//初始化栈
void InitStack(SqStack *S)
{
if(S!=NULL)
S->top = -1;//初始化栈为空
}
//栈是否为空
int IsEmpty(SqStack *S)
{
return (S->top == -1 ? 1:0);
}
//进栈
char Push(SqStack *S,char e)
{
if(S->top == MAXSIZE - 1)
{
printf("栈满了,无法进栈\n");
return ERROR;
}
S->top++;//移动栈顶游标
S->data[S->top] = e;//进栈
//printf("进栈元素为:%c\n",e);
return OK;
}
//出栈
char Pop(SqStack *S)
{
if(S->top == -1)
{
printf("栈为空,无法出栈\n");
return ERROR;
}
return S->data[S->top--];
}
//获取栈顶元素
char GetTop(SqStack *S)
{
if(S->top == -1)
{
printf("栈为空,无法获取栈顶元素\n");
return ERROR;
}
return S->data[S->top];
}
//清空栈
void ClearStack(SqStack *S)
{
if(S!=NULL)
S->top == -1;
}
//销毁栈
void DestroyStack(SqStack *S)
{
S == NULL;
}
//打印栈
void showStack(SqStack *S)
{
while(S->top!=-1)
{
printf("栈的元素为:%c\n",S->data[S->top--]);
}
}
//中缀表达式转换为后缀表达式
void Mid2Last(SqStack *S,char *arr)
{
int i;
printf("转换为后缀表达式\n");
for(i=0;arr[i]!='@';i++)
{
//如果是数字,直接输入
if('0'<=arr[i] && arr[i]<='9')
{
printf("%c ",arr[i]);
}
else if(
arr[i]=='*'
|| arr[i]=='/'
|| arr[i]=='+'
|| arr[i]=='-'
|| arr[i]=='('
|| arr[i]==')'
)
{
if(IsEmpty(S))//如果栈为空,直接入栈
Push(S,arr[i]);
else//否则 取出栈顶元素做优先级比较
{
if(arr[i]=='(')//遇到左括号 直接入栈
Push(S,arr[i]);
else if(arr[i] == ')')//遇到右括号 则栈顶元素依次出栈并输出
{
while(GetTop(S)!='(')//栈顶不等于(括号
{
printf(" %c ",Pop(S));//出栈 并且打印
}
S->top--;//左括号也出栈但是不打印
}
else if(
(arr[i]=='+' || arr[i]=='-') //如果当前元素优先级小于栈顶元素
&& (GetTop(S)=='*'||GetTop(S)=='/'))
{
while(!IsEmpty(S))
printf("%c ",Pop(S));//全部出栈 并且打印
Push(S,arr[i]);//当前元素进栈
}
else
Push(S,arr[i]);//当前元素进栈
}
}
}
while(!IsEmpty(S))//到达表达式末尾
printf("%c ",Pop(S));//全部出栈 并且打印
printf("\n");
}
int main()
{
SqStack S;
int e,i;
char arr[30]={0};
printf("请输入要计算的表达式,键入@表示结束输出\n");
scanf("%s",arr);
InitStack(&S);//初始化栈
Mid2Last(&S,arr); //中缀表达式转为后缀表达式
system("pause");
return OK;
}
结果
1.成功情况
1.失败情况
2.后缀表达式的计算
计算规则