今天刷题,又遇到了二叉树最近公共祖先问题,发现前段时间写的忘光了,因此决定写下来记录一下。
二叉树最近公共祖先,leetcode上涉及题目
面试题68-2 二叉树的最近公共祖先 (同算法题236)
面试题68-1 二叉搜索树的最近公共祖先 (同算法题235)
算法题1123 最深叶结点的最近公共祖先
面试题04.08 首个共同祖先(其实同第一项)
面试题68-2 二叉树的最近公共祖先(算法题236)
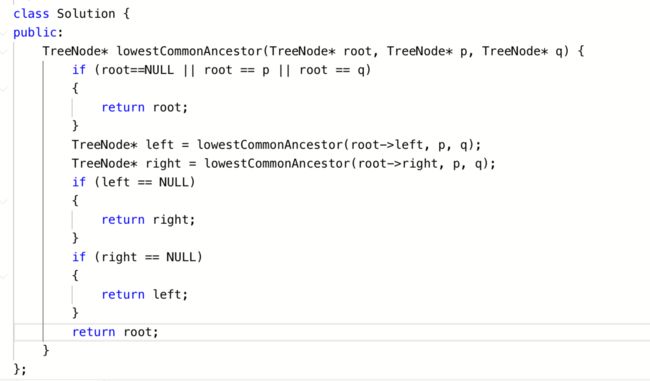
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof
解题思路:
考虑是二叉树,基本就是递归了
1.如果root是null或者root为p或者q结点,则返回root即可
2.在左子树和右子树中分别找p和q的公共祖先,如果其中一个返回为null,说明p和q都在另一个子树中,则公共祖先为另一个子树找到的结点
3.如果两个子树的返回都不是null,说明p和q分别在两个子树中,返回root
c++代码(并没有考虑p或者q不存在的情况)
面试题68-1 二叉搜索树的最近公共祖先 (算法题235)
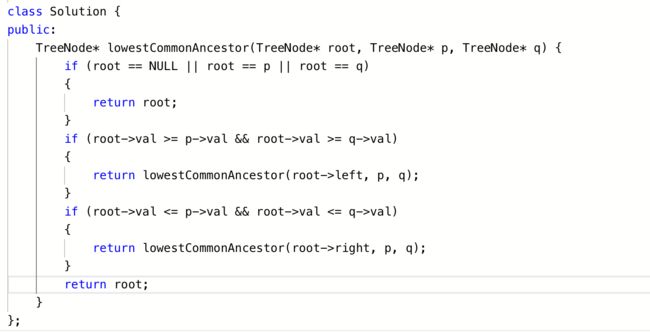
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof
思路:
本题相对于上一题进阶点为二叉树变成了搜索二叉树,搜索二叉树有两个常用特点:1.查找时可判断查找val与结点val大小,若小于当前结点val,则在左子树中查找,若大于,则在右子树中查找 2.搜索二叉树的中序遍历为有序递增数组
1.同上题,如果root为null或root为p或者q,直接返回root
2.如果p和q都小于当前结点val,则搜索左子树即可,若p和q都大于当前结点val,则搜索右子树即可,若一个大一个小,则返回当前结点
c++代码
算法题1123 最深叶结点的最近公共祖先
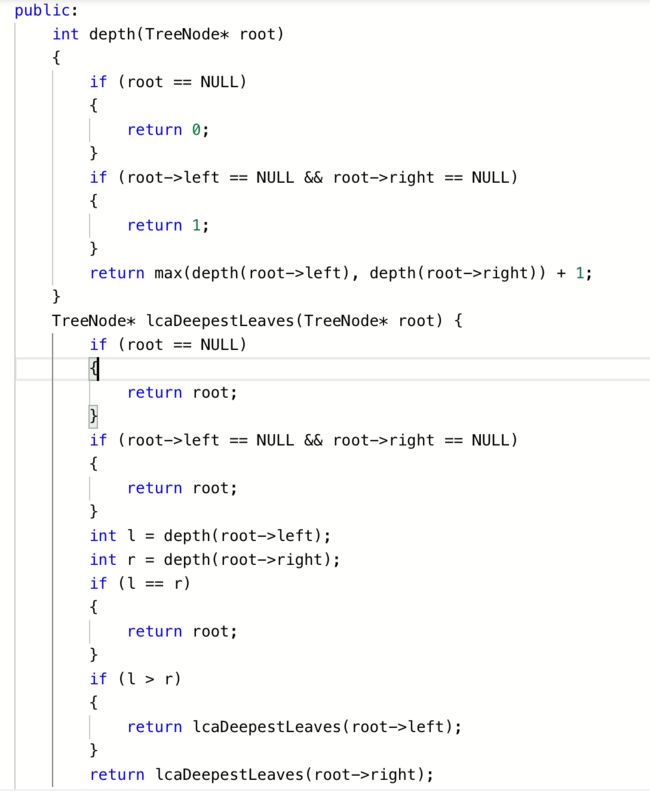
给你一个有根节点的二叉树,找到它最深的叶节点的最近公共祖先。
回想一下:
叶节点 是二叉树中没有子节点的节点
树的根节点的 深度 为 0,如果某一节点的深度为 d,那它的子节点的深度就是 d+1
如果我们假定 A 是一组节点 S 的 最近公共祖先,S 中的每个节点都在以 A 为根节点的子树中,且 A 的深度达到此条件下可能的最大值。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/lowest-common-ancestor-of-deepest-leaves
思路:
当然,可以暴力找到最深的子结点,然后两个找祖先,之后再依次找到当前公共祖先和下一个结点的最近公共祖先
但是这道题有个比较清奇的思路,考虑当前结点的左子树深度大于右子树深度,则要在左子树中寻找。如果右子树大于左子树深度,则在右子树中寻找。如果左子树和右子树深度相同,返回当前结点。
1.如果当前结点为空或当前结点为叶子结点,返回当前结点
2.若当前结点左子树深度大于右子树深度,递归左子树,若深度相同,返回当前结点,否则,递归右子树
面试题04.08 首个共同祖先
设计并实现一个算法,找出二叉树中某两个节点的第一个共同祖先。不得将其他的节点存储在另外的数据结构中。注意:这不一定是二叉搜索树。
思路:同第一道题