前情回顾:
Gephi网络图极简教程
Network在单细胞转录组数据分析中的应用
Gephi网络图极简教程
Network在单细胞转录组数据分析中的应用
网络数据统计分析笔记|| 为什么研究网络
网络数据统计分析笔记|| 操作网络数据
网络数据统计分析笔记|| 网络数据可视化
网络数据统计分析笔记|| 网络数据的描述性分析
网络数据统计分析笔记||网络图的数学模型
单细胞数据以高纬度著称,一则来自测得细胞多,一则来自测得基因也很多。在我们的文章Network在单细胞转录组数据分析中的应用中提到用网络分析工具来解释细胞和基因异质性。网络既是一种数据结构,也是一个模型。Network在高维数据中的应用是多方面的:从可视化到网络拓扑推断。
今天我们就用刚学的热乎的Network知识探索一下我们的单细胞转录组数据吧。核心在找到细胞类型特异(cell-type specific)的某某,对它展开描述。
library(tidyverse)
library(Seurat)
library(SeuratData)
library(psych)
library(qgraph)
library(igraph)
pbmc3k.final
An object of class Seurat
13714 features across 2638 samples within 1 assay
Active assay: RNA (13714 features, 2000 variable features)
2 dimensional reductions calculated: pca, umap
head([email protected])
orig.ident nCount_RNA nFeature_RNA seurat_annotations percent.mt RNA_snn_res.0.5
AAACATACAACCAC pbmc3k 2419 779 Memory CD4 T 3.0177759 1
AAACATTGAGCTAC pbmc3k 4903 1352 B 3.7935958 3
AAACATTGATCAGC pbmc3k 3147 1129 Memory CD4 T 0.8897363 1
AAACCGTGCTTCCG pbmc3k 2639 960 CD14+ Mono 1.7430845 2
AAACCGTGTATGCG pbmc3k 980 521 NK 1.2244898 6
AAACGCACTGGTAC pbmc3k 2163 781 Memory CD4 T 1.6643551 1
seurat_clusters
AAACATACAACCAC 1
AAACATTGAGCTAC 3
AAACATTGATCAGC 1
AAACCGTGCTTCCG 2
AAACCGTGTATGCG 6
AAACGCACTGGTAC 1
table(Idents(pbmc3k.final))
Naive CD4 T Memory CD4 T CD14+ Mono B CD8 T FCGR3A+ Mono NK DC
697 483 480 344 271 162 155 32
Platelet
14
计算每个亚群的差异基因。
mk <- FindAllMarkers(pbmc3k.final)
head(mk)
计算top 20 差异基因的平均表达量,构建们细胞类型特异基因相关性网络。当然你要是能找到每个细胞亚群的有意思的基因集,那故事性要比差异基因强的多了。
genes <- mk %>% group_by(cluster) %>% top_n(20,avg_logFC)
genes<- genes$gene
aver<- AverageExpression(pbmc3k.final,features = unique(genes))
计算相关性
df <- t(aver$RNA)
rownames(df)
corr <- corr.test(df)
设置分组信息。
geneMY <- lapply(names(table(Idents(pbmc3k.final))), FUN = function(x){mk %>%filter( cluster == x ) %>% top_n(20,avg_logFC) -> gene;
genes<- gene$gene
which(colnames(corr$r) %in%genes )})
names(geneMY) <- names(table(Idents(pbmc3k.final)))
pbmc3k_net <- qgraph(corr$r,groups = geneMY,threshold = .1,minimum=.6,label.norm = "AAAAAAA")
绿色表示正相关,红色表示负相关。这时候可以讲一下几个一亚群内部的相关性规律,再提一下亚群间的几个关键的基因,如和别的细胞类型关联较多的基因,为什么?
图的基本性质
pbmc_cent <- centrality_auto(pbmc3k_net)
pbmc_node_cent <- as_tibble(pbmc_cent$node.centrality, rownames = "item")
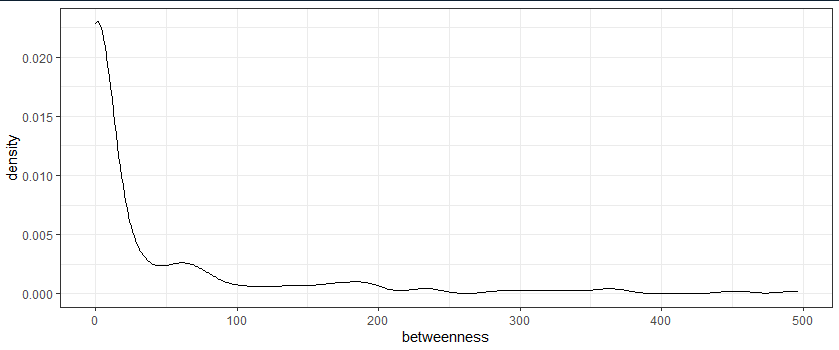
psych::describe(pbmc_node_cent$Betweenness)
vars n mean sd median trimmed mad min max range skew kurtosis se
X1 1 149 44.34 90.95 1 21.49 1.48 0 496 496 2.76 7.91 7.45
# turn it into a tibble
as_tibble(pbmc_node_cent$Betweenness) %>%
# it's calling the variable value by default, so we'll rename it
rename(betweenness = value) %>%
# pass that to ggplot
ggplot(aes(x = betweenness))+
# let's see a density plot
geom_density() + theme_bw()
pbmc3k_net %>% as.igraph() -> cg1
is.weighted(cg1)
[1] TRUE
head(E(cg1)$weight)
[1] -0.1001239 -0.1002145 -0.1003801 -0.1003982 0.1004146 -0.1004702
tail(E(cg1)$weight)
[1] 0.9999990 0.9999991 0.9999992 0.9999993 0.9999995 0.9999998
vcount(cg1)
[1] 149
length(V(cg1))
[1] 149
E(cg1)$weight <- abs(E(cg1)$weight)
as_adjacency_matrix(cg1) -> igraph
igraph <- network::as.network.matrix(igraph)
nodes_num <- length(V(cg1))
nodes_num
vcount(yeast)
edges_num <- length(E(cg1))
edges_num
#平均度(average degree)
average_degree <- mean(degree(cg1))
#或者,2x边数量/节点数量
average_degree <- 2*edges_num/nodes_num
average_degree
#平均加权度(average weighted degree),仅适用于含权网络
#average_weight_degree <- mean(strength(igraph))
#节点和边连通度(connectivity)
nodes_connectivity <- vertex.connectivity(cg1)
nodes_connectivity
edges_connectivity <- edge.connectivity(cg1)
edges_connectivity
#平均路径长度(average path length)
average_path_length <- average.path.length(cg1, directed = FALSE)
average_path_length
#网络直径(diameter)
graph_diameter <- diameter(cg1, directed = FALSE)
graph_diameter
#图密度(density)
graph_density <- graph.density(cg1)
graph_density
#聚类系数(clustering coefficient)
clustering_coefficient <- transitivity(cg1)
clustering_coefficient
#介数中心性(betweenness centralization)
betweenness_centralization <- centralization.betweenness(cg1)$centralization
betweenness_centralization
#度中心性(degree centralization)
degree_centralization <- centralization.degree(cg1)$centralization
degree_centralization
#模块性(modularity),详见 ?cluster_fast_greedy,?modularity,有多种模型
fc <- cluster_fast_greedy(cg1)
modularity <- modularity(cg1, membership(fc))
#互惠性(reciprocity),仅适用于有向网络
#reciprocity(igraph, mode = 'default')
#reciprocity(igraph, mode = 'ratio')
#选择部分做个汇总输出
igraph_character <- data.frame(
nodes_num, #节点数量(number of nodes)
edges_num, #边数量(number of edges)
average_degree, #平均度(average degree)
nodes_connectivity, #节点连通度(vertex connectivity)
edges_connectivity, #边连通度(edges connectivity)
average_path_length, #平均路径长度(average path length)
graph_diameter, #网络直径(diameter)
graph_density, #图密度(density)
clustering_coefficient, #聚类系数(clustering coefficient)
betweenness_centralization, #介数中心性(betweenness centralization)
degree_centralization, #度中心性
modularity #模块性(modularity)
)
igraph_character %>%
knitr::kable(caption = " Descriptives")
Table: Descriptives
| nodes_num| edges_num| average_degree| nodes_connectivity| edges_connectivity| average_path_length| graph_diameter| graph_density| clustering_coefficient| betweenness_centralization| degree_centralization| modularity|
|---------:|---------:|--------------:|------------------:|------------------:|-------------------:|--------------:|-------------:|----------------------:|--------------------------:|---------------------:|----------:|
| 149| 9921| 133.1678| 104| 104| 1.100218| 0.454341| 0.8997823| 0.9058516| 0.0002225| 0.0934609| 0.0159255|
评估社团数量
nv <- vcount(cg1)
ne <- ecount(cg1)
degs <- degree(cg1)
# CHUNK 27
ntrials <- 1000
# CHUNK 28
num.comm.rg <- numeric(ntrials)
for(i in (1:ntrials)){
g.rg <- sample_gnm(nv, ne)
c.rg <- cluster_fast_greedy(g.rg)
num.comm.rg[i] <- length(c.rg)
}
# CHUNK 29
num.comm.grg <- numeric(ntrials)
for(i in (1:ntrials)){
g.grg <- sample_degseq(degs, method="vl")
c.grg <- cluster_fast_greedy(g.grg)
num.comm.grg[i] <- length(c.grg)
}
rslts <- c(num.comm.rg,num.comm.grg)
indx <- c(rep(0, ntrials), rep(1, ntrials))
counts <- table(indx, rslts)/ntrials
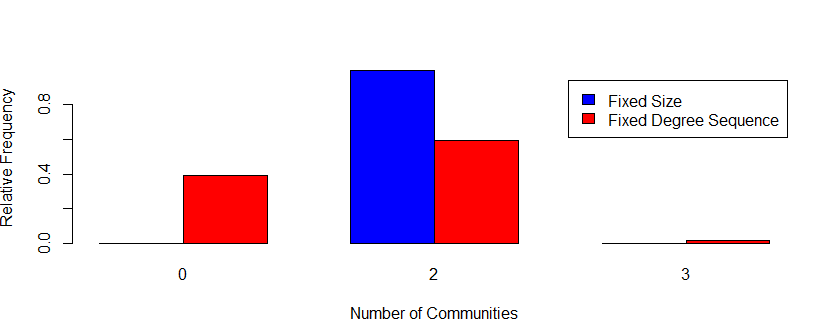
barplot(counts, beside=TRUE, col=c("blue", "red"),
xlab="Number of Communities",
ylab="Relative Frequency",
legend=c("Fixed Size", "Fixed Degree Sequence"))
E(cg1)$weight <- abs(E(cg1)$weight)
length(cluster_fast_greedy(cg1))
[1] 4
社团大于模拟的随机图数量(上异常),说明我们细胞类型特异基因相关性网络是不同寻常的。
评估网络小世界性
ntrials <- 1000
nv <- vcount(cg1)
ne <- ecount(cg1)
cl.rg <- numeric(ntrials)
apl.rg <- numeric(ntrials)
for (i in (1:ntrials)) {
g.rg <- sample_gnm(nv, ne, directed=TRUE)
cl.rg[i] <- transitivity(g.rg)
apl.rg[i] <- mean_distance(g.rg)
}
#
# df <- data.frame(cl.rg = cl.rg,apl.rg = apl.rg)
# head(df %>% reshape2::melt())
# df %>% reshape2::melt() %>% ggplot(aes(factor(variable),value)) + geom_violin() +theme_bw()
summary(cl.rg)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.6901 0.6958 0.6974 0.6974 0.6991 0.7055
ntrials <- 1000
summary(cl.rg)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.6901 0.6958 0.6974 0.6974 0.6991 0.7055
transitivity(cg1)
[1] 0.9058516
mean_distance(cg1)
[1] 1.100218
0.9058516 > 0.7055 小世界性也是有的。
接下来,我们可以把某个子图挖出来仔细看引起这种特异的内在因素,也就是找到了某个基因集,然后又是一波建模和验证。把这篇文章整整就是一篇SCI啊。
如何以细胞而不是以基因来构建网络呢?
可以基于网络推测细胞类型之间的关系,随着单细胞组学的完善,每个细胞都可以测到多个属性,这样就可以类比人类社会的研究方法了。有一门学科,叫做:
到那时,我们可以描述细胞之间的聚集,分离,迁移,交流。细胞之间的调节网络将会在我们面前铺展开来。
https://robchavez.github.io/datascience_gallery/html_only/network_analysis.html#example_2:_correlation_network
https://www.r-graph-gallery.com/250-correlation-network-with-igraph.html