前言
在三维空间中,为了指定一个刚体的位置和姿态,至少需要6个数。本章通过一个附着到物体上的参考坐标系来描述它的位置和姿态。这个坐标系相对于固定坐标系的构型通过一个4x4的矩阵描述。这个矩阵是C-space的隐式表达:刚体的6维C-space空间通过对16维的矩阵施加10个约束获得。
这样的一个矩阵不仅可以表示坐标系的构型,还可以用来:
- 移动或旋转一个向量/坐标系
- 将一个向量/坐标系的描述从一个坐标系转换到另一个坐标系
通过选择用4x4矩阵来表达构型,以上这些操作就可以由简单的线性代数理论完成。这也是为什么我们选择用矩阵表达构型的原因。
任意一个刚体的构型都可以通过从固定参考坐标系出发,对一个恒定的速度(twist)积分指定的时间得到。这种运动类似于螺旋运动(screw motion):围绕一个固定的轴旋转并沿着该轴作平移运动。基于此,我们可以通过6个参数描述的指数坐标(exponential coordinates)来表达构型。这6个参数可以分为:描述螺旋轴方向的参数和一个沿着该轴运动路程的标量参数。
1.1 平面上的刚体运动
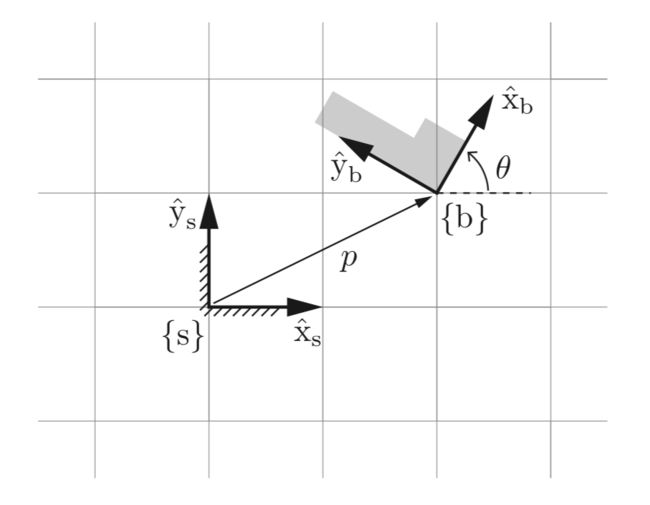
考虑图1中的平面物体,其运动被限制在平面中。图中参考坐标系为固定不动的坐标系,,为坐标轴单位向量,,附着在这个平面物体上,随着物体运动而运动,我们称该坐标系为载体坐标系(body frame),用来表示。
为了描述这个平面物体的构型,只需要指定相对于的位置和姿态。的原点可通过的坐标轴表达:
在确定参考坐标系的情况下,也可以将向量简单的记为。
描述相对于的姿态最简单的方式就是指定一个旋转角度。另一种方法是指定,相对于,的方向:
看起来上面的表达式似乎不是一个很好的用于表达姿态的方法,但是想象一下这个物体在三维空间中任意运动,一个角度将不足以描述坐标系的姿态。实际上我们需要三个角度,但目前为止我们还不清楚如何定义这样一组角度。而将 的坐标轴用 坐标轴的系数来表达却是很直接的一种方式。
正如点 P 可以表达为一个列向量:
,也可以写作两个列向量,组合成一个2x2 的矩阵
矩阵是一个旋转矩阵,尽管包含4个数字,但它们受到3个约束:每一列是单位向量,且两列互相垂直。剩余的一个自由度由来参数化。
综上,将和合并表达为,可作为坐标系相对于的位置和姿态的一种表达。
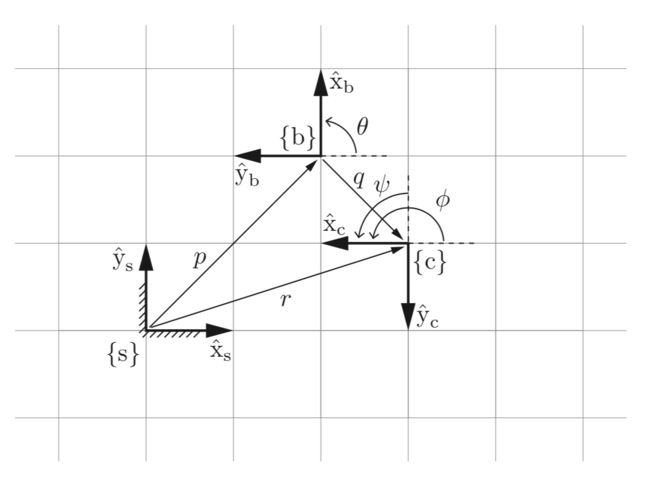
如图2,将在中表达,得到:
同样地,我们也能够在中表达:
如果我们知道了(相对于的构型),(相对于的构型),那么我们可以计算出相对于的构型:
因此不仅可以作为在中的构型表达,还能够将一个点或坐标系从坐标变换到坐标。
考虑图3中的一个刚体,坐标系和固定在它上面。初始状态时,和重合,在中的表达为。而后物体移动,使得与重合,在中的描述为。记的构型为,可验证下面的关系式成立:
与之前的公式很类似,不同点在于这里的 和 都是在下表达的。因此这个表达式不是用于改变坐标,而是用作刚体位移(rigid-body displacement)。图3中发生的变换是:(1)根据转动. (2) 根据移动。
综上,一个旋转矩阵-向量对 有3个作用:
- 表示一个刚体在中的构型
- 改变一个向量或坐标系的参考坐标系
- 移动一个向量或坐标系
注意到图3(a)中的先旋转和移动的刚体位移可以直接通过绕一个图3(b)中的固定点旋转角度完成。这是螺旋运动(screw motion)在平面上的特例。因此,这个位移可以由3个螺旋坐标描述:。其中代表点s在坐标系的坐标(螺旋轴指向纸面朝外)。
另一种表示螺旋运动的方式是将位移看作是以一定的角速度和线速度运动一段距离后产生。观察图3(b),绕s点以一个单位角速度旋转,意味着在点坐标系原点处物体上的一点线速度为。我们可以将这三个数组合起来用一个向量来表示,这是螺旋轴的一种表达。绕该螺旋轴运动一个距离将产生最终的位移。因此可以用三个坐标来表达该物体的位移,我们称它为平面上的刚体位移指数坐标(exponential coordinates)。
角速度和线速度统称为twist,将螺旋轴乘以某个旋转速度得到速度。绕螺旋轴旋转产生的位移和以速度绕螺旋轴旋转一个单位时间得到的位移是相等的,因此也可以被看作是一组指数坐标。
1.2 旋转和角速度
1.2.1 旋转矩阵
旋转矩阵的9个参数受到6个约束,只有3个独立参数。注意到矩阵�的三列对应的是载体坐标系的三个坐标轴,因此矩阵�需满足以下三个条件:
- 单位模长条件:都是单位向量
- 正交条件:
这六个约束可以用一个关系式表达:
所有3x3旋转矩阵构成的集合称为特殊正交群(special orthogonal group),用符号表示。和平面情况一样,一个旋转矩阵有以下三个作用:
- 表示一个旋转
- 改变一个向量或坐标系的参考坐标系
- 旋转一个向量或坐标系
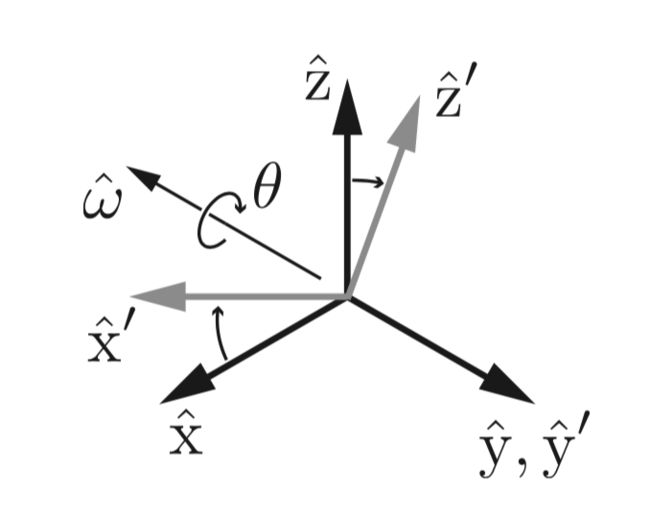
这里重点解释一下第三个作用旋转一个向量或坐标系。如图4,初始状态下,坐标系和重合,坐标轴为,如果我们让绕着某个轴旋转角度,则会得到一个新的坐标系,其坐标轴为。令旋转矩阵表示相对于的旋转,那么就可以将看成一个旋转算子,而不是一个姿态表达,我们可以写作:
这个旋转算子将单位旋转矩阵旋转至。
绕坐标轴的旋转矩阵如下:
更一般地,对于,
其中,,。任意的都可以由单位矩阵绕某个旋转某个获得。注意一个特性,。
假设代表坐标系相对于的旋转,现在我们想让绕单位向量�旋转角度,该旋转由旋转矩阵表示。为了更清楚的表达该旋转,我们还需要指明旋转轴是在中还是中 表达。令坐标系为绕�旋转角度得到(在固定坐标系中描述),为绕�旋转角度得到(在载体坐标系中描述)。这两个新的坐标系可以通过下面的表达式计算出来:
也就是说,前乘一个矩阵代表绕固定坐标系中的旋转,后乘代表绕载体坐标系中的旋转。如果对一个向量旋转,由于只涉及到所在的坐标系,那么也是在该坐标系中描述的,旋转后的向量。
1.2.2 角速度
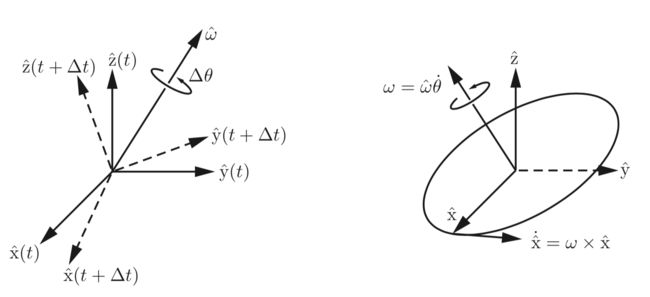
如图5,假设一个旋转的物体上固连着一个坐标系,其坐标轴单位向量为,现在来求取这三个单位坐标轴对时间的导数。注意坐标轴的长度是不变的,只有方向会发生变化。研究载体坐标系在和时刻的姿态的变化,这个变化可以描述为绕过原点的某个轴旋转角度得到。注意这个目前还没有指明在哪个坐标系中描述。
当趋于0时,就变为了旋转的速度,就是瞬时旋转轴。我们可以将和结合起来表示为 角速度 (angular velocity):
参考图5(b),可得到:
为了以坐标形式表达这三个关系式,我们需要选定一个参考坐标系。理论上可以选择任意坐标系,两个很自然的选择是固定坐标系和载体坐标系。
首先选择为参考坐标系。令旋转矩阵表示载体坐标系在时刻时相对于固定坐标系的姿态,是其时间变化率,的第一列描述了轴在固定坐标系下的坐标,和分别为和轴在固定坐标系下的坐标。在某个时刻处,令为角速度在固定坐标系下的表达,则上面的三个关系式可以写为:
这三个关系式可写成矩阵形式:
为了消除右侧的叉乘符号,我们引入一个新的表示符号,将 写为,其中为的反对称(skew-symmetric)矩阵表达:
给定一个向量,定义矩阵为的反对称矩阵表达,即:
所有实反对称矩阵构成的集合叫做(李代数),它包含了当时,所有可能的。
反对称矩阵一个有用的特性如下:给定任意的和,有以下关系式恒成立:
有了新的符号[],旋转矩阵的导数就可以写为:
两边同乘以 ,可得到:
现在我们将表达在坐标系中,记为。注意和是同一个角速度在不同坐标系下的向量表达,由下标消除法则,,因此
将上面的关系式表达为反对称矩阵形式:
综上,有两个关系式将和同角速度联系起来:
需要注意两点:
- 并不是相对于正在运动的坐标系来描述的,而是相对于一个静止坐标系描述,这个静止坐标系同固结在运动物体上的某个坐标系在这一瞬时重合。
- 不依赖于载体坐标系的选择,不依赖于固定坐标系的选择。表面上看,它们都依赖于和,实际上的乘积独立于,的乘积独立于。
1.2.3 旋转的指数坐标表示法
指数坐标(Exponential Coordinates)是旋转的一种三参数表达法。指数坐标用表示,其中是旋转轴单位向量,是旋转角度。如果分开写,就变为了旋转的角-轴(axis-angle)表达法。
旋转矩阵对应的指数坐标可作如下的解读:
- 旋转轴和旋转角度,某一个坐标系初始状态同重合,绕旋转角度,得到的坐标系相对于的姿态可用旋转矩阵表达
- 在中描述的一个角速度,某一个坐标系初始状态同重合,沿着运动单位时间(对在这段时间内积分),得到的坐标系相对于的姿态可用旋转矩阵表达
- 在中描述的一个角速度,某一个坐标系初始状态同重合,沿着运动时间(对在这段时间内积分),得到的坐标系相对于的姿态可用旋转矩阵表达
后两种解读方式暗示我们可以用线性微分方程形式来看待指数坐标。先了解一下向量形式线性微分方程的一些结论:
设线性微分方程为,初始条件为,为常矩阵,。那么该方程的解为:
其中称为矩阵指数(matrix exponential):
还满足下面的特性:
- 如果可以写为且可逆,则
- 如果,则(可以展开后验证)
- (在上面表达式中令可验证)
如图6,假设一个三维向量绕旋转至,可以想象一下这个旋转过程:以一个恒定速度1从旋转到,令 表示向量头部走过的路径,其速度为:
上面的方程是一个线性微分方程,其解为:
由于和是可交换的,上式可写为:
从上式可看出的一个作用,它可以将旋转至 ,对应绕逆时针旋转,则顺时针旋转。
对按照定义展开得到:
由,上式可化简为:
由和的级数展开式可得:
上式称为罗德里格旋转公式(Rodrigues’ formula)。
以上,展示了如何通过矩阵指数,从和创建旋转矩阵。如前所述,的一个作用,它可以将一个向量旋转至 ,同样的,矩阵由三个列向量构成,那么旋转矩阵就是由绕固定坐标系的旋转角度获得。旋转矩阵就是由绕载体坐标系的旋转角度获得。
下面我们将证明,对于任意的旋转矩阵,我们总能找到一个单位向量和标量,使得。
1.2.4 旋转的矩阵对数
如果代表一个旋转矩阵的指数坐标,那么反对称矩阵就是旋转矩阵的矩阵对数(matrix logarithm)。矩阵对数是矩阵指数的逆运算。矩阵指数是将角速度的矩阵表达积分1s得到一个旋转矩阵,矩阵对数是对旋转矩阵微分,得到一个恒定角速度的矩阵表达,如果对它积分1s,就会将矩阵旋转至。简单来说:
1.3 刚体运动和速度(Twist)
这一小节讨论刚体构型(configuration)和速度,与1.2节讨论的旋转和角速度在某些方面是类似的。齐次变换矩阵与旋转矩阵类似,螺旋轴