如何利用JAVA实现走迷宫程序

本Demo使用三个类

一个Test类

一个自定义的Stack类

一个自定义的Queue类

可以实现的功能：

1.对于一个写在文本文件中的迷宫，能够将其转换为二维数组用广度优先搜索实现查找最短路径

2.可以不定义迷宫的入口和出口，能自动查找到出入口

前提是要有一个对应路径的.txt文件

这里举个例子吧,我的是"F:/1号迷宫(0,18).txt"路径下

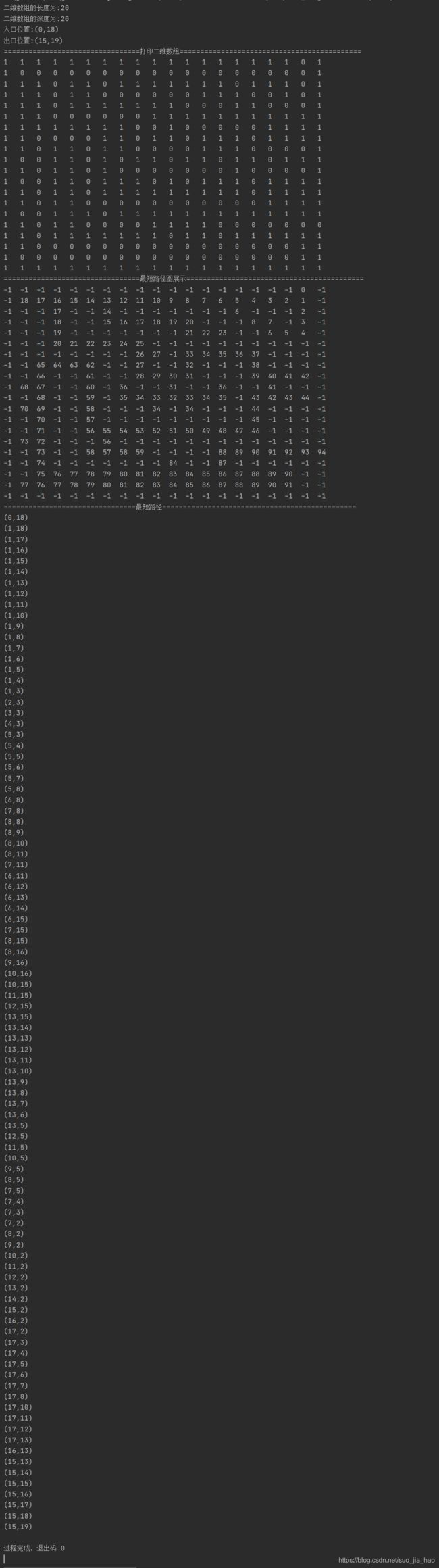
运行结果

示例代码

注释写的很详细，这里就不多赘述了

package com;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;

/**迷宫测试
 * 1号迷宫(0,18).txt
 *2号迷宫(0,1).txt
 */
public class Test {
    public static void main(String[] args) throws Exception {
        Test test = new Test();
        //通过文件输入流得到二维数组
        char[][] arr = test.getFile("F:/1号迷宫(0,18).txt");
        System.out.println("二维数组的长度为:"+arr[0].length);
        int deep = test.getDeepByChar(arr);
        System.out.println("二维数组的深度为:"+deep);

        //找到入口位置
        int [] begin = test.begin(arr);
        System.out.println("入口位置:("+begin[0]+","+begin[1]+")");
        //找到出口位置
        int [] end = test.end(arr,deep);
        System.out.println("出口位置:("+end[0]+","+end[1]+")");
        System.out.println("=================================打印二维数组============================================");
        //打印二维数组
        test.printArr(arr,deep);
        System.out.println("=================================最短路径图展示===========================================");
        //求最短路径图
        int[][] bfs = test.bfs(arr,begin,end,deep);
        for (int i = 0; i < deep; i++) {
            for (int j = 0; j < bfs[0].length; j++) {
                System.out.print(bfs[i][j]+"\t");
            }
            System.out.println();
        }
        System.out.println("================================最短路径===============================================");
        //根据最短路径图得到最短路径
        int[][] result = test.getLoaderFromMap(bfs, begin, end, deep);
        //得到result的深度
        int deep1 = test.getDeepByInt(result);
        for (int i = 0; i < deep1; i++) {
            System.out.println("("+result[i][0]+","+result[i][1]+")\t");
        }
    }

    //求最短路径图
    public int[][] bfs(char [][] arr, int [] begin, int [] end,int deep) {
        //移动的四个方向
        int[] dx = {1, 0, -1, 0};
        int[] dy = {0, 1, 0, -1};
        //d二维数组用来表示路径图
        int[][] d = new int [deep][arr[0].length];
        //储存未进行处理的节点,这里LinkedList实现了Deque,Deque又继承了Queue
        Queue1 que = new Queue1<>();
//        Queue que = new LinkedList<>();
        //将所有的位置都初始化为最大
        for(int i = 0; i < d.length; i++) {
            for(int j = 0; j < d[0].length; j++) {
                d[i][j] = -1;
            }
        }
        //将起始点放入队列
        que.offer(begin);
        //将起始点最短路径设为0
        d[begin[0]][begin[1]] = 0;
        //一直循环直到队列为空
        while(!que.isEmpty()) {
            //取出队列中最前端的点
            int [] current = que.poll();
            //如果是终点则结束
            if(current[0] == end[0] && current[1] == end[1]){
                break;
            }
            //四个方向循环
            for(int i = 0; i < 4; i++) {
                //试探
                int nx = current[0] + dx[i];
                int ny = current[1] + dy[i];
                //判断是否可以走
                if(nx >= 0 && nx < deep && ny >= 0 && ny < d[0].length  && arr[nx][ny] == '0' && d[nx][ny] == -1) {
                    //如果可以走，则将该点的距离加1
                    d[nx][ny] = d[current[0]][current[1]] + 1;
                    //并将该点放入队列等待下次处理
                    int[] c = {nx, ny};
                    que.offer(c);
                }
            }
        }
        return d;
    }

    //根据最短路径图得到最短路径
    private int [][] getLoaderFromMap(int [][] map,int [] begin,int [] end,int deep) {
        int k = 0;//标志位
        //创建二维数组最终正序存储结果
        int[][] resultList = new int[map.length * map.length][2];
        //result数组存储每个正确位置的下标
        int[] result;
        //创建一个栈,从出口开始把位置压入栈，之后再遍历栈就是正的迷宫顺序
        Stack1 stack = new Stack1<>();
        //先把出口压入栈
        stack.push(end);
        //移动的四个方向
        int[] dx = {1, 0, -1, 0};
        int[] dy = {0, 1, 0, -1};
        //已知出口和入口,从出口逆推入口
        //只要出口没有和入口下标重合，就一直循环
        while(true){
            //获得栈中最顶层元素，不取出
            int[] current = stack.peek();
            for (int i = 0; i < 4; i++) {
                //试探
                int nx = current[0] + dx[i];
                int ny = current[1] + dy[i];
                //如果当前节点不是入口节点，就继续向前追溯
                if(map[current[0]][current[1]] != map[begin[0]][begin[1]]){
                    //判断是否可以走
                    if (nx >= 0 && nx < deep && ny >= 0 && ny < map[0].length && map[nx][ny] != -1) {
                        //从后往前追溯，前一个数值一定比后一个小1
                        if(map[nx][ny] == map[current[0]][current[1]]-1){
                            //如果可以走,将此节点入栈
                            result = new int[]{nx, ny};
                            stack.push(result);
                        }
                    }
                }else{
                    k++;
                    break;
                }
            }
            //k是为了打破最外层循环，在比较map[current[0]][current[1]] != map[begin[0]][begin[1]]时
            //如果当前节点等于入口时，就应该打破循环，但是while和for是两重循环，所以加一个标志位再打破一次
            if(k != 0){
                break;
            }
        }

        //取出栈中元素赋给resultList
        int len = stack.length();
        for(int i = 0;i < len;i++){
            result = stack.pop();
            resultList[i][0] = result[0];
            resultList[i][1] = result[1];
        }
        return resultList;
    }

    //把文件中的二进制转换为二维数组
    private char[][] getFile (String pathName) throws Exception {
        File file = new File(pathName);
        //文件不存在时抛出异常
        if (!file.exists())
            throw new RuntimeException("Not File!");
        //字符缓冲输入流//缓冲流是处理流，要先new一个字符输入流
        BufferedReader br = new BufferedReader(new FileReader(file));
        //字符串str用来存储一行数据
        String str;
        //初始化一个二维数组
        char[][] arr = new char[110][];
        //x用来记录读取的行数
        int x = 0;
        while ((str = br.readLine()) != null) {
            x++;
            //把字符串变成字符数组存储
            char[] cArr = str.toCharArray();
            //把一行字符数组加入到二维数组中
            arr[x - 1] = cArr;
        }
        br.close();
        return arr;
    }

    //找到入口位置
    private int[] begin ( char[][] arr){
        //存储起点的下标begin[0]=x,begin[1]=y
        int[] begin = new int[2];
        //用StringBuffer把数组转为字符串，方便找到其中的元素
        StringBuffer s = new StringBuffer();
        for (int i = 0; i < arr[0].length; i++) {
            s.append(arr[0][i]);
        }
        //如果入口在第一行
        //判断下标是否存在
        if (s.indexOf("0") != -1) {
            begin[0] = 0;
            begin[1] = s.indexOf("0");
            return begin;
        } else {
            //如果入口在第一列
            for (int i = 0; i < arr.length; i++) {
                if (arr[i][0] == '0') {
                    begin[0] = i;
                    begin[1] = 0;
                    return begin;
                }
            }
        }
        return begin;
    }

    //找到出口位置
    private int[] end ( char[][] arr, int deep){
        //存储出口的下标end[0]=x,end[1]=y
        int[] end = new int[2];
        //出口在最后一列上     //18是第二个表的深度
        for (int i = 0; i < deep; i++) {
            //最后一列上找到出口
            if (arr[i][arr[0].length - 1] == '0') {
                end[0] = i;
                end[1] = arr[0].length - 1;
                return end;
            }
        }
        //出口在最后一行上
        for (int i = 0; i < arr.length; i++) {
            //最后一行上找到出口    //deep为最后一行的下标
            if (arr[deep - 1][i] == '0') {
                end[0] = deep - 1;
                end[1] = i;
                return end;
            }
        }
        return end;
    }

    /**
     * 由于二维数组刚创建时的默认行数为110，但是实际存储不到110，在对二维数组进行遍历得到实际有效深度时
     * 就会抛出数组下标越界异常，发生越界异常可认为到达二维数组的深度边缘，此时的深度就是有效深度
     * 将异常捕获，返回此时深度就可以得到二维数组的有效深度
     */
    //得到二维数组有效深度
    private int getDeepByChar ( char[][] arr){
        int y = 0;//深度
        for (int i = 0; i < arr.length; i++) {
            //由于i可能越界，当i越界时就认为到达最底部,返回当前y值
            try {
                //如果第一列那行数据不为1或0，就认为此行无效
                if (arr[i][0] != '1' && arr[i][0] != '0') {
                    break;
                }
            } catch (Exception e) {
                return y;
            }
            y++;
        }
        return y;
    }

    //得到二维整形数组有效深度
    private int getDeepByInt ( int[][] arr){
        int y = 0;//深度
        for (int i = 0; i < arr.length; i++) {
            //如果遇到(0,0)的，认为已经失效
            if (arr[i][0] == 0 && arr[i][1] == 0) {
                break;
            }
            y++;
        }
        return y;
    }

    //打印二维数组
    private void printArr ( char[][] arr, int deep){
        for (int i = 0; i < arr[0].length; i++) {
            for (int j = 0; j < deep; j++) {
                try {
                    System.out.print(arr[i][j] + "\t");
                } catch (Exception e) {
                }
            }
            System.out.println();
        }
    }
}

/**
 * 队列
 * @param 
 */
class Queue1 {
    private E[] arr;//使用数组表示一个队列
    private int size;//size表示队列中有效元素个数
    private int putIndex=-1;//putIndex表示从队列中放数的索引始终从队首取，并且取得索引始终为arr[0]

    //有参构造
    protected Queue1(int initSize){
        if(initSize < 0){
            throw new IllegalArgumentException("参数错误");
        }
        arr = (E[])new Object[initSize];
        size = 0;
    }
    //无参构造，默认10个长度大小
    protected Queue1(){
        this(110);
    }

    //入队
    protected void offer(E e){
        if(size == arr.length) {
            throw new ArrayIndexOutOfBoundsException("无法进行push操作，队列已满");
        }
        arr[++putIndex] = e;
        size++;
    }

    //判断队列是否为空
    protected boolean isEmpty(){
        return size == 0?true:false;
    }

    //出队
    protected E poll() {
        if (size == 0) {
            throw new ArrayIndexOutOfBoundsException("This queue is empty!当前队列为空");
        }
        E tmp = arr[0];
        //后面的元素向前移动
        for (int i = 0; i < size - 1; i++) {
            arr[i] = arr[i + 1];
        }
        arr[size - 1] = null;
        putIndex--;
        size--;
        return tmp;
    }
}

/**
 * 栈
 * @param 
 */
class Stack1 {
    private int maxSize;//最大长度
    private int top = -1;//栈顶指针，初始指向-1
    private E[] data;//数组代替栈存放元素

    //初始化栈大小
    protected Stack1(int maxSize){
        if(maxSize > 0){
            this.maxSize = maxSize;
            //data数组对象也要初始化大小
            data = (E[])new Object[maxSize];
        }else{
            throw new IllegalArgumentException("初始化栈大小失败，参数不合法");
        }
    }

    //默认初始化大小为10
    protected Stack1(){
        //调用有参构造，传入10
        this(10);
    }

    //入栈
    protected boolean push(E e){
        //先判断栈是否已满
        if(top == maxSize-1){
            //扩容
            this.resize();
        }
        //先top++,再top = e
        data [++top] = e;
        return true;
    }

    //判断栈是否为空
    protected boolean isEmpty(){
        return top == -1;
    }

    //得到栈的长度
    protected int length(){
        return top+1;
    }
    //出栈
    protected E pop(){
        //先判断栈是否为空
        if(top == -1){
            throw new IllegalArgumentException("栈当前为空");
        }
        else{
            E e = data[top];
            //先top = null,再top--
            data[top--] = null;
            return  e;
        }
    }

    //查看栈顶元素
    protected E peek(){
        //先判断栈是否为空
        if(top == -1){
            throw new IllegalArgumentException("栈当前为空");
        }else{
            return data[top];
        }
    }

    //栈扩容，默认扩容为原来的一倍
    protected void resize(){
        int newSize = maxSize*2;
        E[] newData = (E[])new Object[newSize];
        for (int i = 0;i < data.length;i ++){
            newData[i] = data[i];
        }
        //刷新最大长度
        maxSize = newSize;
        //再把newData赋值给data数组
        data = newData;
    }
}

总结

到此这篇关于如何利用JAVA实现走迷宫程序的文章就介绍到这了,更多相关JAVA走迷宫程序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！