?p=23646

你可能会问，为什么是copulas？我们指的是数学上的概念。简单地说，copulas是具有均匀边际的联合分布函数。最重要的是，它们允许你将依赖关系与边际分开研究。有时你对边际的信息比对数据集的联合函数的信息更多，而copulas允许你建立关于依赖关系的 "假设 "情景。copulas可以通过将一个联合分布拟合到均匀分布的边际上而得到，这个边际是通过对你感兴趣的变量的cdf进行量化转换而得到的。

这篇文章是关于Python的（有numpy、scipy、scikit-learn、StatsModels和其他你能在Anaconda找到的好东西），但是R对于统计学来说是非常棒的。我重复一遍，R对统计学来说是非常棒的。如果你是认真从事统计工作的，不管你是否喜欢R，你至少应该看看它，看看有哪些包可以帮助你。很有可能，有人已经建立了你所需要的东西。而且你可以从python中使用R（需要一些设置）。

说了这么多关于R的好处，我们还是要发一篇关于如何在python中使用一个特定的数学工具的文章。因为虽然R很牛，但python确实有令人难以置信的灵活性，可以用来处理其他事务。

这篇文章中即将出现的大部分内容都会用Jupyter Notebooks来构建。

软件

我很惊讶，scikit-learn或scipy中没有明确的copula包的实现。

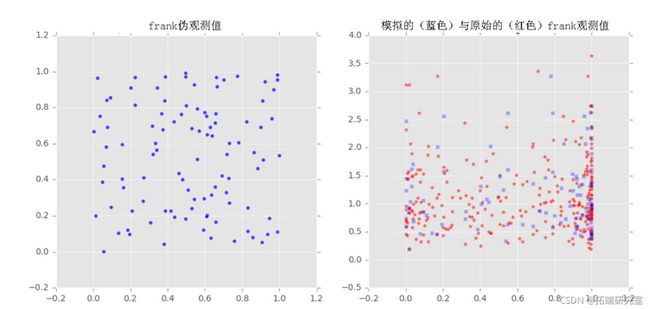
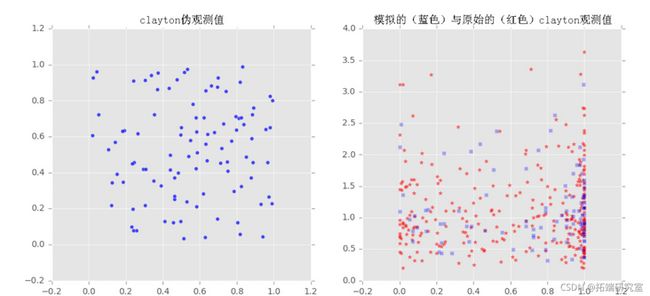
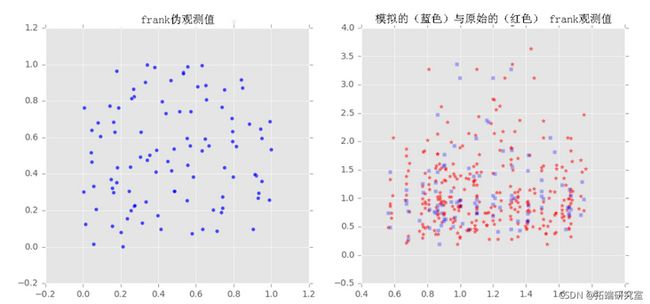
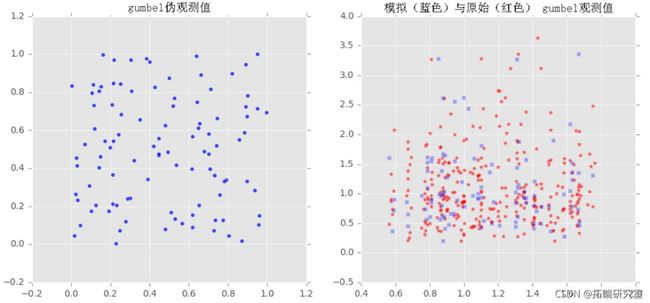
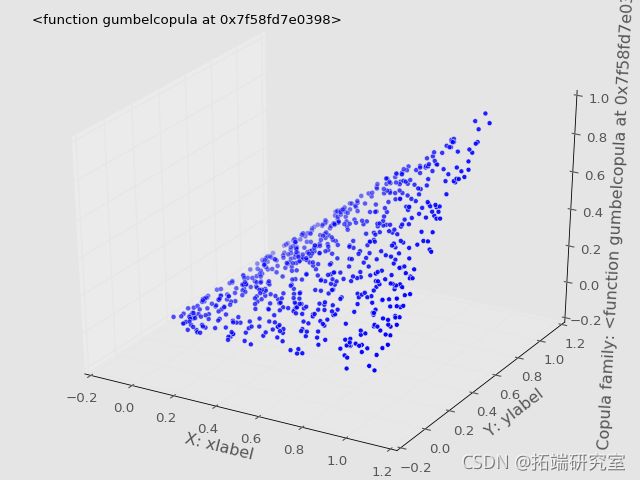
2D数据的Frank、Clayton和Gumbel copula

测试

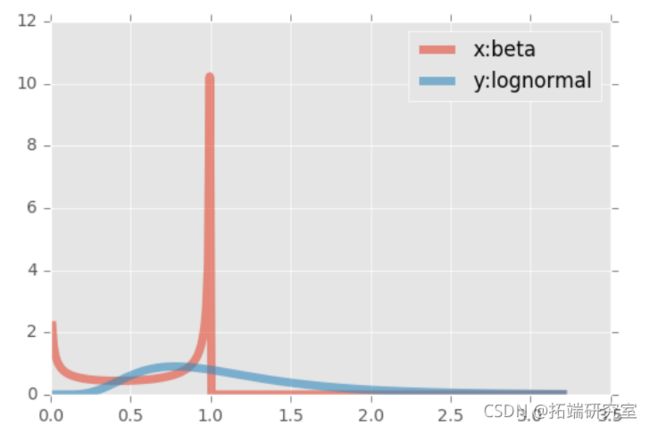
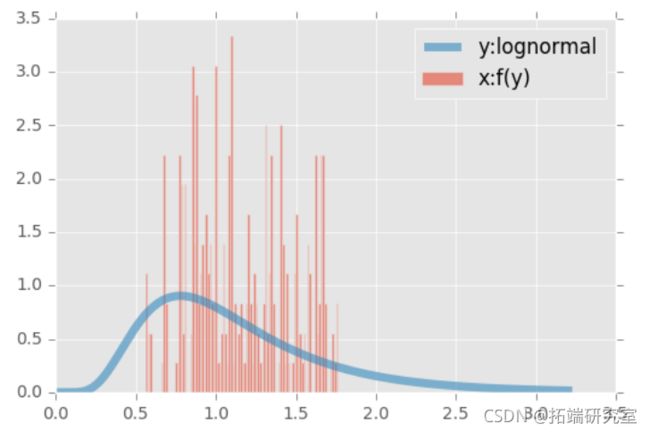
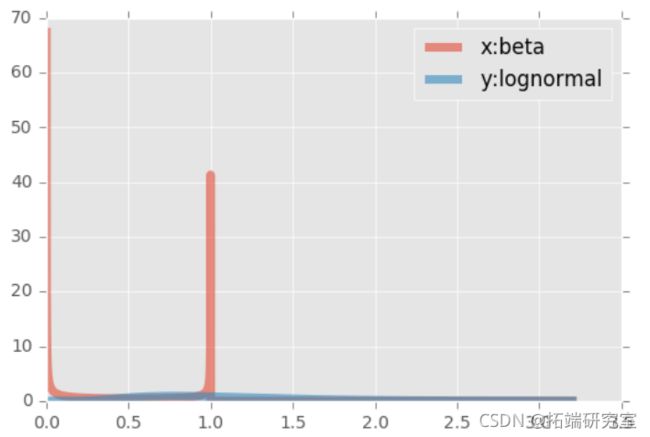
第一个样本（x）是从一个β分布中产生的，（y）是从一个对数正态中产生的。β分布的支持度是有限的，而对数正态的右侧支持度是无穷大的。对数的一个有趣的属性。两个边际都被转换到了单位范围。

我们对样本x和y拟合了三个族（Frank, Clayton, Gumbel）的copulas，然后从拟合的copulas中提取了一些样本，并将采样输出与原始样本绘制在一起，以观察它们之间的比较。

    #等同于ppf，但直接从数据中构建 
    sortedvar=np.sort(var)    

    #绘制

    for index,family in enumerate(\['Frank', 'clayton', 'gumbel'\]):

            #获得伪观测值
            u,v = copula\_f.generate\_uv(howmany)

        #画出伪观测值
        axs\[index\]\[0\].scatter(u,v,marker='o',alpha=0.7)

      

    plt.show()

#总样本与伪观测值的对比
sz=300
loc=0.0 #对大多数分布来说是需要的
sc=0.5
y=lognorm.rvs(sc,loc=loc, size=sz)

独立（不相关）数据

我们将从β分布中抽取（x）的样本，从对数正态中抽取（y）的样本。这些样本是伪独立的（我们知道，如果你用计算机来抽取样本，就不会有真正的独立，但好在是合理的独立）。

#不相关的数据：一个β值（x）和一个对数正态（y）。
a= 0.45#2. #alpha
b=0.25#5. #beta

#画出不相关的x和y 
plt.plot(t, beta.pdf(t,a,b), lw=5, alpha=0.6, label='x:beta')


#绘制由不相关的x和y建立的共线性图
title='来自不相关数据的共线性 x: beta, alpha {} beta {}, y: lognormal, mu {}, sigma dPlot(title,x,y,pseudoobs)

相依性（相关）数据

自变量将是一个对数正态（y），变量（x）取决于（y），关系如下。初始值为1（独立）。然后，对于每一个点i, 如果 , 那么 , 其中c是从1的分数列表中统一选择的，否则, .

#相关数据：一个对数正态（y）。

#画出相关数据

 np.linspace(0, lognorm.ppf(0.99, sc), sz)
plt.plot(t, gkxx.pdf(t), lw=5, alpha=0.6,

拟合copula参数

没有内置的方法来计算archimedean copulas的参数，也没有椭圆elliptic copulas的方法。但是可以自己实现。选择将一些参数拟合到一个scipy分布上，然后在一些样本上使用该函数的CDF方法，或者用一个经验CDF工作。这两种方法在笔记本中都有实现。

因此，你必须自己写代码来为archimedean获取参数，将变量转化为统一的边际分布，并对copula进行实际操作。它是相当灵活的。

#用于拟合copula参数的方法 

# === Frank参数拟合
    """
    对这个函数的优化将给出参数 
    """
   #一阶debye函数的积分值    int_debye = lambda t: t/(npexp(t)-1.) 
    debye = lambda alphaquad(int_debye , 
                               alpha
                              )\[0\]/alpha
    diff = (1.-kTau)/4.0-(debye(-alpha)-1.)/alpha



#================
#clayton 参数方法
def Clayton(kTau):
    try:
        return 2.*kTau/(1.-kTau)
 

#Gumbel参数方法
def Gumbel(kTau):
    try:
        return 1./(1.-kTau)


#================
#copula生成

    #得到协方差矩阵P
    #x1=norm.ppf(x,loc=0,scale=1)
    #y1=norm.ppf(y,loc=0,scale=1)
    #return norm.cdf((x1,y1),loc=0,scale=P)




#================
#copula绘图

    fig = pylab.figure()
    ax = Axes3D(fig)

        ax.text2D(0.05, 0.95, label, transform=ax.transAxes)
        ax.set_xlabel('X: {}'.format(xlabel))
        ax.set_ylabel('Y: {}'.format(ylabel))


    #sample是一个来自U,V的索引列表。这样，我们就不会绘制整个copula曲线。
    if plot:
  
        print "绘制copula {}的样本".format(copulaName)
        returnable\[copulaName\]=copulapoints
        if plot:
            zeFigure=plot3d(U\[样本\],V\[样本\],copulapoints\[样本\], label=copulaName,

生成一些输入数据

在这个例子中，我们使用的是与之前相同的分布，探索copula 。如果你想把这段代码改编成你自己的真实数据，。

t = np.linspace(0, lognorm.ppf(0.99, sc), sz)

#从一些df中抽取一些样本
X=beta.rvs(a,b,size=sz)
Y=lognorm.rvs(sc,size=sz)
#通过对样本中的数值应用CDF来实现边缘分布
U=beta.cdf(X,a,b)
V=lognorm.cdf(Y,sc)

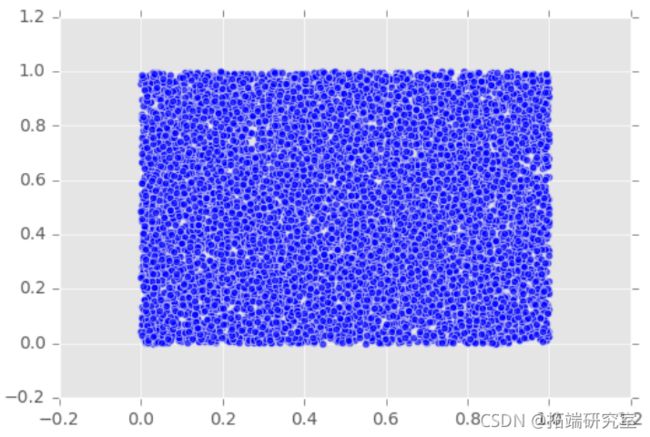
#画出它们直观地检查独立性
plt.scatter(U,V,marker='o',alpha=0.7)
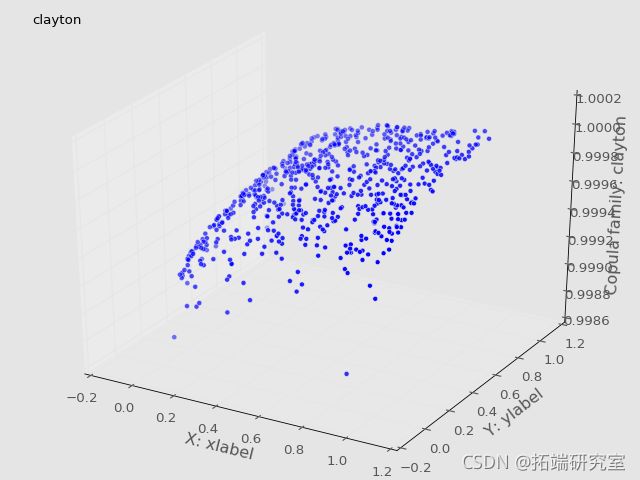
plt.show()

可视化Copulas

没有直接的构造函数用于高斯或t_Copulas_，可以为椭圆_Copulas_(_Elliptic_ _Copulas_)建立一个更通用的函数。

Samples=700
#选择用于抽样的copula指数
np.random.choice(range(len(U)),Samples)


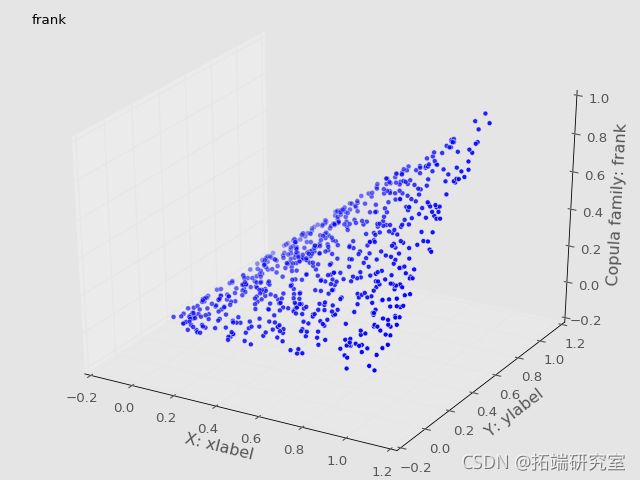
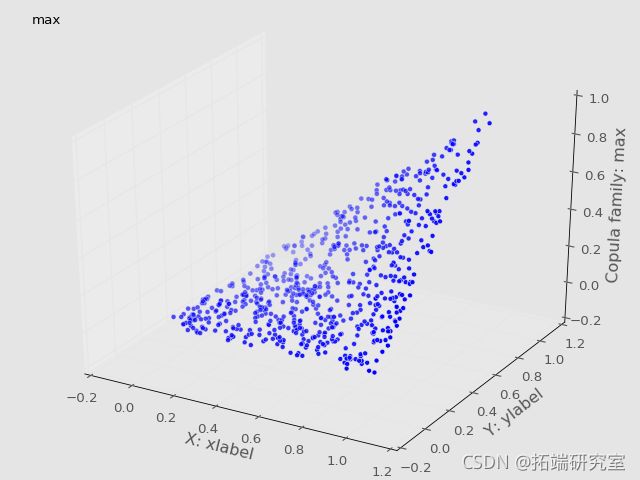
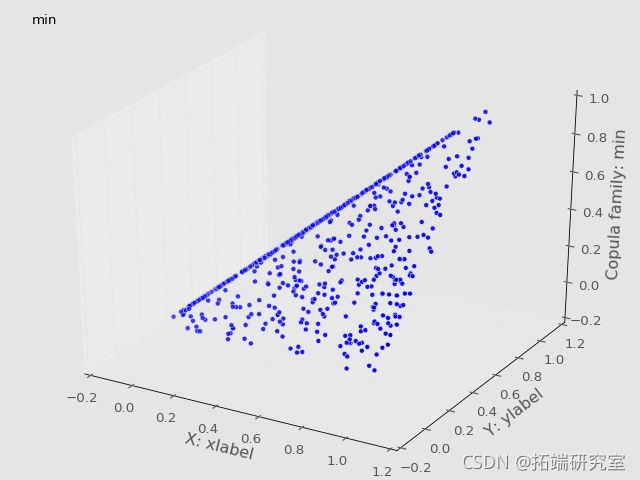
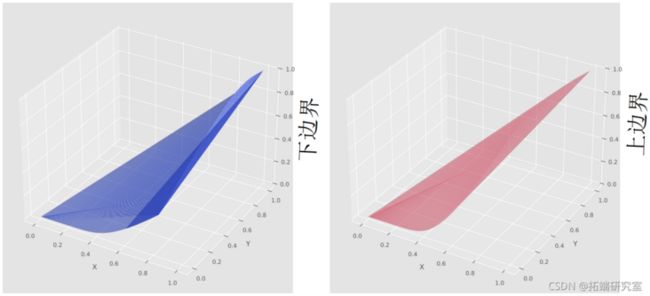
Plot(U,V)

Frechét-Höffding边界可视化

根据定理，我们将copula画在一起，得到了Frechét-Höffding边界。

#建立边界为copula的区域
plot_trisurf(U\[样本\],V\[样本\],copula\['min'\]\[样本\],
          c='red') #上限
plot_trisurf(U\[样本\],V\[样本\],copula\['max'\]\[样本\],
           c='green') #下限