R语言 生存分析与cox模型的学习笔记

---

前言

http://www.sthda.com/ 是个好网站，Clinical Statistics: Introducing Clinical Trials, Survival Analysis, and Longitudinal Data Analysis 是本好书。

---

提示：

一、基础概念

Survival time and event（生存时间或事件）
常见的event：Relapse（复发），Progression，Death。
Censoring （删失）生存分析主要产生censoring或者drop out的原因是回访时间点，event没有发生，这种情况被称为right-censored，这种情况会导致censored survival times（截尾时间）偏短，我们可能会得到一个低估的数据。
Survival function and hazard function （生存函数和风险函数）用来衡量survial的表现形式和预测手段。

1、解读 Survival function

The survival function 生存函数

$$S(t)$$
通俗的解释，就是某病人活到时间点 t 的概率。假如病人在大写T的时间点，没有出现Event。此病人活过t时间点的概率。假定 F(t) 是病人没有活过时间点的概率，那么
$$S(t)=1-F(t)=P(T>t)$$
生存函数，换言之，就等于时间点大写T（大T应该大于等于0的随机变量）大于某个时间点小写t。
生存函数是一个分布函数，我们求一个概率密度函数。
$$S(t)=P(T>t)={\int }_t^{\infty }f(x)dx=1-F(t)$$

2、解读 Hazard function

The hazard function 风险函数
$$h(t)$$
这是一个描述“瞬间死亡率”的函数，具体指观察对象，在生存到t 时刻的瞬时死亡率。区别于S (t) 生存函数表示超过某时间点t1 概率，风险函数描述在时间点t2 ，观察对象的死亡率。
那么，这个瞬间是什么，就是
$$T<t+dt|T>t$$
这表示，病人在 T > t 的基础上，也就是在时间t，EVENT没有发生。下一个瞬间t+dt马上就发生。
那么这个概率，就等于
$$P（T<t+dt|T>t）=\frac{P（t<T<t+dt)}{P(T>t)}=\frac{f（t）dt}{S（t）}=h(t)dt$$

把最后两项的dt出掉，就得到了我们熟悉的。
$$\frac{f（t）}{S（t）}=h(t)$$
h(t) 既不是概率密度，也不是累积分布。

3、解读 Kaplan-Meier survival estimate

KM方法是用来估计S (t)的，因为各种各样的原因，实际情况很难准确计算S (t)。
$$S(t)=\prod _{i:t_i<=t}(1-\frac{d_i}{n_i})$$
ti 是样本中，每个数据的记录时间，可以肯定的事ti 是离散的，S(t)也必然是离散的。
di 是在ti这个时间点，死亡（event 发生）的人数。
ni 在这个时间点，取出删失后的生存人数。也就是减去删失的，上一个时间点死亡的人数。
可以预见的，在ti 与 ti+1 这个时间段中的t，S (t) 是一个固定值，因为ti是一个离散的数据，所以KM曲线会表现为台阶形。

二、用R来实现

这部分，参考http://www.sthda.com/english/wiki/survival-analysis-basics。

1、K-M 曲线可视化

生存分析的R包，用survial，survminer就可以了

#install.packages(c("survival", "survminer"))
library("survival")
library("survminer")、
data <- lung
# data("lung") 已经不适合这个版本了

包里自带的lung数据集
inst: Institution code
time: Survival time in days
status: censoring status 1=censored, 2=dead
age: Age in years
sex: Male=1 Female=2
ph.ecog: ECOG performance score (0=good 5=dead)
ph.karno: Karnofsky performance score (bad=0-good=100) rated by physician
pat.karno: Karnofsky performance score as rated by patient
meal.cal: Calories consumed at meals
wt.loss: Weight loss in last six months

> head(lung)
  inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1    3  306      2  74   1       1       90       100     1175      NA
2    3  455      2  68   1       0       90        90     1225      15
3    3 1010      1  56   1       0       90        90       NA      15
4    5  210      2  57   1       1       90        60     1150      11
5    1  883      2  60   1       0      100        90       NA       0
6   12 1022      1  74   1       1       50        80      513       0

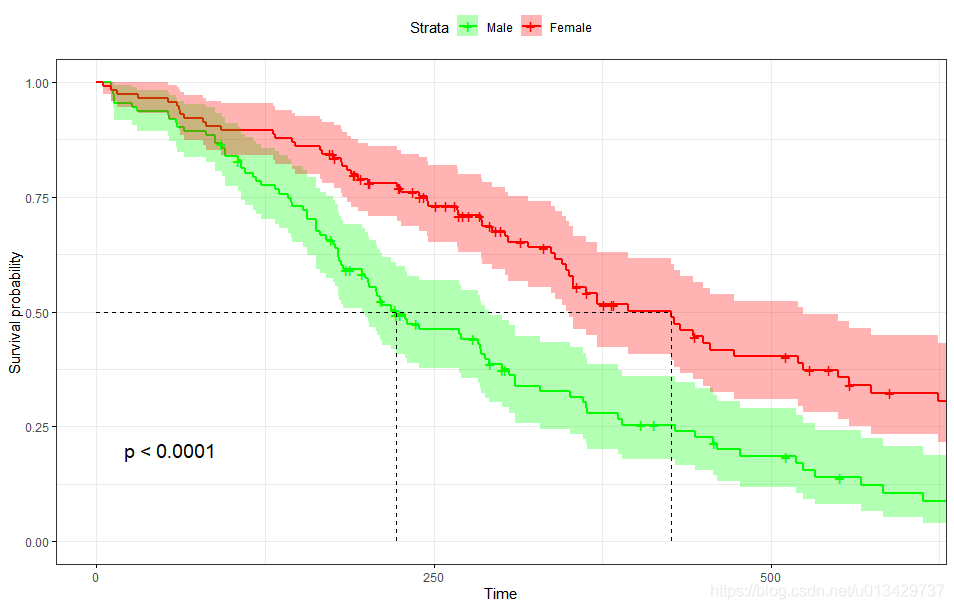
> fit <- survfit(Surv(time, status) ~ sex, data = lung)
> print(fit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)

        n events median 0.95LCL 0.95UCL
sex=1 138    112    270     212     310
sex=2  90     53    426     348     550

通过SEX把sample分成两组。

> summary(fit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)

                sex=1 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
   11    138       3   0.9783  0.0124       0.9542        1.000
   12    135       1   0.9710  0.0143       0.9434        0.999
   13    134       2   0.9565  0.0174       0.9231        0.991
   15    132       1   0.9493  0.0187       0.9134        0.987
   26    131       1   0.9420  0.0199       0.9038        0.982
   30    130       1   0.9348  0.0210       0.8945        0.977
   31    129       1   0.9275  0.0221       0.8853        0.972
   53    128       2   0.9130  0.0240       0.8672        0.961

$$S(t)=\prod _{i:t_i<=t}(1-\frac{d_i}{n_i})$$
对应公示，ti 是time，ni 是n.risk, di 是n.event。
其余的colname如下：
n: total number of subjects in each curve.
time: the time points on the curve.
n.risk: the number of subjects at risk at time t
n.event: the number of events that occurred at time t.
n.censor: the number of censored subjects, who exit the risk set, without an event, at time t.
lower,upper: lower and upper confidence limits for the curve, respectively.
strata: indicates stratification of curve estimation. If strata is not NULL, there are multiple curves in the result. The levels of strata (a factor) are the labels for the curves.

# 把summary中统计学数据看得通透
> summary(fit)$table
      records n.max n.start events   *rmean *se(rmean) median 0.95LCL
sex=1     138   138     138    112 326.0841   22.91156    270     212
sex=2      90    90      90     53 460.6473   34.68985    426     348
  0.95UCL
sex=1     310
sex=2     550

# 可视化
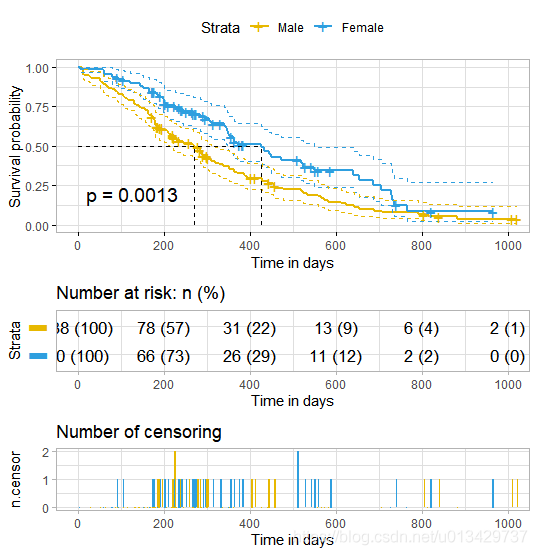
ggsurvplot(fit,
           pval = TRUE, conf.int = TRUE,
           risk.table = TRUE, # Add risk table
           risk.table.col = "strata", # Change risk table color by groups
           linetype = "strata", # Change line type by groups
           surv.median.line = "hv", # Specify median survival
           ggtheme = theme_bw(), # Change ggplot2 theme
           palette = c("#E7B800", "#2E9FDF"))

linetype = “strata”, # Change line type by groups 这一行负责实线和虚线，强迫症必改。
按照教程例子，加一点细节。

ggsurvplot(
  fit,                     # survfit object with calculated statistics.
  pval = TRUE,             # show p-value of log-rank test.
  conf.int = TRUE,         # show confidence intervals for 
  # point estimaes of survival curves.
  conf.int.style = "step",  # customize style of confidence intervals
  xlab = "Time in days",   # customize X axis label.
  break.time.by = 200,     # break X axis in time intervals by 200.
  ggtheme = theme_light(), # customize plot and risk table with a theme.
  risk.table = "abs_pct",  # absolute number and percentage at risk.
  risk.table.y.text.col = T,# colour risk table text annotations.
  risk.table.y.text = FALSE,# show bars instead of names in text annotations
  # in legend of risk table.
  ncensor.plot = TRUE,      # plot the number of censored subjects at time t
  surv.median.line = "hv",  # add the median survival pointer.
  legend.labs = 
    c("Male", "Female"),    # change legend labels.
  palette = 
    c("#E7B800", "#2E9FDF") # custom color palettes.
)

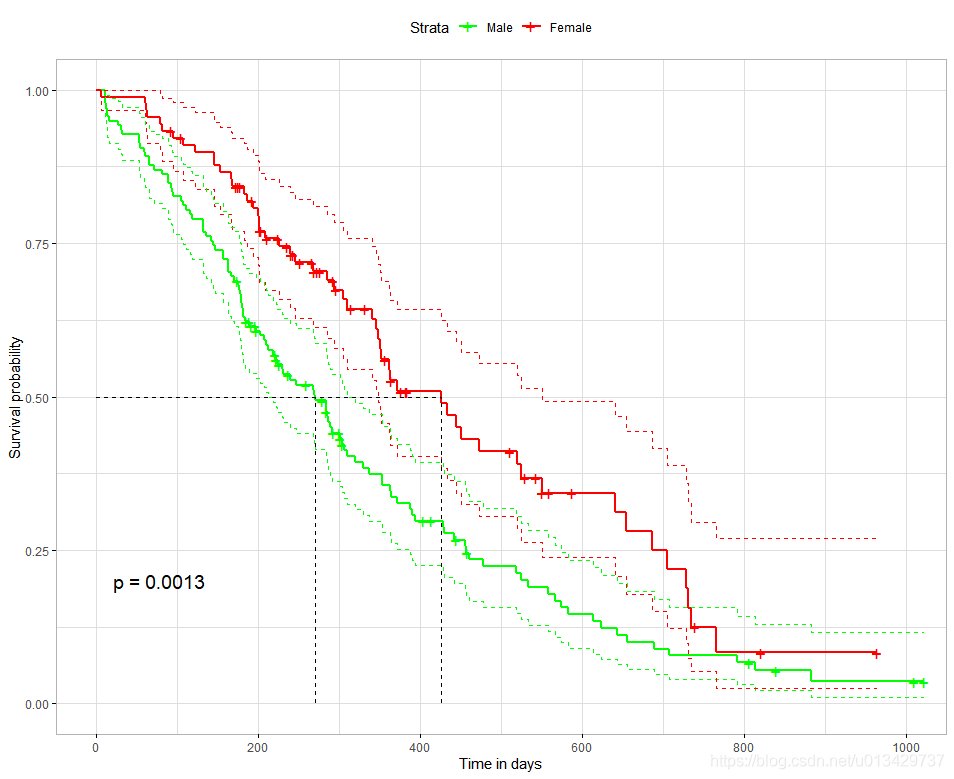
#一般不用这么复杂的
ggsurvplot(
  fit,                     # survfit object with calculated statistics.
  pval = TRUE,             # show p-value of log-rank test.
  conf.int = TRUE,         # show confidence intervals for 
  # point estimaes of survival curves.
  conf.int.style = "step",  # customize style of confidence intervals
  xlab = "Time in days",   # customize X axis label.
  break.time.by = 200,     # break X axis in time intervals by 200.
  ggtheme = theme_light(), # customize plot and risk table with a theme.
  #risk.table = "abs_pct",  # absolute number and percentage at risk.
  #risk.table.y.text.col = T,# colour risk table text annotations.
  #risk.table.y.text = FALSE,# show bars instead of names in text annotations
  # in legend of risk table.
  #ncensor.plot = TRUE,      # plot the number of censored subjects at time t
  surv.median.line = "hv",  # add the median survival pointer.
  legend.labs = 
    c("Male", "Female"),    # change legend labels.
  palette = 
    c("green", "red"), # custom color palettes.
)

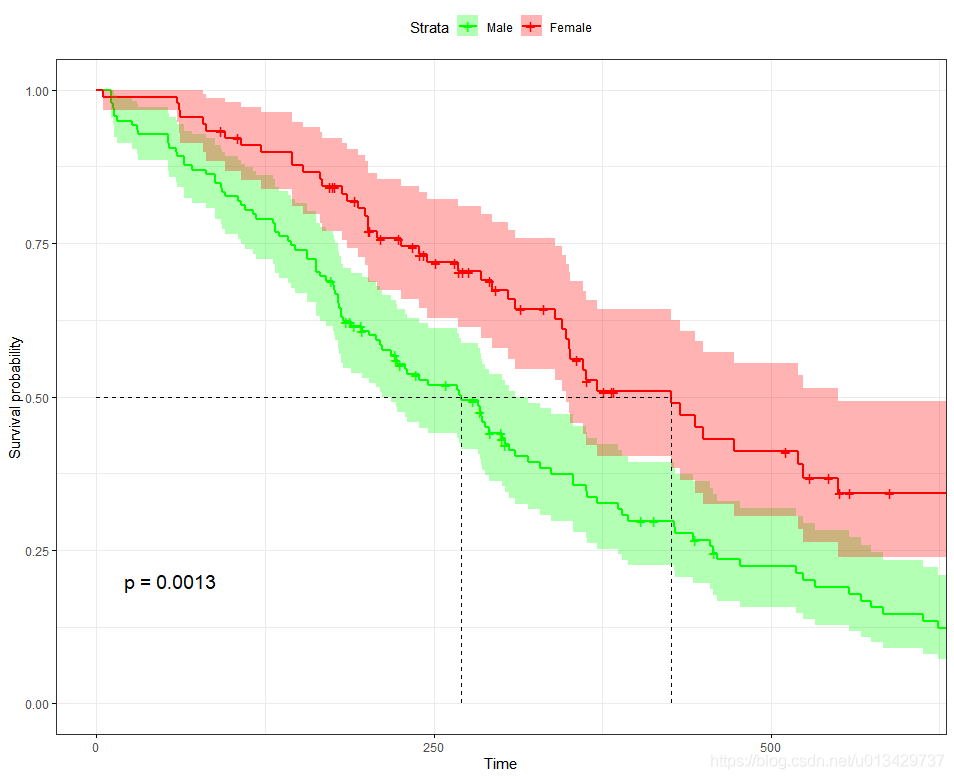
#xlim调整横坐标
ggsurvplot(fit,
           conf.int = TRUE,
           risk.table.col = "strata", # Change risk table color by groups
           ggtheme = theme_bw(), # Change ggplot2 theme
           palette = c("green", "red"),
           xlim = c(0, 600),
           surv.median.line = "hv",  # add the median survival pointer.
           legend.labs = 
             c("Male", "Female"),    # change legend labels.
           pval = TRUE
           )

2、Log-Rank 检验

survdiff() 比较两条生存曲线的差异。

> surv_diff <- survdiff(Surv(time, status) ~ sex, data = lung)
> surv_diff
Call:
survdiff(formula = Surv(time, status) ~ sex, data = lung)

        N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 138      112     91.6      4.55      10.3
sex=2  90       53     73.4      5.68      10.3

 Chisq= 10.3  on 1 degrees of freedom, p= 0.001

n: the number of subjects in each group.
obs: the weighted observed number of events in each group.
exp: the weighted expected number of events in each group.
chisq: the chisquare statistic for a test of equality.
strata: optionally, the number of subjects contained in each stratum.

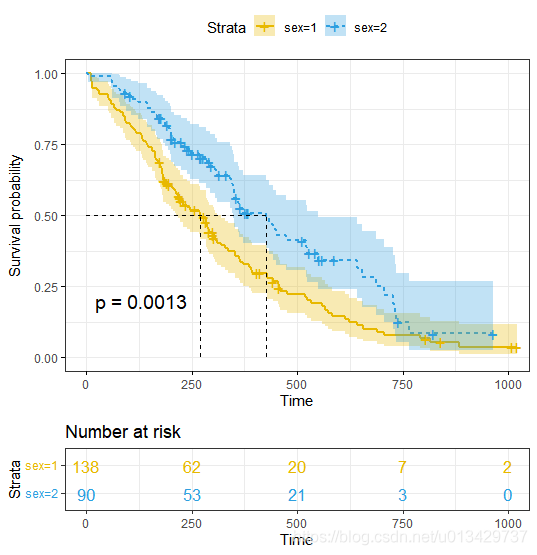
最值得关注就是p-value了， p = 0.0013, 两组生存曲线具有显著性差异。

三、The Cox proportional hazards model （PH 模型）

1、Cox proportional hazards model 基础概念

proportional hazards model是对h（t）的建模
$$h(t,x_1,x_2,...,x_p)=h_0(t)\times exp(b_1{x}_1+b_2{x}_2+...+b_p{x}_p)$$
其中h0(t)被叫做baseline hazard function，基线。 后面作为指数的b1，b2，b3, b4…bp系数是我们需要计算的。每个人的x1，x2，x3…xn是每个数据样本的特征。把病人A的h（ta）除以病人B的h（tb），得到
$$\frac{h（t_a）}{h（t_b）}=\frac{exp（b_1{x}_{a1}+b_2{x}_{a2}+...+b_p{x}_{ap}）}{exp（b_1{x}_{b1}+b_2{x}_{b2}+...+b_p{x}_{bp}）}$$
$$\frac{exp（b_1{x}_{a1}+b_2{x}_{a2}+...+b_p{x}_{ap}）}{exp（b_1{x}_{b1}+b_2{x}_{b2}+...+b_p{x}_{bp}）}=exp（b_1（x_{a1}-x_{b1}）+b_2（x_{a2}-x_{b2}）+...+b_p（x_{ap}-x_{bp}))$$
可以发现，h0(t)被神奇的约掉了。
结论是：
HR = 1: No effect
HR < 1: Reduction in the hazard
HR > 1: Increase in Hazard

2、R 代码实现

library("survival")
library("survminer")
#data("lung")
lung <- lung
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
res.cox
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)

       coef exp(coef) se(coef)      z       p
sex -0.5310    0.5880   0.1672 -3.176 0.00149

Likelihood ratio test=10.63  on 1 df, p=0.001111
n= 228, number of events= 165 
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
  n= 228, number of events= 165 
       coef exp(coef) se(coef)      z Pr(>|z|)   
sex -0.5310    0.5880   0.1672 -3.176  0.00149 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
    exp(coef) exp(-coef) lower .95 upper .95
sex     0.588      1.701    0.4237     0.816
Concordance= 0.579  (se = 0.022 )
Rsquare= 0.046   (max possible= 0.999 )
Likelihood ratio test= 10.63  on 1 df,   p=0.001111
Wald test            = 10.09  on 1 df,   p=0.001491
Score (logrank) test = 10.33  on 1 df,   p=0.00131

The Cox regression results can be interpreted as follow:

Statistical significance. The column marked “z” gives the Wald statistic value. It corresponds to the ratio of each regression coefficient to its standard error (z = coef/se(coef)). The wald statistic evaluates, whether the beta (β) coefficient of a given variable is statistically significantly different from 0. From the output above, we can conclude that the variable sex have highly statistically significant coefficients.

The regression coefficients. The second feature to note in the Cox model results is the the sign of the regression coefficients (coef). A positive sign means that the hazard (risk of death) is higher, and thus the prognosis worse, for subjects with higher values of that variable. The variable sex is encoded as a numeric vector. 1: male, 2: female. The R summary for the Cox model gives the hazard ratio (HR) for the second group relative to the first group, that is, female versus male. The beta coefficient for sex = -0.53 indicates that females have lower risk of death (lower survival rates) than males, in these data.

Hazard ratios. The exponentiated coefficients (exp(coef) = exp(-0.53) = 0.59), also known as hazard ratios, give the effect size of covariates. For example, being female (sex=2) reduces the hazard by a factor of 0.59, or 41%. Being female is associated with good prognostic.

Confidence intervals of the hazard ratios. The summary output also gives upper and lower 95% confidence intervals for the hazard ratio (exp(coef)), lower 95% bound = 0.4237, upper 95% bound = 0.816.

Global statistical significance of the model. Finally, the output gives p-values for three alternative tests for overall significance of the model: The likelihood-ratio test, Wald test, and score logrank statistics. These three methods are asymptotically equivalent. For large enough N, they will give similar results. For small N, they may differ somewhat. The Likelihood ratio test has better behavior for small sample sizes, so it is generally preferred.

用for循环把这几个nivariate coxph function都输出出来

library(tableone)
out=data.frame()
for (i in 4:length(lung)) {
     
  res.cox <- coxph(Surv(time, status) ~ lung[,i], data = lung)
  m=data.frame(ShowRegTable(res.cox))
  colnames(m)[1]="95%CI"
  coxsummary=summary(res.cox) 
  out=rbind (out,cbind(factor=colnames(lung)[i],
                       HR=coxsummary$coefficients[,"exp(coef)"],
                       wald.test=coxsummary$coefficients[,"z"],
                       CI =m[1],
                       pvalue=coxsummary$coefficients[,"Pr(>|z|)"])
             )
  }

> head(out)
                factor        HR  wald.test             95%CI       pvalue
lung[, i]        age 1.0188965  2.0349776 1.02 [1.00, 1.04] 4.185313e-02
lung[, i]1       sex 0.5880028 -3.1763850 0.59 [0.42, 0.82] 1.491229e-03
lung[, i]2   ph.ecog 1.6095320  4.1980499 1.61 [1.29, 2.01] 2.692234e-05
lung[, i]3  ph.karno 0.9836863 -2.8097590 0.98 [0.97, 1.00] 4.957861e-03
lung[, i]4 pat.karno 0.9803456 -3.6309353 0.98 [0.97, 0.99] 2.823960e-04
lung[, i]5  meal.cal 0.9998762 -0.5345802 1.00 [1.00, 1.00] 5.929402e-01

From the output above,

The variables sex, age and ph.ecog have highly statistically significant coefficients, while the coefficient for ph.karno is not significant.

age and ph.ecog have positive beta coefficients, while sex has a negative coefficient. Thus, older age and higher ph.ecog are associated with poorer survival, whereas being female (sex=2) is associated with better survival.

Now, we want to describe how the factors jointly impact on survival. To answer to this question, we’ll perform a multivariate Cox regression analysis. As the variable ph.karno is not significant in the univariate Cox analysis, we’ll skip it in the multivariate analysis. We’ll include the 3 factors (sex, age and ph.ecog) into the multivariate model.

#多因素的COX
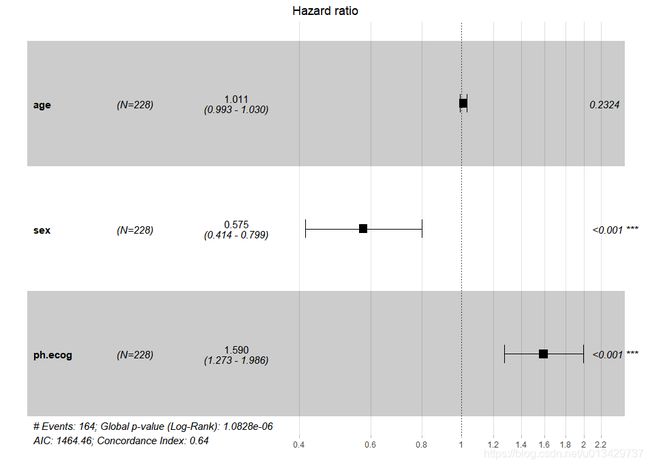
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data =  lung)
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)

  n= 227, number of events= 164 
   (1 observation deleted due to missingness)

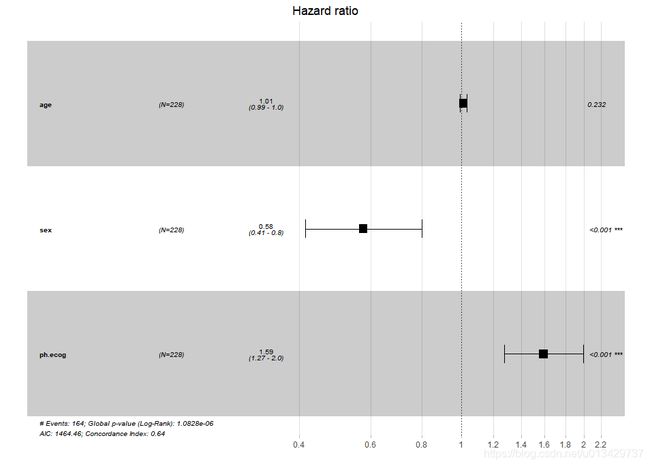
             coef exp(coef)  se(coef)      z Pr(>|z|)    
age      0.011067  1.011128  0.009267  1.194 0.232416    
sex     -0.552612  0.575445  0.167739 -3.294 0.000986 ***
ph.ecog  0.463728  1.589991  0.113577  4.083 4.45e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

        exp(coef) exp(-coef) lower .95 upper .95
age        1.0111     0.9890    0.9929    1.0297
sex        0.5754     1.7378    0.4142    0.7994
ph.ecog    1.5900     0.6289    1.2727    1.9864

Concordance= 0.637  (se = 0.025 )
Likelihood ratio test= 30.5  on 3 df,   p=1e-06
Wald test            = 29.93  on 3 df,   p=1e-06
Score (logrank) test = 30.5  on 3 df,   p=1e-06

#基础森林图
ggforest(res.cox, data = lung)

#加一点细节
ggforest(res.cox,  #coxph得到的Cox回归结果
         data = lung,  #数据集
         main = 'Hazard ratio',  #标题
         cpositions = c(0.01, 0.15, 0.35),  #前三列距离,从前往后看
         fontsize = 1, #字体大小
         refLabel = 'reference', #相对变量的数值标签，也可改为1
         noDigits = 3 #保留HR值以及95%CI的小数位数
         )

如果需要，还可以用step()做逐步回归。

#这个已经是最佳状态了
> AICsteps=step(res.cox,direction = "forward")
Start:  AIC=1464.46
Surv(time, status) ~ age + sex + ph.ecog

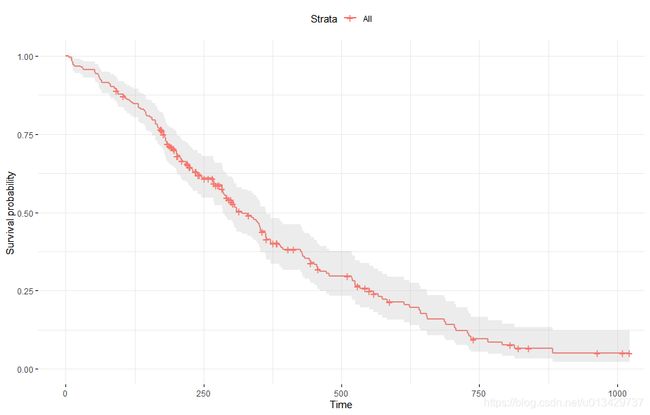
# KM 曲线可视化
fit <- survfit(res.cox, data = lung)
ggsurvplot(fit, conf.int = TRUE,
           ggtheme = theme_minimal())

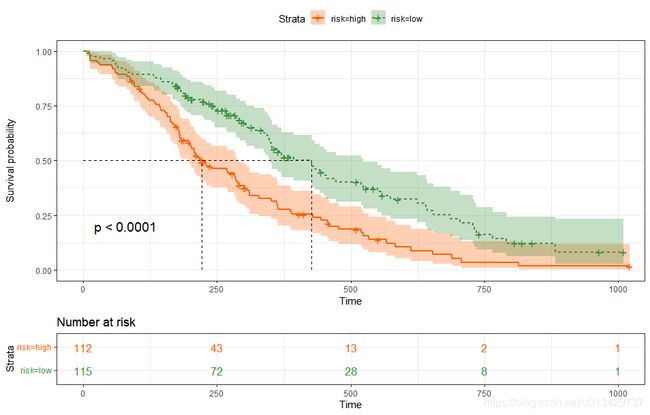
# 以median中位数做cut-off值，做个分组，比较KM曲线。
riskscore=predict(res.cox,type="risk",newdata = lung)
risk=as.vector(ifelse(riskscore > median(na.omit(riskscore)),"high","low"))
lung$risk <- risk

fit <- survfit(Surv(time, status) ~ risk, data = lung)
ggsurvplot(fit,
           conf.int = TRUE,
           risk.table.col = "strata", # Change risk table color by groups
           ggtheme = theme_bw(), # Change ggplot2 theme
           palette = c("green", "red"),
           xlim = c(0, 600),
           surv.median.line = "hv",  # add the median survival pointer.
           legend.labs = 
             c("Male", "Female"),    # change legend labels.
           pval = TRUE
)

ggsurvplot(fit,
           pval = TRUE, conf.int = TRUE,
           risk.table = TRUE, # Add risk table
           risk.table.col = "strata", # Change risk table color by groups
           linetype = "strata", # Change line type by groups
           surv.median.line = "hv", # Specify median survival
           ggtheme = theme_bw(), # Change ggplot2 theme
           palette = c("#FF6103", "#3D9140")

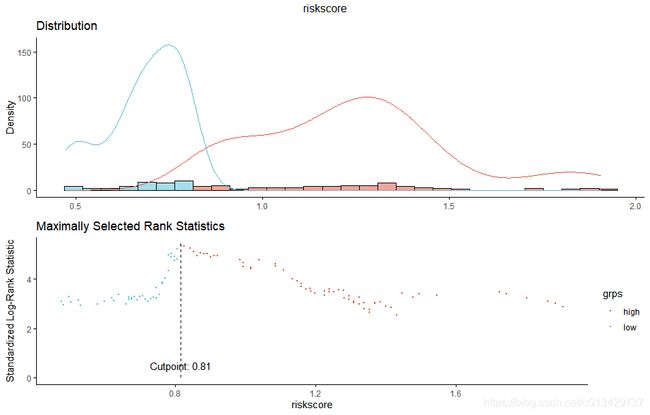
找一个最佳cut-off值。

riskscore=predict(res.cox,type="risk",newdata = lung)
lung$riskscore <- riskscore
fit <- survfit(Surv(time, status) ~ riskscore, data = lung)
summary(fit)
res.cut <- surv_cutpoint(lung, time = "time", event = "status",
                         variables = "riskscore")
summary(res.cut)
plot(res.cut, "riskscore", palette = "npg")

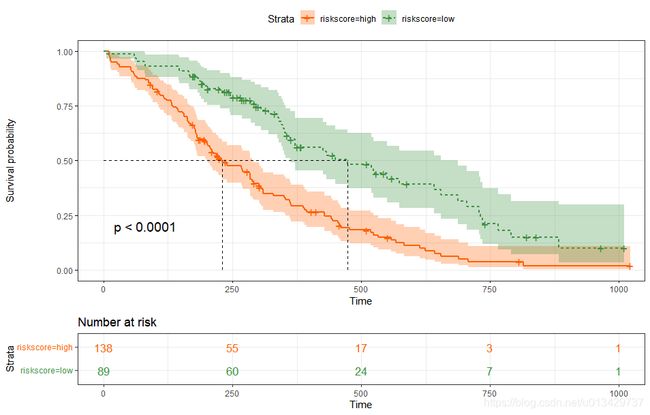
res.cat <- surv_categorize(res.cut)
fit <- survfit(Surv(time, status) ~riskscore, data = res.cat)
summary(fit)
ggsurvplot(fit,
           pval = TRUE, conf.int = TRUE,
           risk.table = TRUE, # Add risk table
           risk.table.col = "strata", # Change risk table color by groups
           linetype = "strata", # Change line type by groups
           surv.median.line = "hv", # Specify median survival
           ggtheme = theme_bw(), # Change ggplot2 theme
           palette = c("#FF6103", "#3D9140")
)

确实不一样了吧。

3、验证Cox回归模型有效性

验证Cox回归模型的有效性的基础是Schoenfeld残差的趋势检验。Schoenfeld残差的趋势检验法的基本思路是：如果proportional hazard model成立，拟合COX回归模型所得到的残差(即Schoenfeld残差)应该随时间在一条水平线上下波动，即残差与时间没有显著相关性。拟合残差与时间的线性函数，其斜率理论越接近0（也就是水平线） 。

# survival包的cox.zph()函数用来体现Schoenfeld残差与生存时间的关系
res.cox <- coxph(Surv(time, status) ~ age + sex + wt.loss, data =  lung)
test.ph <- cox.zph(res.cox)
> test.ph
            rho chisq     p
age     -0.0483 0.378 0.538
sex      0.1265 2.349 0.125
wt.loss  0.0126 0.024 0.877
GLOBAL       NA 2.846 0.416

# 可视化
ggcoxzph(test.ph)

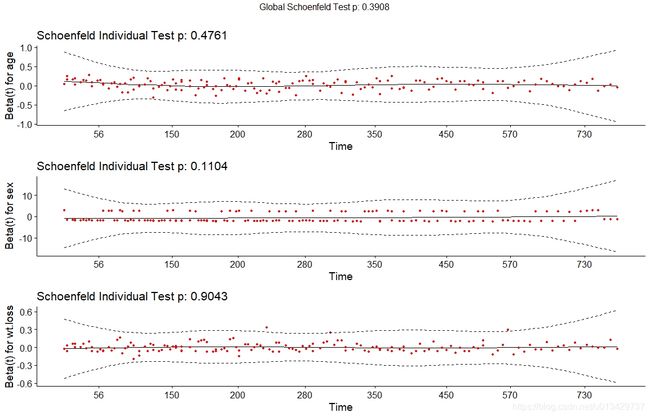
三个协方差均满足proportional hazards假设（如果曲线偏离2个标准差则表示不满足比例风险假定）

# 展示deviance residuals或者dfbeta values，体现异常值
ggcoxdiagnostics(res.cox, type = "dfbeta", linear.predictions = FALSE, ggtheme = theme_bw())

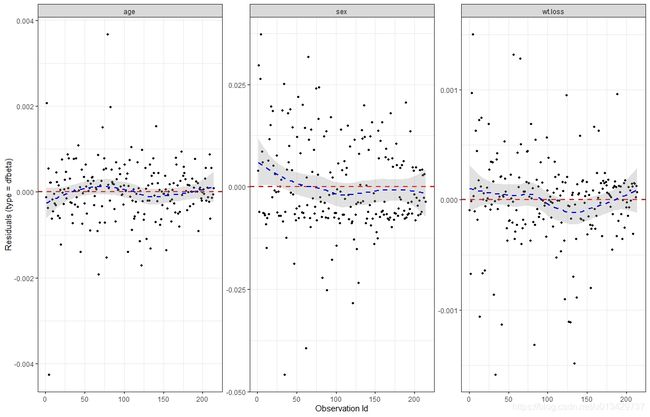
Positive values correspond to individuals that “died too soon” compared to expected survival times.
Negative values correspond to individual that “lived too long”.
Very large or small values are outliers, which are poorly predicted by the model.

ggcoxdiagnostics(res.cox, type = "deviance",
                 linear.predictions = FALSE, ggtheme = theme_bw())

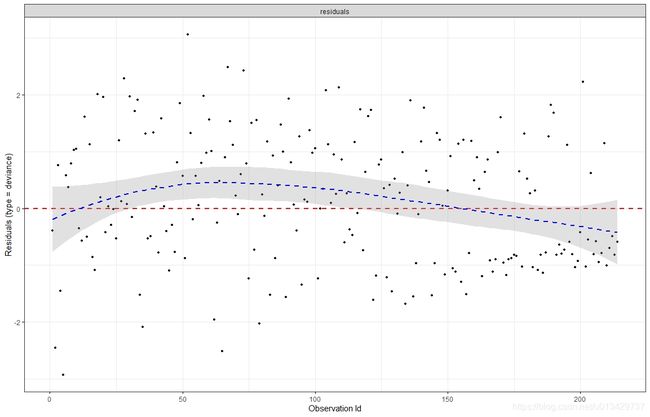
deviance残差一般以标准差为1对称分布在0附近，上图算是合格了。Deviance残差大于0，预测时间发生的时间比实际发生的时间早，模型高估风险。如果Deviance残差小于0，则预测事件发生的时间比实际发生的时间晚，模型低估风险。得分残差显示了删除某个观测后模型中系数变化的大小，变化越大，表示该观测样本对模型的影响越大。如果模型中很多观测的残差都较大，表明模型拟合的可能有问题。