【机器学习的数学基础】(六)矩阵分解(Matrix Decomposition)(上)
文章目录
-
- 4 矩阵分解(Matrix Decompositions)(上)
-
- 4.1 行列式与迹
- 4.2 特征值和特征向量
4 矩阵分解(Matrix Decompositions)(上)
在第2章和第3章中,我们研究了如何操作和度量向量以及向量的投影和线性映射。向量的映射和变换可以描述为由矩阵执行的操作。此外,矩阵还可以表示数据。例如,矩阵的行表示不同的人,列描述不同的人的特征,例如体重、身高和社会经济地位。在本章中,我们将介绍矩阵的三个方面:如何概括矩阵,如何分解矩阵,以及如何利用矩阵分解进行矩阵近似。
我们首先讨论用几个数字来描述矩阵的方法,这些数字代表了矩阵的整体性质。接着,我们将在行列式(第4.1节)和特征值(第4.2节)的章节中讨论方阵这一特殊情况。这些特征性的数代表重要的数学结论,使我们能够迅速了解到矩阵具有哪些有用的性质。然后我们将学习矩阵分解的方法:矩阵分解的一个类比是因数分解(factoring of numbers),例如将21分解成质数7·3。因此,矩阵分解也经常被称为matrix factorization。矩阵分解可以描述为:以矩阵作为因子,通过这些因子相乘表示另一个矩阵。
我们将首先讨论对称正定矩阵的类平方根运算,即Cholesky分解(第4.3节)。从这里我们将看到两个将矩阵分解成标准形式的相关方法。第一个是所谓的矩阵对角化(第4.4节),它允许我们使用对角变换矩阵来表示线性映射,前提是我们要选择一个合适的基。第二种方法是奇异值分解(第4.5节),将矩阵分解扩展到非方阵矩阵,它被认为是线性代数的基本概念之一。这些分解是很有用的,因为矩阵表示的数字数据通常非常大,很难分析。在本章的结尾,我们系统地概述了矩阵的类型以及划分矩阵类型的特征属性(第4.7节)。
本章所涉及的方法在随后的数学性的章节(如第6章)和应用性的章节(如第10章的降维或第11章的密度估计)中都很重要。图4.1的思维导图描述了本章的总体结构。
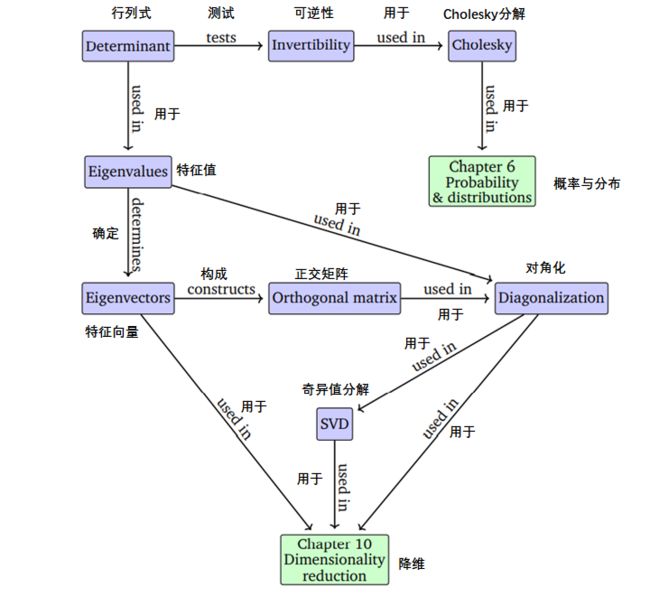
图 4.1本章介绍的概念的思维导图,以及它们在书的其他部分的应用。
4.1 行列式与迹
行列式是线性代数中的重要概念。行列式是分析和求解线性方程组的一个数学对象。行列式只适用于方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,即行数和列数相同的矩阵。在这本书中,我们把行列式写成 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A),有时写成 ∣ A ∣ | \boldsymbol{A} | ∣A∣(注意不要与绝对值混淆):
det ( A ) = ∣ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋱ ⋮ a n 1 a n 2 … a n n ∣ \operatorname{det}(\boldsymbol{A})=\left|\begin{array}{cccc}a_{11} & a_{12} & \ldots & a_{1 n} \\a_{21} & a_{22} & \ldots & a_{2 n} \\\vdots & & \ddots & \vdots \\a_{n 1} & a_{n 2} & \ldots & a_{n n}\end{array}\right| det(A)=∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22an2……⋱…a1na2n⋮ann∣∣∣∣∣∣∣∣∣
方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的行列式(determinant) 可以看作是将 A \boldsymbol{A} A映射到一个实数的函数。
在给出一般 n × n n×n n×n矩阵行列式的定义之前,让我们先看一些例子,并定义一些特殊矩阵的行列式。
例 4.1 矩阵可逆性检验
让我们从探讨方阵 A \boldsymbol{A} A是否可逆开始。我们已经知道如何判断最小的矩阵是否可逆了:如果 A \boldsymbol{A} A是一个 1 × 1 1\times 1 1×1的矩阵,即它是一个标量,那么 A = a ⟹ A − 1 = 1 a A=a \Longrightarrow A^{-1}=\frac{1}{a} A=a⟹A−1=a1,对于 a ≠ 0 a\not =0 a=0, a 1 a = 1 a \frac{1}{a}=1 aa1=1成立。
对于 2 × 2 2\times 2 2×2的矩阵,通过逆的定义(定义2.3),我们可以知道 A A − 1 = I \boldsymbol{A} \boldsymbol{A}^{-1}=\boldsymbol{I} AA−1=I。由公式(2. 24),我们知道 A \boldsymbol{A} A的逆为:
A − 1 = 1 a 11 a 22 − a 12 a 21 [ a 22 − a 12 − a 21 a 11 ] \boldsymbol{A}^{-1}=\frac{1}{a_{11} a_{22}-a_{12} a_{21}}\left[\begin{array}{cc}a_{22} & -a_{12} \\-a_{21} & a_{11}\end{array}\right] A−1=a11a22−a12a211[a22−a21−a12a11]
因此, A \boldsymbol{A} A可逆当且仅当:
a 11 a 22 − a 12 a 21 ≠ 0 a_{11} a_{22}-a_{12} a_{21} \neq 0 a11a22−a12a21=0
这个量就是 A ∈ R 2 × 2 \boldsymbol{A} \in \mathbb{R}^{2 \times 2} A∈R2×2的行列式,即:
det ( A ) = ∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \operatorname{det}(\boldsymbol{A})=\left|\begin{array}{ll}a_{11} & a_{12} \\a_{21} & a_{22}\end{array}\right|=a_{11} a_{22}-a_{12} a_{21} det(A)=∣∣∣∣a11a21a12a22∣∣∣∣=a11a22−a12a21
例4.1已经指出了行列式和逆矩阵存在性之间的关系。下面的定理将说明 n × n n×n n×n矩阵的相同结论。
定理 4.1
对于任意方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n当且仅当 det ( A ) ≠ 0 \operatorname{det}(\boldsymbol{A}) \neq 0 det(A)=0时, A \boldsymbol{A} A可逆。
对于小矩阵的行列式,我们有显式的表达式。如对于 n = 1 n=1 n=1,
det ( A ) = det ( a 11 ) = a 11 \operatorname{det}(\boldsymbol{A})=\operatorname{det}\left(a_{11}\right)=a_{11} det(A)=det(a11)=a11
对于 n = 2 n=2 n=2:
det ( A ) = ∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 ( 4.6 ) \operatorname{det}(\boldsymbol{A})=\left|\begin{array}{ll}a_{11} & a_{12} \\a_{21} & a_{22}\end{array}\right|=a_{11} a_{22}-a_{12} a_{21}\qquad (4.6) det(A)=∣∣∣∣a11a21a12a22∣∣∣∣=a11a22−a12a21(4.6)
对于 n = 3 n=3 n=3(被称为Sarrus’ rule):
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23 − a 31 a 22 a 13 − a 11 a 32 a 23 − a 21 a 12 a 33 ( 4.7 ) \begin{array}{l}\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right|=a_{11} a_{22} a_{33}+a_{21} a_{32} a_{13}+a_{31} a_{12} a_{23} \\\qquad\qquad\qquad\qquad-a_{31} a_{22} a_{13}-a_{11} a_{32} a_{23}-a_{21} a_{12} a_{33}\end{array}\qquad (4.7) ∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣=a11a22a33+a21a32a13+a31a12a23−a31a22a13−a11a32a23−a21a12a33(4.7)
如果对于 i > j i\gt j i>j, T i j = 0 \boldsymbol{T}_{ij}=0 Tij=0,即矩阵的对角线以下为零,则我们称 T \boldsymbol{T} T为上三角矩阵(upper-triangular matrix)。类似地,我们将下三角矩阵定义为在其对角线以上都为零的矩阵。对于一个三角矩阵 T ∈ R n × n \boldsymbol{T} \in \mathbb{R}^{n \times n} T∈Rn×n,其行列式是其对角元素的积:
det ( T ) = ∏ i = 1 n T i i \operatorname{det}(\boldsymbol{T})=\prod_{i=1}^{n} T_{i i} det(T)=i=1∏nTii
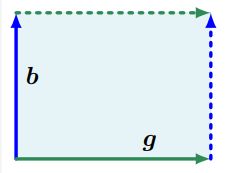
图4.2 由向量 b \boldsymbol{b} b和 g \boldsymbol{g} g张成的平行四边形(阴影区域)的面积为 ∣ det ( [ b , g ] ) ∣ |\operatorname{det}([\boldsymbol{b}, \boldsymbol{g}])| ∣det([b,g])∣。
例 4.2 行列式度量体积
当我们把行列式看作是一组 n n n个的向量(张成了 R n \mathbb{R}^{n} Rn中的一个对象)的映射时,它的概念很自然地表明行列式 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A)是由矩阵 A \boldsymbol{A} A的列构成的 n n n维平行六面体(平行六面体)的有符号体积。
对于 n = 2 n=2 n=2,矩阵的列形成平行四边形;如图4.2。随着向量之间的夹角变小,平行四边形的面积也会缩小。考虑构成矩阵 A = [ b , g ] \boldsymbol{A}=[\boldsymbol{b}, \boldsymbol{g}] A=[b,g]列的两个向量 b , g \boldsymbol{b}, \boldsymbol{g} b,g。那么, A \boldsymbol{A} A行列式的绝对值就是 0 , b , g , b + g \mathbf{0}, \boldsymbol{b}, \boldsymbol{g}, \boldsymbol{b}+\boldsymbol{g} 0,b,g,b+g围成的平行四边形的面积,特别地如果 b , g \boldsymbol{b}, \boldsymbol{g} b,g是线性相关的,即对于某些 λ ∈ R \lambda \in \mathbb{R} λ∈R, b = λ g \boldsymbol{b}=\lambda \boldsymbol{g} b=λg,它们就不再形成一个二维平行四边形了。因此相应的区域面积为0。相反,如果 b , g \boldsymbol{b}, \boldsymbol{g} b,g是线性独立的,并且是规范基向量 e 1 , e 2 \boldsymbol{e}_1, \boldsymbol{e}_2 e1,e2的倍数,那么它们可以写成 b = [ b 0 ] \boldsymbol{b}=\left[\begin{array}{l}b \\0\end{array}\right] b=[b0]和 g = [ 0 g ] \boldsymbol{g}=\left[\begin{array}{l}0 \\g\end{array}\right] g=[0g],其行列式是 ∣ b 0 0 g ∣ = b g − 0 = b g \left|\begin{array}{ll}b & 0 \\0 & g\end{array}\right|=b g-0=b g ∣∣∣∣b00g∣∣∣∣=bg−0=bg。
这就是我们熟悉的公式:面积=高度×长度。行列式的符号表示张成向量 b , g \boldsymbol{b}, \boldsymbol{g} b,g相对于标准基 ( e 1 , e 2 ) \left(\boldsymbol{e}_{1}, \boldsymbol{e}_{2}\right) (e1,e2)的方向。在我们的图4.2中,将向量顺序颠倒为 g \boldsymbol{g} g, b \boldsymbol{b} b即交换 A \boldsymbol{A} A的列和颠倒阴影区域的方向。(这里这本书讲的一般,推荐一个视频https://www.bilibili.com/video/BV1ys411472E?p=7 (05:07))
这可以延伸到更高的维度。在 R 3 \mathbb{R}^{3} R3中,我们考虑三个向量 r , b , g ∈ R 3 \boldsymbol{r}, \boldsymbol{b}, \boldsymbol{g} \in \mathbb{R}^{3} r,b,g∈R3,它们张成平行六面体的边,即各个面为平行四边形的实体,如图4.3。
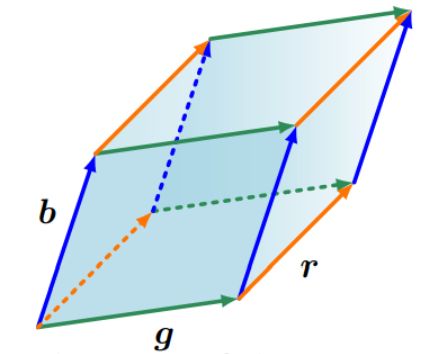
图4.3 由向量 r \boldsymbol{r} r, g \boldsymbol{g} g, b \boldsymbol{b} b张成的平行六面体(阴影区域)的体积为 ∣ det ( [ r , b , g ] ) ∣ |\operatorname{det}([\boldsymbol{r}, \boldsymbol{b}, \boldsymbol{g}])| ∣det([r,b,g])∣。
3 × 3 3×3 3×3矩阵 [ r , b , g ] [\boldsymbol{r}, \boldsymbol{b}, \boldsymbol{g}] [r,b,g]行列式的绝对值是六面体的体积。因此,行列式充当一个函数,用于测量由矩阵中的列向量构成的有符号体积。
考虑三个线性独立的向量 r , g , b ∈ R 3 \boldsymbol{r}, \boldsymbol{g}, \boldsymbol{b} \in \mathbb{R}^{3} r,g,b∈R3:
r = [ 2 0 − 8 ] , g = [ 6 1 0 ] , b = [ 1 4 − 1 ] \boldsymbol{r}=\left[\begin{array}{c}2 \\0 \\-8\end{array}\right], \quad \boldsymbol{g}=\left[\begin{array}{l}6 \\1 \\0\end{array}\right], \quad \boldsymbol{b}=\left[\begin{array}{c}1 \\4 \\-1\end{array}\right] r=⎣⎡20−8⎦⎤,g=⎣⎡610⎦⎤,b=⎣⎡14−1⎦⎤
把这些向量写成矩阵的列:
A = [ r , g , b ] = [ 2 6 1 0 1 4 − 8 0 − 1 ] \boldsymbol{A}=[\boldsymbol{r}, \boldsymbol{g}, \boldsymbol{b}]=\left[\begin{array}{ccc}2 & 6 & 1 \\0 & 1 & 4 \\-8 & 0 & -1\end{array}\right] A=[r,g,b]=⎣⎡20−861014−1⎦⎤
允许我们计算所需的体积:
V = ∣ det ( A ) ∣ = 186 V=|\operatorname{det}(\boldsymbol{A})|=186 V=∣det(A)∣=186
对于 n × n n×n n×n矩阵的行列式,需要一个通用的算法来解决 n > 3 n\gt 3 n>3的情况,我们将在下面探讨这个问题。定理4.2将计算 n × n n×n n×n矩阵的行列式的问题简化为计算 ( n − 1 ) × ( n − 1 ) (n−1)×(n−1) (n−1)×(n−1)矩阵的行列式。通过递归地应用拉普拉斯展开(定理 4.2),我们最终可以通过计算 2 × 2 2×2 2×2矩阵的行列式来计算 n × n n×n n×n矩阵的行列式。
定理 4.2 拉普拉斯展开 (Laplace Expansion)
考虑一个矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,那么,对于所有 j = 1 , … , n j=1, \ldots, n j=1,…,n,有:
1、 沿 j j j列扩展
det ( A ) = ∑ k = 1 n ( − 1 ) k + j a k j det ( A k , j ) \operatorname{det}(\boldsymbol{A})=\sum_{k=1}^{n}(-1)^{k+j} a_{k j} \operatorname{det}\left(\boldsymbol{A}_{k, j}\right) det(A)=k=1∑n(−1)k+jakjdet(Ak,j)
2、 沿 j j j行扩展
det ( A ) = ∑ k = 1 n ( − 1 ) k + j a j k det ( A j , k ) \operatorname{det}(\boldsymbol{A})=\sum_{k=1}^{n}(-1)^{k+j} a_{j k} \operatorname{det}\left(\boldsymbol{A}_{j, k}\right) det(A)=k=1∑n(−1)k+jajkdet(Aj,k)
这里, A k , j ∈ R ( n − 1 ) × ( n − 1 ) \boldsymbol{A}_{k, j} \in \mathbb{R}^{(n-1) \times(n-1)} Ak,j∈R(n−1)×(n−1)是 A \boldsymbol{A} A去除行 k k k和列 j j j后得到的子矩阵。
例 4.3 拉普拉斯展开
让我们计算
A = [ 1 2 3 3 1 2 0 0 1 ] \boldsymbol{A}=\left[\begin{array}{lll}1 & 2 & 3 \\3 & 1 & 2 \\0 & 0 & 1\end{array}\right] A=⎣⎡130210321⎦⎤
的行列式。沿着第一行使用拉普拉斯展开:
∣ 1 2 3 3 1 2 0 0 1 ∣ = ( − 1 ) 1 + 1 ⋅ 1 ∣ 1 2 0 1 ∣ + ( − 1 ) 1 + 2 ⋅ 2 ∣ 3 2 0 1 ∣ + ( − 1 ) 1 + 3 ⋅ 3 ∣ 3 1 0 0 ∣ \begin{aligned}\left|\begin{array}{lll}1 & 2 & 3 \\3 & 1 & 2 \\0 & 0 & 1\end{array}\right|=&(-1)^{1+1} \cdot 1\left|\begin{array}{ll}1 & 2 \\0 & 1\end{array}\right| \\&+(-1)^{1+2} \cdot 2\left|\begin{array}{ll}3 & 2 \\0 & 1\end{array}\right|+(-1)^{1+3} \cdot 3\left|\begin{array}{ll}3 & 1 \\0 & 0\end{array}\right|\end{aligned} ∣∣∣∣∣∣130210321∣∣∣∣∣∣=(−1)1+1⋅1∣∣∣∣1021∣∣∣∣+(−1)1+2⋅2∣∣∣∣3021∣∣∣∣+(−1)1+3⋅3∣∣∣∣3010∣∣∣∣
用(4.6)计算所有 2 × 2 2×2 2×2矩阵的行列式,得到:
det ( A ) = 1 ( 1 − 0 ) − 2 ( 3 − 0 ) + 3 ( 0 − 0 ) = − 5 \operatorname{det}(\boldsymbol{A})=1(1-0)-2(3-0)+3(0-0)=-5 det(A)=1(1−0)−2(3−0)+3(0−0)=−5
我们还可以将此结果与使用Sarrus规则(4.7)计算得到的结果进行比较:
det ( A ) = 1 ⋅ 1 ⋅ 1 + 3 ⋅ 0 ⋅ 3 + 0 ⋅ 2 ⋅ 2 − 0 ⋅ 1 ⋅ 3 − 1 ⋅ 0 ⋅ 2 − 3 ⋅ 2 ⋅ 1 = 1 − 6 = − 5 \operatorname{det}(\boldsymbol{A})=1 \cdot 1 \cdot 1+3 \cdot 0 \cdot 3+0 \cdot 2 \cdot 2-0 \cdot 1 \cdot 3-1 \cdot 0 \cdot 2-3 \cdot 2 \cdot 1=1-6=-5 det(A)=1⋅1⋅1+3⋅0⋅3+0⋅2⋅2−0⋅1⋅3−1⋅0⋅2−3⋅2⋅1=1−6=−5
对于 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,行列式具有以下特性:
- 矩阵相乘的行列式是相应行列式的乘积,即 det ( A B ) = det ( A ) det ( B ) \operatorname{det}(\boldsymbol{A B})=\operatorname{det}(\boldsymbol{A}) \operatorname{det}(\boldsymbol{B}) det(AB)=det(A)det(B)
- 矩阵转置不改变行列式的值,即 det ( A ) = det ( A ⊤ ) \operatorname{det}(\boldsymbol{A})=\operatorname{det}\left(\boldsymbol{A}^{\top}\right) det(A)=det(A⊤)
- 如果 A \boldsymbol{A} A是正则的(可逆的), det ( A − 1 ) = 1 det ( A ) \operatorname{det}\left(\boldsymbol{A}^{-1}\right)=\frac{1}{\operatorname{det}(\boldsymbol{A})} det(A−1)=det(A)1
- 相似矩阵(定义2. 22)具有相同的行列式。因此,对于线性映射 Φ : V → V \Phi: V \rightarrow V Φ:V→V, Φ \Phi Φ的所有变换矩阵 A Φ \boldsymbol{A}_{\Phi} AΦ都具有相同的行列式。因此,线性映射基的选择不影响行列式的值。
- 将一列/行的倍数添加到另一列/行不会更改 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A)。
- 用标量 λ ∈ R \lambda \in \mathbb{R} λ∈R乘矩阵 A \boldsymbol{A} A的行/列,将 λ \lambda λ倍缩放 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A)。特别地, det ( λ A ) = λ n det ( A ) \operatorname{det}(\lambda \boldsymbol{A})=\lambda^{n} \operatorname{det}(\boldsymbol{A}) det(λA)=λndet(A)
- 交换两行/列将更改 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A)的符号。
利用最后三个属性,我们可以使用高斯消去法通过将 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A)变换为行阶梯型来简化计算 det ( A ) \operatorname{det}(\boldsymbol{A}) det(A)。使用高斯消元法直到我们得到三角形矩阵,其对角线以下都是0。而三角形矩阵的行列式是对角线元素的乘积。
定理 4.3
一个方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的行列式 det ( A ) ≠ 0 \operatorname{det}(\boldsymbol{A}) \neq 0 det(A)=0,当且仅当 rk ( A ) = n \operatorname{rk}(\boldsymbol{A})=n rk(A)=n。换句话说, A \boldsymbol{A} A可逆当且仅当它是满秩的。
当人手工计算时,行列式计算被认为是分析矩阵可逆性的一种基本方法。然而,现代的机器学习方法使用直接的数值方法来代替行列式的显式计算。例如,在线性代数那一章中,我们了解到逆矩阵可以通过高斯消元法来计算。高斯消元法可以用来计算矩阵的行列式。
行列式将在以下章节中发挥重要的理论作用,特别是当我们通过特征多项式求解特征值和特征向量时。
定义 4.4
方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的迹(trace) 定义为:
tr ( A ) : = ∑ i = 1 n a i i \operatorname{tr}(\boldsymbol{A}):=\sum_{i=1}^{n} a_{i i} tr(A):=i=1∑naii
即,迹是 A \boldsymbol{A} A对角元素之和。
迹满足以下属性:
- 对于 A , B ∈ R n × n \boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{n \times n} A,B∈Rn×n, tr ( A + B ) = tr ( A ) + tr ( B ) \operatorname{tr}(\boldsymbol{A}+\boldsymbol{B})=\operatorname{tr}(\boldsymbol{A})+\operatorname{tr}(\boldsymbol{B}) tr(A+B)=tr(A)+tr(B)
- 对于 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n, tr ( α A ) = α tr ( A ) , α ∈ R \operatorname{tr}(\alpha \boldsymbol{A})=\alpha \operatorname{tr}(\boldsymbol{A}), \alpha \in \mathbb{R} tr(αA)=αtr(A),α∈R
- tr ( I n ) = n \operatorname{tr}\left(\boldsymbol{I}_{n}\right)=n tr(In)=n
- 对于 A ∈ R n × k , B ∈ R k × n \boldsymbol{A} \in \mathbb{R}^{n \times k}, \boldsymbol{B} \in \mathbb{R}^{k \times n} A∈Rn×k,B∈Rk×n, tr ( A B ) = tr ( B A ) \operatorname{tr}(\boldsymbol{A B})=\operatorname{tr}(\boldsymbol{B} \boldsymbol{A}) tr(AB)=tr(BA)
可以证明,只有一个函数同时满足这四个属性——迹(Gohberg et al., 2012)。
第四个属性更一般地,在循环置换下矩阵积的迹是不变的,即对于矩阵 A ∈ R a × k , K ∈ R k × l , L ∈ R l × a \boldsymbol{A} \in \mathbb{R}^{a \times k}, \boldsymbol{K} \in \mathbb{R}^{k \times l}, \boldsymbol{L} \in \mathbb{R}^{l \times a} A∈Ra×k,K∈Rk×l,L∈Rl×a:
tr ( A K L ) = tr ( K L A ) ( 4.19 ) \operatorname{tr}(\boldsymbol{A K} \boldsymbol{L})=\operatorname{tr}(\boldsymbol{K} \boldsymbol{L} \boldsymbol{A})\qquad (4.19) tr(AKL)=tr(KLA)(4.19)
这个性质可以推广到任意个矩阵的乘积。作为(4.19)的一个特例,对于两个向量 x , y ≡ R n \boldsymbol{x}, \boldsymbol{y} \equiv \mathbb{R}^{n} x,y≡Rn,有:
tr ( x y ⊤ ) = tr ( y ⊤ x ) = y ⊤ x ∈ R \operatorname{tr}\left(\boldsymbol{x} \boldsymbol{y}^{\top}\right)=\operatorname{tr}\left(\boldsymbol{y}^{\top} \boldsymbol{x}\right)=\boldsymbol{y}^{\top} \boldsymbol{x} \in \mathbb{R} tr(xy⊤)=tr(y⊤x)=y⊤x∈R
给定一个线性映射 Φ : V → V \Phi: V \rightarrow V Φ:V→V,其中 V V V为向量空间,我们定义映射 Φ \Phi Φ的迹为该映射的矩阵表示的迹。对于给定的 V V V的基,我们可以用变换矩阵 A \boldsymbol{A} A来描述 Φ \Phi Φ。那么 Φ \Phi Φ的迹就是 A \boldsymbol{A} A的迹。对于 V V V另一个不同的基, Φ Φ Φ相应的变换矩阵 B \boldsymbol{B} B可选取适当 S \boldsymbol{S} S,通过 S − 1 A S \boldsymbol{S}^{-1} \boldsymbol{A} \boldsymbol{S} S−1AS形式的基变换获得。对于 Φ Φ Φ相应的迹,有:
tr ( B ) = tr ( S − 1 A S ) = ( 4.19 ) tr ( A S S − 1 ) = tr ( A ) \operatorname{tr}(\boldsymbol{B})=\operatorname{tr}\left(\boldsymbol{S}^{-1} \boldsymbol{A} \boldsymbol{S}\right) \stackrel{(4.19)}{=} \operatorname{tr}\left(\boldsymbol{A} \boldsymbol{S} \boldsymbol{S}^{-1}\right)=\operatorname{tr}(\boldsymbol{A}) tr(B)=tr(S−1AS)=(4.19)tr(ASS−1)=tr(A)
因此,线性映射的矩阵表示依赖于基,而线性映射 Φ Φ Φ的迹独立于基。
在这一节中,我们将行列式和迹作为描述方阵的函数来讨论。结合我们对行列式和迹的理解,我们现在可以定义一个重要方程,用多项式来描述矩阵 A \boldsymbol{A} A,我们将在下面的部分中广泛使用它。
定义 5.5 特征多项式
对于 λ ∈ R \lambda \in \mathbb{R} λ∈R和一个方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,
p A ( λ ) : = det ( A − λ I ) = c 0 + c 1 λ + c 2 λ 2 + ⋯ + c n − 1 λ n − 1 + ( − 1 ) n λ n \begin{aligned}p_{\boldsymbol{A}}(\lambda) &:=\operatorname{det}(\boldsymbol{A}-\lambda \boldsymbol{I}) \\&=c_{0}+c_{1} \lambda+c_{2} \lambda^{2}+\cdots+c_{n-1} \lambda^{n-1}+(-1)^{n} \lambda^{n}\end{aligned} pA(λ):=det(A−λI)=c0+c1λ+c2λ2+⋯+cn−1λn−1+(−1)nλn
为特征多项式((Characteristic Polynomial))。其中 c 0 , … , c n − 1 ∈ R c_{0}, \ldots, c_{n-1} \in \mathbb{R} c0,…,cn−1∈R
特别地,
c 0 = det ( A ) c n − 1 = ( − 1 ) n − 1 tr ( A ) \begin{aligned}c_{0} &=\operatorname{det}(\boldsymbol{A}) \\c_{n-1} &=(-1)^{n-1} \operatorname{tr}(\boldsymbol{A})\end{aligned} c0cn−1=det(A)=(−1)n−1tr(A)
特征多项式将允许我们计算特征值和特征向量,这将在下一节中介绍。
4.2 特征值和特征向量
现在我们将了解一种新的方法来描述矩阵及其相关的线性映射。回想线性代数中2.71节的线性映射,给定一个有序基,线性映射都对应唯一的变换矩阵。我们可以通过“eigen”分析(eigen是一个德语单词,意思是“characteristic”、“self”或“own”。)来解释线性映射和相关的变换矩阵。正如我们将看到的,线性映射的特征值将告诉我们一组特殊的向量,即特征向量,是如何被线性映射转化得到的。
定义 4.6
令 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n为一个方阵。
A x = λ x \boldsymbol{A x}=\lambda \boldsymbol{x} Ax=λx
我们称这个方程为特征方程(eigenvalue equation)。其中 λ ∈ R \lambda \in \mathbb{R} λ∈R为 A \boldsymbol{A} A的特征值(eigenvalue), x ∈ R n \ { 0 } \boldsymbol{x} \in \mathbb{R}^{n} \backslash\{\mathbf{0}\} x∈Rn\{ 0}为相应的特征向量(eigenvector)。
备注:
在线性代数文献和软件中,通常有一种惯例,即特征值按降序排列,因此最大的特征值和相关的特征向量称为第一特征值和它的相关特征向量,第二大的特征值和相关的特征向量称为第二特征值和它的相关特征向量,依此类推。然而,教科书和出版物可能有不同或没有顺序的概念。如果没有明确说明,本书的特征值是无序的。
以下说法是等效的:
- λ \lambda λ是 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的特征值。
- 存在 x ∈ R n \ { 0 } \boldsymbol{x} \in \mathbb{R}^{n} \backslash\{\mathbf{0}\} x∈Rn\{ 0},使得 A x = λ x \boldsymbol{A x}=\lambda \boldsymbol{x} Ax=λx,或等价地, ( A − λ I n ) x = 0 (\boldsymbol{A}-\left.\lambda \boldsymbol{I}_{n}\right) \boldsymbol{x}=\mathbf{0} (A−λIn)x=0有非平凡解,即 x ≠ 0 \boldsymbol{x} \neq \mathbf{0} x=0
- rk ( A − λ I n ) < n \operatorname{rk}\left(\boldsymbol{A}-\lambda \boldsymbol{I}_{n}\right)\lt n rk(A−λIn)<n
- det ( A − λ I n ) = 0 \operatorname{det}\left(\boldsymbol{A}-\lambda \boldsymbol{I}_{n}\right)=0 det(A−λIn)=0
定义 4.7共线性和共向性
指向同一方向的两个向量称为共向的(codirected)。如果两个向量指向相同或相反的方向,则它们是共线的(collinear)。
备注:(特征向量的非唯一性)
如果 x \boldsymbol{x} x是 A \boldsymbol{A} A关于特征值 λ \lambda λ的特征向量。那么,对于任意 c ∈ R \ { 0 } c \in \mathbb{R} \backslash\{0\} c∈R\{ 0}, c x c\boldsymbol{x} cx是 A \boldsymbol{A} A的特征向量,且对应于相同的特征值,因为:
A ( c x ) = c A x = c λ x = λ ( c x ) \boldsymbol{A}(c \boldsymbol{x})=c \boldsymbol{A} \boldsymbol{x}=c \lambda \boldsymbol{x}=\lambda(c \boldsymbol{x}) A(cx)=cAx=cλx=λ(cx)
因此,与 x \boldsymbol{x} x共线的所有向量也是 A \boldsymbol{A} A的特征向量。
定理 4.8
λ ∈ R \lambda \in \mathbb{R} λ∈R为 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的特征值当且仅当 λ \lambda λ是 A \boldsymbol{A} A的特征方程 p A ( λ ) p_{A}(\lambda) pA(λ)的根。
定理 4.9
设方阵 A \boldsymbol{A} A有一个特征值 λ i \lambda_i λi。 λ i \lambda_i λi的代数重数( algebraic multiplicity) 是指根 λ i \lambda_i λi在特征多项式中出现的次数。
定理 4.10 特征空间和特征谱
对于 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n, A \boldsymbol{A} A对应于特征值 λ \lambda λ的特征向量集合张成 R n \mathbb{R}^{n} Rn的子空间,这个子空间称为 A \boldsymbol{A} A关于 λ \lambda λ的特征空间(eigenspace),记为: E λ E_{\lambda} Eλ。 A \boldsymbol{A} A的特征值构成的集合称为特征谱(eigenspectrum),或 A \boldsymbol{A} A的谱。
例 4.4 单位矩阵的情况
单位矩阵 I ∈ R n × n \boldsymbol{I} \in \mathbb{R}^{n \times n} I∈Rn×n的特征方程为 p I ( λ ) = det ( I − λ I ) = ( 1 − λ ) n = 0 p_{I}(\lambda)=\operatorname{det}(\boldsymbol{I}-\lambda \boldsymbol{I})=(1-\lambda)^{n}=0 pI(λ)=det(I−λI)=(1−λ)n=0,它只拥有 λ = 1 \lambda=1 λ=1这个特征值并出现 n n n次。而且,对于任意 x ∈ R n \ { 0 } \boldsymbol{x} \in \mathbb{R}^{n} \backslash\{\mathbf{0}\} x∈Rn\{ 0}, I x = λ x = 1 x \boldsymbol{I} \boldsymbol{x}=\lambda \boldsymbol{x}=1 \boldsymbol{x} Ix=λx=1x成立。因此,单位矩阵的唯一特征空间 E 1 E_1 E1张成 n n n维, R n \mathbb{R}^{n} Rn的 n n n个标准基向量都是 I \boldsymbol{I} I的特征向量。
关于特征值和特征向量的常用特性包括:
- 矩阵 A \boldsymbol{A} A及其转置 A ⊤ \boldsymbol{A}^{\top} A⊤具有相同的特征值,但不一定具有相同的特征向量。
- 特征空间 E λ E_{\lambda} Eλ是 A − λ I \boldsymbol{A}-\lambda \boldsymbol{I} A−λI的零空间,因为:
A x = λ x ⟺ A x − λ x = 0 ⟺ ( A − λ I ) x = 0 ⟺ x ∈ ker ( A − λ I ) \begin{aligned}\boldsymbol{A} \boldsymbol{x}=\lambda \boldsymbol{x} & \Longleftrightarrow \boldsymbol{A} \boldsymbol{x}-\lambda \boldsymbol{x}=\mathbf{0} \\& \Longleftrightarrow(\boldsymbol{A}-\lambda \boldsymbol{I}) \boldsymbol{x}=\mathbf{0} \Longleftrightarrow \boldsymbol{x} \in \operatorname{ker}(\boldsymbol{A}-\lambda \boldsymbol{I})\end{aligned} Ax=λx⟺Ax−λx=0⟺(A−λI)x=0⟺x∈ker(A−λI) - 相似矩阵(定义2.22)具有相同的特征值。基变换得到的是相似矩阵。因此,线性映射 Φ Φ Φ的特征值与它的变换矩阵的基的选择无关。这使得特征值、行列式和迹成为线性映射的关键特征参数,因为它们在基变化下都是不变的。
- 对称正定矩阵总是有正的实特征值。
例 4.5 计算特征值、特征向量和特征空间
求下面 2 × 2 2×2 2×2矩阵的特征值和特征向量
A = [ 4 2 1 3 ] \boldsymbol{A}=\left[\begin{array}{ll}4 & 2 \\1 & 3\end{array}\right] A=[4123]
Step 1 特征多项式
根据特征向量 x ≠ 0 x \neq 0 x=0和 A \boldsymbol{A} A的特征值 λ λ λ的定义,得到 A x = λ x \boldsymbol{A} \boldsymbol{x}=\lambda \boldsymbol{x} Ax=λx,即 ( A − λ I ) x = 0 (\boldsymbol{A}-\lambda \boldsymbol{I}) \boldsymbol{x}=\mathbf{0} (A−λI)x=0。由于 x ≠ 0 \boldsymbol{x} \neq 0 x=0,这要求 A − λ I \boldsymbol{A}-\lambda \boldsymbol{I} A−λI的核(零空间)包含其他元素而不只是 0 \boldsymbol{0} 0。这意味着 A − λ I \boldsymbol{A}-\lambda \boldsymbol{I} A−λI不可逆,即有 det ( A − λ I ) = 0 \operatorname{det}(\boldsymbol{A}-\lambda \boldsymbol{I})=0 det(A−λI)=0。因此,我们需要计算特征多项式的根来找到特征值。
Step 2 特征值
特征多项式为:
p A ( λ ) = det ( A − λ I ) = det ( [ 4 2 1 3 ] − [ λ 0 0 λ ] ) = ∣ 4 − λ 2 1 3 − λ ∣ = ( 4 − λ ) ( 3 − λ ) − 2 ⋅ 1 \begin{aligned}p_{A}(\lambda) &=\operatorname{det}(\boldsymbol{A}-\lambda \boldsymbol{I}) \\&=\operatorname{det}\left(\left[\begin{array}{ll}4 & 2 \\1 & 3\end{array}\right]-\left[\begin{array}{ll}\lambda & 0 \\0 & \lambda\end{array}\right]\right)=\left|\begin{array}{cc}4-\lambda & 2 \\1 & 3-\lambda\end{array}\right| \\&=(4-\lambda)(3-\lambda)-2 \cdot 1\end{aligned} pA(λ)=det(A−λI)=det([4123]−[λ00λ])=∣∣∣∣4−λ123−λ∣∣∣∣=(4−λ)(3−λ)−2⋅1
对特征多项式进行因式分解,得到
p ( λ ) = ( 4 − λ ) ( 3 − λ ) − 2 ⋅ 1 = 10 − 7 λ + λ 2 = ( 2 − λ ) ( 5 − λ ) p(\lambda)=(4-\lambda)(3-\lambda)-2 \cdot 1=10-7 \lambda+\lambda^{2}=(2-\lambda)(5-\lambda) p(λ)=(4−λ)(3−λ)−2⋅1=10−7λ+λ2=(2−λ)(5−λ)
得到根 λ 1 = 2 \lambda_1=2 λ1=2和 λ 2 = 5 \lambda_2=5 λ2=5
Step 3 特征向量与特征空间
我们通过观察向量 x \boldsymbol{x} x找到对应于这些特征值的特征向量,使得
[ 4 − λ 2 1 3 − λ ] x = 0 \left[\begin{array}{cc}4-\lambda & 2 \\1 & 3-\lambda\end{array}\right] \boldsymbol{x}=\mathbf{0} [4−λ123−λ]x=0
对于 λ = 5 \lambda=5 λ=5,我们得到:
[ 4 − 5 2 1 3 − 5 ] [ x 1 x 2 ] = [ − 1 2 1 − 2 ] [ x 1 x 2 ] = 0 \left[\begin{array}{cc}4-5 & 2 \\1 & 3-5\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right]=\left[\begin{array}{cc}-1 & 2 \\1 & -2\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right]=0 [4−5123−5][x1x2]=[−112−2][x1x2]=0
我们求解这个齐次方程组并得到一个解空间
E 5 = span [ [ 2 1 ] ] . E_{5}=\operatorname{span}[\left[\begin{array}{l}2 \\1\end{array}\right]]. E5=span[[21]].
这个特征空间是一维的,因为它只有一个基向量。
类似地,我们通过求解齐次方程组找到 λ = 2 λ=2 λ=2的特征向量
[ 4 − 2 2 1 3 − 2 ] x = [ 2 2 1 1 ] x = 0 \left[\begin{array}{cc}4-2 & 2 \\1 & 3-2\end{array}\right] \boldsymbol{x}=\left[\begin{array}{ll}2 & 2 \\1 & 1\end{array}\right] \boldsymbol{x}=\mathbf{0} [4−2123−2]x=[2121]x=0
这意味着对于任何 x 2 = − x 1 x_2=-x_1 x2=−x1的向量 x = [ x 1 x 2 ] \boldsymbol{x}=\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right] x=[x1x2],例如 [ 1 − 1 ] \left[\begin{array}{c}1 \\-1\end{array}\right] [1−1]是特征值2的特征向量。相应的特征空间如下所示
E 2 = span [ [ 1 − 1 ] ] E_{2}=\operatorname{span}[\left[\begin{array}{c}1 \\-1\end{array}\right]] E2=span[[1−1]]
例4.5中的两个特征空间 E 5 E_5 E5和 E 2 E_2 E2都是一维的,因为它们各自由一个向量张成。然而,在其他情况下,我们可能有多个相同的特征值(见定义4.9),则特征空间可能不止一维。
定义 4.11
设 λ i \lambda_i λi是方阵 A \boldsymbol{A} A的特征值,则 λ i \lambda_i λi的几何重数(geometric multiplicity) 是与 λ i \lambda_i λi对应的线性无关特征向量的个数。换句话说,它是由与 λ i \lambda_i λi对应的特征向量所张成的特征空间的维数。
备注:
一个特定的特征值的几何重数至少是一,因为每个特征值至少有一个对应的特征向量。特征值的几何重数不能超过其代数重数,但可以比它小。
例 4.6
矩阵 A = [ 2 1 0 2 ] A=\left[\begin{array}{ll}2 & 1 \\0 & 2\end{array}\right] A=[2012]有两个重复的特征值 λ 1 = λ 2 = 2 \lambda_1=\lambda_2=2 λ1=λ2=2,代数重数为2。这个特征值只有一个单位特征向量 x 1 = [ 1 0 ] \boldsymbol{x}_{1}=\left[\begin{array}{l}1 \\0\end{array}\right] x1=[10],所以它的几何重数为1。
.
图解行列式、特征向量和特征值:
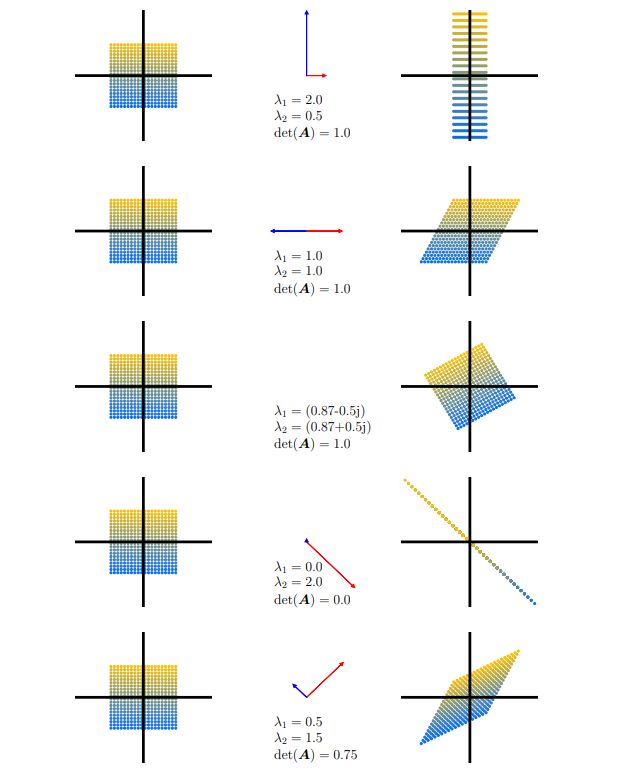
图 4.4 行列式和特征空间。五种线性映射及其相关变换矩阵 A i ∈ R 2 × 2 \boldsymbol{A}_i∈\mathbb{R}^{2×2} Ai∈R2×2的概述,它们将400个彩色编码点 x ∈ R 2 \boldsymbol{x}∈\mathbb{R}^2 x∈R2(左列)投影到目标点 A i x \boldsymbol{A}_i\boldsymbol{x} Aix(右列)上。中心列表示 第 一 特 征 向 量 \textcolor{blue}{第一特征向量} 第一特征向量,由其相关特征值 λ 1 λ_1 λ1拉伸; 第 二 特 征 向 量 \textcolor{red}{第二特征向量} 第二特征向量由其特征值 λ 2 λ_2 λ2拉伸。每行描述相对于标准基的五个变换矩阵 A i \boldsymbol{A}_i Ai中的一个的效果。
让我们用不同的线性映射来获得行列式、特征向量和特征值的一些直观感觉。下面展示了五个变换矩阵 A 1 , … , A 5 \boldsymbol{A}_{1}, \ldots, \boldsymbol{A}_{5} A1,…,A5对以原点为中心的正方形点网格的影响:
-
A 1 = [ 1 2 0 0 2 ] \boldsymbol{A}_{1}=\left[\begin{array}{ll}\frac{1}{2} & 0 \\0 & 2\end{array}\right] A1=[21002]。两个特征向量的方向与 R 2 \mathbb{R}^{2} R2中的标准基向量相同,即,在两个主轴上。纵轴延长2倍(特征值 λ 1 = 2 λ_1=2 λ1=2),横轴压缩 1 2 \frac{1}{2} 21倍(特征值 λ 2 = 1 2 λ_2=\frac{1}{2} λ2=21)。该映射不会改变原图形面积( det ( A 1 ) = 1 = 2 ⋅ 1 2 \operatorname{det}\left(\boldsymbol{A}_{1}\right)=1=2 \cdot \frac{1}{2} det(A1)=1=2⋅21)。

-
A 2 = [ 1 1 2 0 1 ] \boldsymbol{A}_{2}=\left[\begin{array}{ll}1 & \frac{1}{2} \\0 & 1\end{array}\right] A2=[10211]对应于剪切映射( shearing mapping),即,如果点位于垂直轴的正半轴,则沿水平轴向右剪切点,反之亦然。这个映射不改变原图形的面积( det ( A 2 ) = 1 \operatorname{det}\left(\boldsymbol{A}_{2}\right)=1 det(A2)=1)。特征值重复 λ 1 = 1 = λ 2 λ_1=1=λ_2 λ1=1=λ2,且特征向量共线(此处的绘制强调的是两个相反方向)。这表示映射仅沿一个方向(水平轴)起作用。

-
A 3 = [ cos ( π 6 ) − sin ( π 6 ) sin ( π 6 ) cos ( π 6 ) ] = 1 2 [ 3 − 1 1 3 ] \boldsymbol{A}_{3}=\left[\begin{array}{cc}\cos \left(\frac{\pi}{6}\right) & -\sin \left(\frac{\pi}{6}\right) \\\sin \left(\frac{\pi}{6}\right) & \cos \left(\frac{\pi}{6}\right)\end{array}\right]=\frac{1}{2}\left[\begin{array}{cc}\sqrt{3} & -1 \\1 & \sqrt{3}\end{array}\right] A3=[cos(6π)sin(6π)−sin(6π)cos(6π)]=21[31−13]。矩阵 A 3 \boldsymbol{A}_{3} A3将原图形的点逆时针旋转 π 6 r a d = 3 0 ∘ \frac{\pi}{6} \mathrm{rad}=30^{\circ} 6πrad=30∘,并且只有复数的特征值,这反映出映射是旋转(因此,没有绘制特征向量)。旋转必须保持体积不变,所以行列式是1。更多信息请回看解析几何。
- A 4 = [ 1 − 1 − 1 1 ] \boldsymbol{A}_{4}=\left[\begin{array}{cc}1 & -1 \\-1 & 1\end{array}\right] A4=[1−1−11]表示将二维域折叠到一维的标准基映射。由于有一个特征值为0,与 λ 1 = 0 λ_1=0 λ1=0对应的(蓝色)特征向量方向上的空间收缩为0,而与蓝色正交的(红色)特征向量将空间拉伸 λ 2 = 2 λ_2=2 λ2=2倍。因此,图像的面积为0。
- A 5 = [ 1 1 2 1 2 1 ] \boldsymbol{A}_{5}=\left[\begin{array}{ll}1 & \frac{1}{2} \\\frac{1}{2} & 1\end{array}\right] A5=[121211]是一种剪切和拉伸映射,它将空间缩放75%,因为 ∣ det ( A 5 ) ∣ = 3 4 \left|\operatorname{det}\left(A_{5}\right)\right|=\frac{3}{4} ∣det(A5)∣=43。它将空间沿 λ 2 λ_2 λ2的(红色)特征向量方向拉伸1.5倍,并沿与红色正交的(蓝色)特征向量方向压缩0.5倍。
定理 4.12
一个矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的 n n n个特征向量 x 1 , … , x n \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{n} x1,…,xn对应 n n n个不同的特征值 λ 1 , … , λ n \lambda_{1}, \ldots, \lambda_{n} λ1,…,λn,则它们是线性独立的。
这个定理指出,具有 n n n个不同特征值的矩阵的特征向量构成 R n \mathbb{R}^{n } Rn的基
定理 4.13
如果一个方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n具有少于 n n n个线性无关的特征向量,则它是亏损的(defective)。
非亏损矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n不一定需要 n n n个不同的特征值,但需要特征向量构成 R n \mathbb{R}^{n } Rn的基。从亏损矩阵的特征空间来看,特征空间的维数之和小于 n n n。具体地说,亏损矩阵至少有一个特征值 λ i λ_i λi,其代数重数 m > 1 m\gt 1 m>1,几何重数小于 m m m。
备注:
亏损矩阵不能有 n n n个不同的特征值,因为不同的特征值具有线性独立的特征向量(定理4.12)。
定理 4.14
给定一个矩阵 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n,我们总能通过
S : = A ⊤ A \boldsymbol{S}:=\boldsymbol{A}^{\top} \boldsymbol{A} S:=A⊤A
得到一个对称的半正定矩阵 S ∈ R n × n \boldsymbol{S} \in \mathbb{R}^{n \times n} S∈Rn×n:
备注:
如果 rk ( A ) = n \operatorname{rk}(\boldsymbol{A})=n rk(A)=n,那么 S : = A ⊤ A \boldsymbol{S}:=\boldsymbol{A}^{\top} \boldsymbol{A} S:=A⊤A是对称,正定的。
理解定理4.14成立的原因对我们应用对称矩阵很有帮助:对称矩阵要求 S = S T \boldsymbol{S}=\boldsymbol{S}^{\boldsymbol{T}} S=ST,由 S : = A ⊤ A \boldsymbol{S}:=\boldsymbol{A}^{\top} \boldsymbol{A} S:=A⊤A我们得到 S = A ⊤ A = A ⊤ ( A ⊤ ) ⊤ = ( A ⊤ A ) ⊤ = S ⊤ \boldsymbol{S}=\boldsymbol{A}^{\top} \boldsymbol{A}=\boldsymbol{A}^{\top}\left(\boldsymbol{A}^{\top}\right)^{\top}=\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{\top}=\boldsymbol{S}^{\top} S=A⊤A=A⊤(A⊤)⊤=(A⊤A)⊤=S⊤。而且,半正定矩阵要求 x ⊤ S x ⩾ 0 \boldsymbol{x}^{\top} \boldsymbol{S} \boldsymbol{x} \geqslant 0 x⊤Sx⩾0,由 S : = A ⊤ A \boldsymbol{S}:=\boldsymbol{A}^{\top} \boldsymbol{A} S:=A⊤A我们得到 x ⊤ S x = x ⊤ A ⊤ A x = ( x ⊤ A ⊤ ) ( A x ) = ( A x ) ⊤ ( A x ) ⩾ 0 \boldsymbol{x}^{\top} \boldsymbol{S} \boldsymbol{x}=\boldsymbol{x}^{\top} \boldsymbol{A}^{\top} \boldsymbol{A} \boldsymbol{x}=\left(\boldsymbol{x}^{\top} \boldsymbol{A}^{\top}\right)(\boldsymbol{A} \boldsymbol{x})=(\boldsymbol{A x})^{\top}(\boldsymbol{A} \boldsymbol{x}) \geqslant 0 x⊤Sx=x⊤A⊤Ax=(x⊤A⊤)(Ax)=(Ax)⊤(Ax)⩾0,因为点积计算的是平方和。
定理 4.15 谱定理
如果 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n是对称的,则存在 A \boldsymbol{A} A的特征向量组成对应向量空间 V V V的正交基,且每个特征值都是实数。
谱定理的直接含义是对称矩阵 A \boldsymbol{A} A的特征分解存在(具有实特征值),并且我们可以由特征向量得到标准正交基,使得 A \boldsymbol{A} A= P D P ⊤ \boldsymbol{P}\boldsymbol{D}\boldsymbol{P}^{\top} PDP⊤,其中 D \boldsymbol{D} D是对角的, P \boldsymbol{P} P的列为特征向量。
例 4.8
考虑矩阵
A = [ 3 2 2 2 3 2 2 2 3 ] \boldsymbol{A}=\left[\begin{array}{lll}3 & 2 & 2 \\2 & 3 & 2 \\2 & 2 & 3\end{array}\right] A=⎣⎡322232223⎦⎤
A \boldsymbol{A} A的特征方程为:
p A ( λ ) = − ( λ − 1 ) 2 ( λ − 7 ) p_{A}(\lambda)=-(\lambda-1)^{2}(\lambda-7) pA(λ)=−(λ−1)2(λ−7)
可以得到 λ 1 = 1 \lambda_1=1 λ1=1和 λ 2 = 7 \lambda_2=7 λ2=7,其中 λ 1 \lambda_1 λ1为复特征值。
按照我们计算特征向量的标准流程,可以得到对应的特征空间:
E 1 = span [ [ − 1 1 0 ] ⏟ = : x 1 [ − 1 0 1 ] ⏟ = : x 2 ] , E 7 = span [ [ 1 1 1 ] ⏟ = : x 3 ] E_{1}=\operatorname{span}[\underbrace{\left[\begin{array}{c}-1 \\1 \\0\end{array}\right]}_{=: \boldsymbol{x}_{1}} \underbrace{\left[\begin{array}{c}-1 \\0 \\1\end{array}\right]}_{=: x_{2}}], \quad E_{7}=\operatorname{span}[\underbrace{\left[\begin{array}{c}1 \\1 \\1\end{array}\right]}_{=: \boldsymbol{x}_{3}}] E1=span[=:x1 ⎣⎡−110⎦⎤=:x2 ⎣⎡−101⎦⎤],E7=span[=:x3 ⎣⎡111⎦⎤]
我们可以看到 x 3 \boldsymbol{x}_3 x3与 x 1 \boldsymbol{x}_1 x1和 x 2 \boldsymbol{x}_2 x2都正交。然而,由于 x 1 ⊤ x 2 = 1 ≠ 0 \boldsymbol{x}_{1}^{\top} \boldsymbol{x}_{2}=1 \neq 0 x1⊤x2=1=0,所以这两个向量不相互正交。我们所拥有的基不是正交的。但由谱定理(定理4.15)可知存在一个正交基,所以,我们可以构造一个。
为了构造这样一个基,我们利用特征向量 x 1 \boldsymbol{x}_1 x1, x 2 \boldsymbol{x}_2 x2对应同一特征值 λ λ λ这一事实,对于任何 α , β ∈ R \alpha, \beta \in \mathbb{R} α,β∈R,以下成立:
A ( α x 1 + β x 2 ) = A x 1 α + A x 2 β = λ ( α x 1 + β x 2 ) \boldsymbol{A}\left(\alpha \boldsymbol{x}_{1}+\beta \boldsymbol{x}_{2}\right)=\boldsymbol{A} \boldsymbol{x}_{1} \alpha+\boldsymbol{A} \boldsymbol{x}_{2} \beta=\lambda\left(\alpha \boldsymbol{x}_{1}+\beta \boldsymbol{x}_{2}\right) A(αx1+βx2)=Ax1α+Ax2β=λ(αx1+βx2)
即, x 1 \boldsymbol{x}_1 x1和 x 2 \boldsymbol{x}_2 x2的任何线性组合也是与 λ λ λ相关联的 A \boldsymbol{A} A的特征向量。
Gram-Schmidt算法是一种使用这种线性组合从一组基向量迭代构造正交/正交基的方法。因此,即使 x 1 \boldsymbol{x}_1 x1和 x 2 \boldsymbol{x}_2 x2不是正交的,我们也可以应用Gram-Schmidt算法(3.8.3节)找到与 λ 1 = 1 λ_1=1 λ1=1相关联的、彼此正交(并且与 x 3 \boldsymbol{x}_3 x3正交)的特征向量。在我们的例子中,我们可以得到
x 1 ′ = [ − 1 1 0 ] , x 2 ′ = 1 2 [ − 1 − 1 2 ] \boldsymbol{x}_{1}^{\prime}=\left[\begin{array}{c}-1 \\1 \\0\end{array}\right], \quad \boldsymbol{x}_{2}^{\prime}=\frac{1}{2}\left[\begin{array}{c}-1 \\-1 \\2\end{array}\right] x1′=⎣⎡−110⎦⎤,x2′=21⎣⎡−1−12⎦⎤
它们相互正交,且与 x 3 \boldsymbol{x}_{3} x3正交,且是 A \boldsymbol{A} A对应于 λ 1 = 1 λ_1=1 λ1=1的特征向量。
下面将特征值和特征向量与行列式和迹的概念联系起来。
定理 4.16
矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的行列式为其特征值的积
det ( A ) = ∏ i = 1 n λ i \operatorname{det}(\boldsymbol{A})=\prod_{i=1}^{n} \lambda_{i} det(A)=i=1∏nλi
其中 λ i ∈ C \lambda_{i} \in \mathbb{C} λi∈C(可重复)为 A \boldsymbol{A} A的特征值。
定理 4.17
矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的迹为其特征值的和
tr ( A ) = ∑ i = 1 n λ i \operatorname{tr}(\boldsymbol{A})=\sum_{i=1}^{n} \lambda_{i} tr(A)=i=1∑nλi
其中 λ i ∈ C \lambda_{i} \in \mathbb{C} λi∈C(可重复)为 A \boldsymbol{A} A的特征值。
图 4.6特征值的几何解释。 A \boldsymbol{A} A的特征向量被相应的特征值拉伸。单位正方形的面积变化 ∣ λ 1 λ 2 ∣ |λ_1λ_2| ∣λ1λ2∣倍,周长变化 1 2 ( ∣ λ 1 ∣ + ∣ λ 2 ∣ ) \frac{1}{2}(|λ_1| + |λ_2|) 21(∣λ1∣+∣λ2∣)倍。
让我们来看看这两个定理的几何直观解释。考虑一个矩阵 A ∈ R 2 × 2 \boldsymbol{A} \in \mathbb{R}^{2 \times 2} A∈R2×2拥有两个线性独立的特征向量 x 1 , x 2 \boldsymbol{x}_1,\boldsymbol{x}_2 x1,x2。对于这个例子,我们假设 ( x 1 , x 2 ) (\boldsymbol{x}_1,\boldsymbol{x}_2) (x1,x2)是 R 2 \mathbb{R}^{2} R2的标准正交基(ONB),它们所张成的正方形的面积是1;如图4.6所示。从第1节我们知道行列式计算单位方形面积在变换矩阵 A \boldsymbol{A} A下的变化。在这个例子中,我们可以明确地计算面积的变化:通过 A \boldsymbol{A} A对特征向量进行映射可以得到向量: v 1 = A x 1 = λ 1 x 1 \boldsymbol{v}_{1}=\boldsymbol{A} \boldsymbol{x}_{1}=\lambda_{1} \boldsymbol{x}_{1} v1=Ax1=λ1x1和 v 2 = A x 2 = λ 2 x 2 \boldsymbol{v}_{2}=\boldsymbol{A} \boldsymbol{x}_{2}=\lambda_{2} \boldsymbol{x}_{2} v2=Ax2=λ2x2,即新向量 v i \boldsymbol{v}_i vi是特征向量 x i \boldsymbol{x}_i xi的缩放版本,并且缩放因子是对应的特征值 λ i \lambda_i λi。 v 1 , v 2 \boldsymbol{v}_1,\boldsymbol{v}_2 v1,v2仍然是正交的,它们张成的矩形的面积是 ∣ λ 1 λ 2 ∣ |λ_1λ_2| ∣λ1λ2∣。
假设 x 1 , x 2 \boldsymbol{x}_1,\boldsymbol{x}_2 x1,x2(在我们的例子中)是正交的,我们可以直接计算单位方形的周长为 2 ( 1 + 1 ) 2(1+1) 2(1+1)。使用 A \boldsymbol{A} A映射特征向量将创建周长为 2 ( ∣ λ 1 ∣ + ∣ λ 2 ∣ ) 2\left(\left|\lambda_{1}\right|+\left|\lambda_{2}\right|\right) 2(∣λ1∣+∣λ2∣)的矩形。因此,特征值的绝对值之和告诉我们单位方形的周长在变换矩阵 A \boldsymbol{A} A下是如何变化的。
翻译自:
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth,A Aldo Faisal 和 Cheng Soon Ong
公众号后台回复【m4ml】即可获取这本书。
另外,机器学习的数学基础.pdf


