小识 神经网络的初始化
如有转载,请标明出处
初始化的原因
对于一个神经网络而言,我们自然希望它是鲁棒的。也就是说,对于任何一个初始化的点,我们都能得到比较好的收敛结果。不幸的是,几乎所有的网络都是非凸的,不同的初始化得到的结果可能大相径庭。
而且,如果权重初始化的方差过大或过小,可能会导致梯度爆炸或梯度弥散的问题,从而无法收敛。
因此,合适的权重初始化就尤为重要。
目前存在以下几种初始化策略:
- Constant Initialization
- Xavier Initialization
- Kaiming Initialization
Constant Initialization
一般来说,就是将权重设置为全0的矩阵。通常来讲,这样效果不好。因为这意味着所有的单元初始化为完全相同的状态,会导致同层的每个神经元的前向与反向传播存在某种对称关系甚至完全相同,这样的话,同层的神经元就学不到更多的信息,致使其效果不佳。
Xavier Initialization
除却常数初始化外,还有将参数初始化为 W ∼ N ( 0 , 1 ) W \sim N(0,1) W∼N(0,1) ,但随着神经网络深度的增加,此方法不能解决梯度消失的问题。如下图所示:
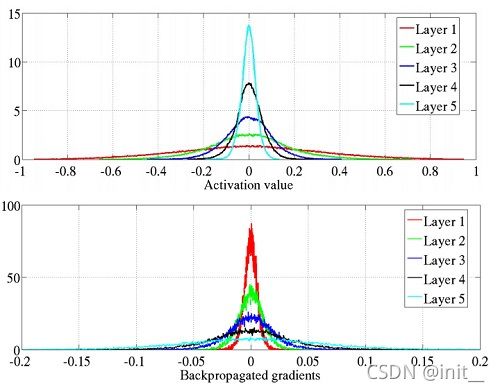
为了解决上述问题,Xavier的作者提出一种使方差在传播时保持不变的方案。
如前文所述,其理论是在全连接层的情况下,那么,有:
Y = W X + B Y = WX+B Y=WX+B
前向计算
需要满足: v a r ( Y ) = v a r ( X ) var(Y)=var(X) var(Y)=var(X)
假设权重数值之间是独立同分布的, X X X 数值之间也是独立同分布的, 且 X X X和权重相互独立。且bias为0,W满足均值为0 的某种高斯分布。
其中, d d d 是 输入向量的维度。若要实现 V a r ( Y i ) = V a r ( X j ) Var(Y_i)=Var(X_j) Var(Yi)=Var(Xj),则必须满足 d × V a r ( W i j ) = 1 d\times Var(W_{ij})=1 d×Var(Wij)=1 ,即: V a r ( W i j ) = 1 d Var(W_{ij})=\frac{1}{d} Var(Wij)=d1 ,进一步得出初始化方式:
- 若 W i j W_{ij} Wij服从正态分布,则 W i j ∼ N o r m a l ( 0 , 1 d ) W_{ij}\sim Normal(0,\frac{1}{d}) Wij∼Normal(0,d1);
- 若 W i j W_{ij} Wij服从均匀分布,则 W i j ∼ U n i f o r m ( − 3 d , 3 d ) W_{ij}\sim Uniform(-\sqrt{\frac{3}{d}},\sqrt{\frac{3}{d}}) Wij∼Uniform(−d3,d3);
后向计算
△ X = W T △ Y \bigtriangleup X=W^T\bigtriangleup Y △X=WT△Y
其中, w ∈ R u × d w\in \mathbb{R}^{u\times d} w∈Ru×d, △ y ∈ R u \bigtriangleup y\in \mathbb{R}^u △y∈Ru, △ x ∈ R d \bigtriangleup x\in \mathbb{R}^d △x∈Rd。
若要做到后向计算信号强度不变,就需要满足: V a r ( △ X j ) = V a r ( △ Y i ) Var(\bigtriangleup X_j)=Var(\bigtriangleup Y_i) Var(△Xj)=Var(△Yi)。
同样的道理,我们有 u × V a r ( W i j ) = 1 u\times Var(W_{ij})=1 u×Var(Wij)=1,即 V a r ( W i j ) = 1 u Var(W_{ij})=\frac{1}{u} Var(Wij)=u1,那么其初始化方式为:
- 若 W i j W_{ij} Wij服从正态分布,则 W i j ∼ N o r m a l ( 0 , 1 u ) W_{ij}\sim Normal(0,\frac{1}{u}) Wij∼Normal(0,u1);
- 若 W i j W_{ij} Wij服从均匀分布,则 W i j ∼ U n i f o r m ( − 3 u , 3 u ) W_{ij}\sim Uniform(-\sqrt{\frac{3}{u}},\sqrt{\frac{3}{u}}) Wij∼Uniform(−u3,u3);
调和平均
根据上面的推导可以看出,除非 d = u d=u d=u,否则我们无法同时保证前后向信号的Variance不发生变化,所以原论文中对 V a r ( W i j Var(W_{ij} Var(Wij取了一个调和平均数: V a r ( W j i ) = 2 d + u Var(W_{ji})=\frac{2}{d+u} Var(Wji)=d+u2,进一步得到模型初始化方式:
- 若 W i j W_{ij} Wij服从正态分布,则 W i j ∼ N o r m a l ( 0 , 2 d + u ) W_{ij}\sim Normal(0,\frac{2}{d+u}) Wij∼Normal(0,d+u2);
- 若 W i j W_{ij} Wij服从均匀分布,则 W i j ∼ U n i f o r m ( − 6 d + u , 6 d + u ) W_{ij}\sim Uniform(-\sqrt{\frac{6}{d+u}},\sqrt{\frac{6}{d+u}}) Wij∼Uniform(−d+u6,d+u6);
缺陷
Xavier初始化的问题在于,其初始化的假设中没有激活函数。但实际上,激活函数是深度神经网络中不可或缺的一部分,而Xavier初始化的结果经过ReLU后结果发生了偏移,因此,何凯明大神提出了Kaiming初始化。
Kaiming Initialization
torch.nn.init中封装了Kaiming初始化。
torch.nn.init.kaiming_uniform_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’)Fills the input Tensor with values according to the method described in Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification - He, K. et al. (2015), using a uniform distribution. The resulting tensor will have values sampled from $\mathcal{U}(-\text{bound}, \text{bound}) $ where
b o u n d = g a i n × 3 f a n _ m o d e bound = gain \times \sqrt{\frac{3}{fan\_mode}} bound=gain×fan_mode3
torch.nn.init.``kaiming_normal_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’)Fills the input Tensor with values according to the method described in Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification - He, K. et al. (2015), using a normal distribution. The resulting tensor will have values sampled from N ( 0 , s t d 2 ) N(0,std^2) N(0,std2) where
s t d = g a i n f a n _ m o d e std = \frac {gain}{fan\_mode} std=fan_modegain
方差的计算需要两个值:gain 和 fan。 gain 值由激活函数决定. fan 值由权重参数的数量和传播的方向决定. fan_in 表示前向传播, fan_out 表示反向传播。
来点源码调节一下心情。
# 根据网络设计时卷积权重的形状和前向传播还是反向传播, 进行 fan 值的计算。
def _calculate_fan_in_and_fan_out(tensor):
dimensions = tensor.dim() # 返回的是维度
if dimensions < 2:
raise ValueError("Fan in and fan out can not be computed for tensor with fewer than 2 dimensions")
if dimensions == 2: # Linear
fan_in = tensor.size(1)
fan_out = tensor.size(0)
else:
num_input_fmaps = tensor.size(1) # 卷积的输入通道大小
num_output_fmaps = tensor.size(0) # 卷积的输出通道大小
receptive_field_size = 1
if tensor.dim() > 2:
receptive_field_size = tensor[0][0].numel() # 卷积核的大小:k*k
fan_in = num_input_fmaps * receptive_field_size # 输入通道数量*卷积核的大小. 用于前向传播
fan_out = num_output_fmaps * receptive_field_size # 输出通道数量*卷积核的大小. 用于反向传播
return fan_in, fan_out
def _calculate_correct_fan(tensor, mode):
mode = mode.lower()
valid_modes = ['fan_in', 'fan_out']
if mode not in valid_modes:
raise ValueError("Mode {} not supported, please use one of {}".format(mode, valid_modes))
fan_in, fan_out = _calculate_fan_in_and_fan_out(tensor)
return fan_in if mode == 'fan_in' else fan_out
def calculate_gain(nonlinearity, param=None):
r"""Return the recommended gain value for the given nonlinearity function.
The values are as follows:
================= ====================================================
nonlinearity gain
================= ====================================================
Linear / Identity :math:`1`
Conv{1,2,3}D :math:`1`
Sigmoid :math:`1`
Tanh :math:`\frac{5}{3}`
ReLU :math:`\sqrt{2}`
Leaky Relu :math:`\sqrt{\frac{2}{1 + \text{negative\_slope}^2}}`
================= ====================================================
Args:
nonlinearity: the non-linear function (`nn.functional` name)
param: optional parameter for the non-linear function
Examples:
>>> gain = nn.init.calculate_gain('leaky_relu', 0.2) # leaky_relu with negative_slope=0.2
"""
linear_fns = ['linear', 'conv1d', 'conv2d', 'conv3d', 'conv_transpose1d', 'conv_transpose2d', 'conv_transpose3d']
if nonlinearity in linear_fns or nonlinearity == 'sigmoid':
return 1
elif nonlinearity == 'tanh':
return 5.0 / 3
elif nonlinearity == 'relu':
return math.sqrt(2.0)
elif nonlinearity == 'leaky_relu':
if param is None:
negative_slope = 0.01
elif not isinstance(param, bool) and isinstance(param, int) or isinstance(param, float):
# True/False are instances of int, hence check above
negative_slope = param
else:
raise ValueError("negative_slope {} not a valid number".format(param))
return math.sqrt(2.0 / (1 + negative_slope ** 2))
else:
raise ValueError("Unsupported nonlinearity {}".format(nonlinearity))
回到正题,现在我们一起来研究一下Kaiming初始化的推导过程。
推导
kaiming 初始化的推导过程只包含卷积和 ReLU 激活函数, 默认是 vgg 类似的网络, 没有残差, concat 之类的结构, 也没有 BN 层.
Y l = W l X l + B l Y_l = W_lX_l+B_l Yl=WlXl+Bl
前向传播
v a r ( y l ) = n l v a r ( w l x l ) var(y_l) = n_l var(w_l x_l) var(yl)=nlvar(wlxl)
由于, w l , x l w_l, x_l wl,xl相互独立,有:
v a r ( y l ) = n l [ v a r ( w l ) v a r ( x l ) + v a r ( w l ) ( E x l ) 2 + ( E w l ) 2 v a r ( x l ) ] var(y_l)=n_l[var(w_l)var(x_l)+var(w_l)(Ex_l)^2+(Ew_l)^2var(x_l)] var(yl)=nl[var(wl)var(xl)+var(wl)(Exl)2+(Ewl)2var(xl)]
初始化的时候令权重的均值是 0, 且假设更新的过程中权重的均值一直是 0, 那么有 E ( w l ) = 0 E(w_l)=0 E(wl)=0,但是 x l x_l xl经过了ReLU,所以有:
v a r ( y l ) = n l [ v a r ( w l ) v a r ( x l ) + v a r ( w l ) ( E x l ) 2 ] = n l v a r ( w l ) ( v a r ( x l ) + ( E x l ) 2 ) var(y_l)=n_l[var(w_l)var(x_l)+var(w_l)(Ex_l)^2]=n_lvar(w_l)(var(x_l)+(Ex_l)^2) var(yl)=nl[var(wl)var(xl)+var(wl)(Exl)2]=nlvar(wl)(var(xl)+(Exl)2)
由于: v a r ( X ) = E ( X 2 ) − ( E X ) 2 var(X)=E(X^2)-(EX)^2 var(X)=E(X2)−(EX)2
那么有: v a r ( y l ) = n l v a r ( w l ) E ( x l 2 ) var(y_l)=n_lvar(w_l)E(x^2_l) var(yl)=nlvar(wl)E(xl2)
通过第l-1层的输出来计算该期望,我们有 x l = f ( y l − 1 ) x_l=f(y_{l-1}) xl=f(yl−1),其中f是relu
E ( x l 2 ) = E ( f 2 ( y l − 1 ) ) = ∫ − ∞ + ∞ p ( y l − 1 ) f 2 ( y l − 1 ) d y l − 1 E(x^2_l)=E(f^2(y_{l-1}))=\int_{- \infty}^{+ \infty} p(y_{l-1})f^2(y_{l-1})dy_{l-1} E(xl2)=E(f2(yl−1))=∫−∞+∞p(yl−1)f2(yl−1)dyl−1
由于relu的特性,我们可得:
E ( x l 2 ) = E ( f 2 ( y l − 1 ) ) = ∫ 0 + ∞ p ( y l − 1 ) ( y l − 1 ) 2 d y l − 1 E(x^2_l)=E(f^2(y_{l-1}))=\int_{0}^{+ \infty} p(y_{l-1})(y_{l-1})^2dy_{l-1} E(xl2)=E(f2(yl−1))=∫0+∞p(yl−1)(yl−1)2dyl−1
现因 w l − 1 w_{l−1} wl−1 是假设在 0 周围对称分布且均值为 0, 所以 y l − 1 y_{l-1} yl−1 也是在 0 附近分布是对称的, 并且均值为 0(此处假设偏置为 0
E ( x l 2 ) = E ( f 2 ( y l − 1 ) ) = 1 2 ( ∫ 0 + ∞ p ( y l − 1 ) ( y l − 1 ) 2 d y l − 1 + ∫ − ∞ 0 p ( y l − 1 ) ( y l − 1 ) 2 d y l − 1 ) = 1 2 ∫ − ∞ + ∞ p ( y l − 1 ) ( y l − 1 ) 2 d y l − 1 = 1 2 E ( y l − 1 2 ) E(x^2_l)=E(f^2(y_{l-1}))=\frac{1}{2}(\int_{0}^{+ \infty} p(y_{l-1})(y_{l-1})^2dy_{l-1}+\int_{- \infty}^{0} p(y_{l-1})(y_{l-1})^2dy_{l-1})=\frac{1}{2} \int_{- \infty}^{+ \infty}p(y_{l-1})(y_{l-1})^2dy_{l-1}=\frac{1}{2}E(y^2_{l-1}) E(xl2)=E(f2(yl−1))=21(∫0+∞p(yl−1)(yl−1)2dyl−1+∫−∞0p(yl−1)(yl−1)2dyl−1)=21∫−∞+∞p(yl−1)(yl−1)2dyl−1=21E(yl−12)
又 E ( y l − 1 ) = 0 E(y_{l-1})=0 E(yl−1)=0,有:
E ( x l 2 ) = 1 2 E ( y l − 1 2 ) = 1 2 v a r ( y l − 1 ) E(x^2_l)=\frac{1}{2}E(y^2_{l-1})=\frac{1}{2}var(y_{l-1}) E(xl2)=21E(yl−12)=21var(yl−1)
带入原式,我们有:
v a r ( y l ) = 1 2 n l v a r ( w l ) v a r ( y l − 1 ) var(y_{l})=\frac{1}{2}n_lvar(w_{l})var(y_{l-1}) var(yl)=21nlvar(wl)var(yl−1)
易知:
v a r ( y l ) = v a r ( y 1 ) ( ∏ i = 0 L 1 2 n l v a r ( w l ) ) var(y_{l})=var(y_{1})(\displaystyle\prod_{i=0}^L\frac{1}{2}n_lvar(w_l)) var(yl)=var(y1)(i=0∏L21nlvar(wl))
为了让每层的方差相同,则有:
1 2 n l v a r ( w l ) = 1 \frac{1}{2}n_lvar(w_l)=1 21nlvar(wl)=1
v a r ( w l ) = 2 n l var(w_l)=\frac{2}{n_l} var(wl)=nl2
得到如下结论:
-
W i , j ∼ N ( 0 , 2 n l ) W_{i,j} \sim N(0,\frac{2}{n_l}) Wi,j∼N(0,nl2) Or
-
W i , j ∼ U ( − 6 n l , 6 n l ) W_{i,j} \sim U(-\sqrt{\frac{6}{n_l}},\sqrt{\frac{6}{n_l}}) Wi,j∼U(−nl6,nl6)
反向传播
后向传播与前向传播的推导过程类似,这里就不赘述。
得到如下结论:
- W i , j ∼ N ( 0 , 2 n l + 1 ) W_{i,j} \sim N(0,\frac{2}{n_{l+1}}) Wi,j∼N(0,nl+12) Or
- W i , j ∼ U ( − 6 n l + 1 , 6 n l + 1 ) W_{i,j} \sim U(-\sqrt{\frac{6}{n_{l+1}}},\sqrt{\frac{6}{n_{l+1}}}) Wi,j∼U(−nl+16,nl+16)
参考文献
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
Understanding the difficulty of training deep feedforward neural networks
