集成学习task7 投票法的原理和案例分析

参考来源：

1. https://github.com/datawhalechina/team-learning-data-mining/tree/master/EnsembleLearning
2. https://zhuanlan.zhihu.com/p/27689464
3. 《机器学习》，周志华 ，清华大学出版社

1. 集成学习

在上一期组队学习关于深度学习推荐系统的过程中我们发现，很多推荐系统都使用了几个不同模型的组合用于处理不同类别的输入特征。比如使用embedding解决稀疏向量的问题，使用DNN来处理高维特征等等。而在学习机器学习的过程中，每个机器学习方法都有其特点和优势，能否将机器学习也进行类似的组合，达到取长补短的目的呢？这就是集成学习的思路了。

集成学习（ensemble Learning）通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统（multi-classifier system）、基于委员会的学习（committee-bassed learning）等。

如图所示，显示出集成学习的一般结构：先产生一组“个体学习器”（individual learner），再用某种策略将它们结合起来。个体学习器通常由一个现有的学习算法从训练数据产生，例如C4.5决策树算法、BP神经网络算法等，此时集成学中只包含同种类型的个体学习器，如“决策树集成”中全是决策树，“神经网络集成”中全是神经网络。这样的集成是“同质”的（homogeneous）。同质集成中的个体学习器亦称“基学习器（base learner）”，相应的想学习算法称为“基学习算法”（base learning alogrithm）。集成学习也可包含不同类型的个体学习器，例如包含决策树和神经网络，这样的集成是“异质（heterogenous）”的。异质集成中的个体学习器由不同的学习算法生成，这时就不再有基学习算法；相应的，个体学习器一般不称为基学习器，常称为“组件学习器”（component learner）或直接称为个体学习器。

集成学习通过将多个学习器进行结合，常可获得比单一学习器显著优越的泛化性能。这对“弱学习器”（weak learner）尤为明显，因此集成学习的很多理论研究都是针对弱学习器进行的，而基学习器有时也被直接称为弱学习器。但需注意的是，虽然从理论上来说使用弱学习器集成足以获得好的性能，但在实践中出于种种考虑，例如希望使用较少的个体学习器，或重用关于常见学习器的一些经验等，人们往往会使用比较强的学习器。

弱学习器常指泛化性能略由于随机猜测的学习器；例如在二分类问题上精度略高于50%

根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类，即个体学习器之间存在强依赖关系、必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系、可同时生成的并行化方法；前者的代表是Boosting，后者的代表是Bagging和“随机森林”（Random Forest）。

2. 投票法的思路

引用自：https://github.com/datawhalechina/team-learning-data-mining/blob/master/EnsembleLearning/CH3-%E9%9B%86%E6%88%90%E5%AD%A6%E4%B9%A0%E4%B9%8B%E6%8A%95%E7%A5%A8%E6%B3%95%E4%B8%8Ebagging/%E9%9B%86%E6%88%90%E5%AD%A6%E4%B9%A0%E7%AC%AC%E4%B8%89%E7%AB%A0.markdown

投票法是集成学习中常用的技巧，可以帮助我们提高模型的泛化能力，减少模型的错误率。举个例子，在航空航天领域，每个零件发出的电信号都对航空器的成功发射起到重要作用。如果我们有一个二进制形式的信号：

11101100100111001011011011011

在传输过程中第二位发生了翻转

10101100100111001011011011011

这导致的结果可能是致命的。一个常用的纠错方法是重复多次发送数据，并以少数服从多数的方法确定正确的传输数据。一般情况下，错误总是发生在局部，因此融合多个数据是降低误差的一个好方法，这就是投票法的基本思路。

对于回归模型来说，投票法最终的预测结果是多个其他回归模型预测结果的平均值。

对于分类模型，硬投票法的预测结果是多个模型预测结果中出现次数最多的类别，软投票对各类预测结果的概率进行求和，最终选取概率之和最大的类标签。

3. 投票法的原理

投票法在回归和分类模型上均可使用。在回归模型时，预测结果是所有模型预测结果的平均值；在分类模型时，预测结果是所有模型出现种类最多的结果。

而投票法用在分类模型上又可以分为硬投票与软投票，硬投票的方法是，取所有分类器投票结果最多的类，软投票的方法是预测结果是所有投票结果中概率最大的类。

硬投票就好像美国大选，每个州是一个分类器，这个分类器中，谁取得了50%以上的票数，该州所有票都给那个人。
软投票就好像全民普选，最终结果是所有人票数的加和，而不是“选举人”方法。

举个栗子吧，我们现在有三个二分类器，分别会分成A，B两种结果，对于每个样本，每个分类器的结果如下：

• 分类器1：有60%的可能性是A，40%的可能性是B
• 分类器2：有51%的可能性是A，49%的可能性是B
• 分类器3：有20%的可能性是A，80%的可能性是B

如果根据硬投票方法，1和2的预测结果都是A，则投票法的预测结果就是A。若根据软投票方法，预测为A的平均概率为(60%+51%+20%)/3=43.67%，预测为B的平均概率为56.33%。这样得出的预测结果就是B。

软投票法与硬投票法可以得出完全不同的结论。相对于硬投票，软投票法考虑到了预测概率这一额外的信息，因此可以得出比硬投票法更加准确的预测结果。

当投票合集中使用的模型能预测出清晰的类别标签时，适合使用硬投票。当投票集合中使用的模型能预测类别的概率时，适合使用软投票。软投票同样可以用于那些本身并不预测类成员概率的模型，只要他们可以输出类似于概率的预测分数值（例如支持向量机、k-最近邻和决策树）。

通过以上的例子我们可以看出，不论是硬投票还是软投票，它对所有模型的处理是一样的，这意味着所有模型对预测的贡献是一样的。我们还可以调整每个不同分类器的权值，使其对整体模型的贡献度不同，来改良模型预测准确性。

4. 投票法的案例分析

Sklearn中提供了 VotingRegressor 与 VotingClassifier 两个投票方法。这两种模型的操作方式相同，并采用相同的参数。使用模型需要提供一个模型列表，列表中每个模型采用Tuple的结构表示，第一个元素代表名称，第二个元素代表模型，需要保证每个模型必须拥有唯一的名称。

例如，可以这样定义模型：

models = [('lr',LogisticRegression()),('svm',SVC()),('knn',KNeighborsClassifier(n_neighbors=1))]
ensemble = VotingClassifier(estimators=models)

有时某些模型需要一些预处理操作，我们可以为他们定义Pipeline完成模型预处理工作：

models = [('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC()))]
ensemble = VotingClassifier(estimators=models)

pipline的作用是，可以将多个处理步骤合并为单个Scikit-Learn估计器。而在本例中，就是将数据标准化之后，再进行svm操作。

该模型还提供了参数可以设置硬投票还是软投票（soft为软投票，hard为硬投票）：

models = [('lr',LogisticRegression()),('svm',SVC()),('knn',KNeighborsClassifier(n_neighbors=1))]
ensemble = VotingClassifier(estimators=models,voting='soft')

下面使用一个完整的例子演示投票法的使用：

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
from matplotlib import pyplot
from sklearn.datasets import make_classification

# 创建一个1000个样本，20个特征的随机数据集：
def get_dataset():
    X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2)
    # summarize the dataset
    return X,y

# 设置投票法模型，由以上VotingClassifier用法可知，其传入models参数为list()类型，这里设置一个由5个knn组成的硬投票方法，其中每个投票法的邻居值K参数不同
def get_voting():
    # define the base models
    models = list()
    models.append(('knn1', KNeighborsClassifier(n_neighbors=1)))
    models.append(('knn3', KNeighborsClassifier(n_neighbors=3)))
    models.append(('knn5', KNeighborsClassifier(n_neighbors=5)))
    models.append(('knn7', KNeighborsClassifier(n_neighbors=7)))
    models.append(('knn9', KNeighborsClassifier(n_neighbors=9)))
    # define the voting ensemble
    #硬投票方法
    ensemble = VotingClassifier(estimators=models, voting='hard')
    return ensemble

# 为了进行对比，这里是5个不同参数的knn和一个我们上面设置的投票法进行的对比。
# 还记得之前的超参数调优么，其实这个k就是个超参数，通过这种方法也可以选出最优的k。
def get_models():
    models = dict()
    models['knn1'] = KNeighborsClassifier(n_neighbors=1)
    models['knn3'] = KNeighborsClassifier(n_neighbors=3)
    models['knn5'] = KNeighborsClassifier(n_neighbors=5)
    models['knn7'] = KNeighborsClassifier(n_neighbors=7)
    models['knn9'] = KNeighborsClassifier(n_neighbors=9)
    models['hard_voting'] = get_voting()
    return models

# 用于对模型评分的方法，以分层10倍交叉验证三次重复的分数列表的形式返回。
from sklearn.model_selection import cross_val_score   #Added by ljq
def evaluate_model(model, X, y):
    #分层交叉验证
    cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
    scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
    return scores

# 最后展示结果
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
    scores = evaluate_model(model, X, y)
    results.append(scores)
    names.append(name)
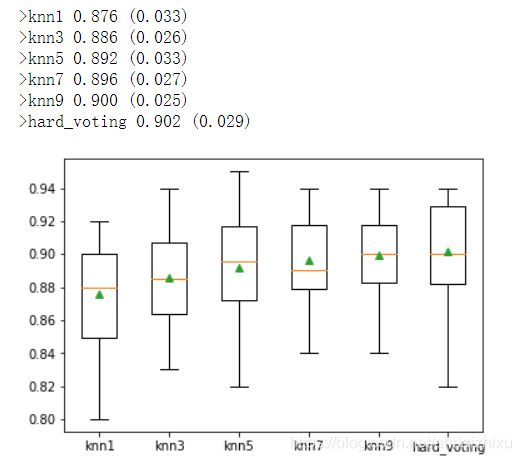
    print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))

#绘制箱型图
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

可以发现，投票法基本好于每一个基模型。