机器学习(三)——决策树(构建方法与分析泛化)
决策树
决策树学习是应用最广泛的归纳推理算法之一,学习一种逼近离散值目标函数的方法;树上每个节点指定了对实例的某个属性的测试,该节点的每一个后继分支对应于该属性的一个可能值;分类能力越强,越靠近根节点;任何属性在树的任意路径上最多仅出现一次。
优点:
1)对噪声有很好的健壮性且能够学习析取表达式;
2)可以表示为if-then的规则,逻辑性直观,可读性高,具有清晰的可解释性;
3)每一步都适用当前所有样例,大大降低了对个别样例错误的敏感性;
4)能处理不均一的数据,无需对数据进行标准量化,能够对缺少属性值的样例进行分类;
5)搜索假设完整空间,避免了搜索不完整空间的风险;
缺点:
- 只维护单一的当前分支假设;
- 搜索过程无回溯,属于爬山搜索,易得到局部最优而非全局最优
- 容易过拟合,需要在训练中设置限定条件或者训练后对树进行修剪
归纳偏置:优先选择最短的树(优选偏置)
核心问题:选取在每个节点要测试的属性
适用范围:
- 实例由“属性-值”对表示;2)目标函数具有离散的输出值;3)可能需要析取描述;4训练数据包含有错误;5)训练数据可以包含缺少属性值的实例
一、ID3算法:根据信息增益来衡量给定的属性区分训练样例的能力
![]()
算法步骤:
1)初始化属性集合和数据集合
2)计算数据集合和每一个候选属性信息熵,选择信息增益最大的属性作为当前决策节点
3)更新数据集合和属性集合(删除掉上一步中使用的根节点属性,将上一步选择的最佳节点作为根节点)
4)依次对当前根节点下的每种可能属性重复第二步
5)若子集只包含单一属性,则为叶子节点,根据其属性值标记。
6)完成所有属性集合的划分(所有属性都被包括;每个叶子节点属性值相同(熵为0))
特点:对可取值数目较多的属性有所偏好
二、C4.5算法:根据增益率衡量分类能力
增益率:增益率用信息增益Gain(S,A)和分裂信息度量SplitInformation(S,A)来共同定义:![]()
分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀):
![]()
特点:对可取值数目较少的属性有所偏好
三、基尼系数(CART决策树使用)
基尼系数衡量数据集纯度,值越小,数据纯度越高
四、决策树评价
假定样本的总类别为K个,对于决策树的某叶结点,假定该叶结点含有样本数目为n,其中第k类的样本数目为nk,k=1,2,...,K。
(1)若该结点中某类样本nj=n,而n1,...nj−1,nj+1,...nK=0,则该结点的熵Hp=0,最小;
(2)若该结点中各类样本数目n1=n2=...=nk=n/K,则该结点熵Hu=lnK,最大。
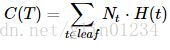
对所有叶结点的熵求和,该值越小说明对样本的分类越精确。各个叶结点包含的样本数目不同,可以使用样本数加权求熵和。因此,评价函数:
该评价函数值越小越好,所以,可以称为“损失函数”。
五、处理(降低复杂度,增加泛化能力)
1、过拟合问题
1)预剪枝(训练过程中设定)提早停止树增长
(1)每一个结点所包含的最小样本数,如10,则该结点总样本数小于10时,则不再分;
(2)指定树的高度或者深度,例如树的最大深度为4;
(3)指定结点的熵小于某个值,不再划分。
2)后剪枝(训练完成后,对已知决策树)
错误率降低修剪(减节点,替换成一个叶子节点,用最大分类属性替代);
规则后修剪(减规则前件,以最大提高决策精度)
