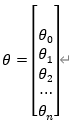机器学习之回归

近期阅读了《白话机器学习的数学》，为了将所读的内容充分理解消化，故将整理一系列文章，该篇是上一篇文章的续篇。

1.设置问题

基于广告费预测网站的点击量

2. 定义模型

1. 假设点击量只与广告费这一个变量有关，现有一些数据（广告费与对应点击量的值），在坐标系中表示为下图
   
   为了找出广告费与点击量之间的关系，可借助数学表达式即定义模型。为了方便，由上图建立广告费（x）与点击量（y)之间的函数关系为$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x$$即一次函数，这里的 $f_{\theta }$ 是指含有参数（变量）的函数，采用 ${\theta }_0$ 和 ${\theta }_1$ 代表变量，在机器学习中称为参数。一次函数的模型如下图：

机器学习中，变量或者预测值统称为参数。

3.如何求参

根据定义的模型求得的值与真实值存在一定的偏差，我们的目标就是使定义的模型求得的值尽可能贴近真实的值，也就是使模型的值与真实值的差值越来越小。

3.1 最小二乘法

最小二乘法就是不断修改参数的值，使得误差越来越小。

Q1：误差怎么表示？
A1：按照设定的模型，由已知数据来求 ${\theta }_0$ 和 ${\theta }_1$ 。由于 $f_{\theta }(x)$ 求得的值与实际值是有误差的，我们的目标就是将模型求得的值接近真实值，即使所有数据的误差和降到最小。误差表示为：$E(\theta )=\frac{1}{2}{\sum }_{i=1}^n(y^{(i)}-f_{\theta }(x^{(i)}){)}^2$ ，$E(\theta )$也称为目标函数，令其最小。其中$y^{(i)}和f_{\theta }(x^{(i)})$不是指y和f的i次幂，而是指第i个数据对应的实际的值和模型计算的值。

Q2：为什么$E(\theta )$是两者之差的平方而不是绝对值
A2：平方方便求微分（求导），而绝对值可能还需要对某些值的大小进行讨论

Q3：为什么需要乘$\frac{1}{2}$？
A3：结果导向，为了使最后的结果更加简单

为了求$E(\theta )$的最小值，对$E(\theta )$函数微分，以微分后的结果判断下一步 ${\theta }_0$和 ${\theta }_1$要调整的值，这里$x^{(i)}$和$y^{(i)}$为数据，值是已知的。

Q4：由微分结果如何调整参数的值？
A4：找到导数等于0的位置

最速下降法/梯度下降法

简单理解就是根据微分后的结果调整参数。
结合这个模型，$E(\theta )$含有两个参数${\theta }_0$和${\theta }_1$，这里就用到偏微分（偏微分是对含有多个变量的表达式微分的方法，当对某一个变量微分时，其他的变量视为常量）。
若直接使用$E(\theta )$对${\theta }_0$和${\theta }_1$偏微分，需要将$E(\theta )$的表达式展开，很复杂，这里使用复合函数求偏微分。以下为具体过程：
$$令u=E(\theta ),v=f_{\theta }(x)\frac{\vartheta u}{\vartheta \theta }=\frac{\vartheta u}{\vartheta v}\cdot \frac{\vartheta v}{\vartheta \theta }$$

因此

则${\theta }_0$的更新表达式为$${\theta }_0:={\theta }_0-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})$$
同理可求得${\theta }_1$的更新表达式为$${\theta }_1:={\theta }_1-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$$
其中 := 意为使用上一次的值更新下一次的值，$\eta$为学习率
学习率的确定需要不断尝试，若学习率太大，则会出现发散现象，可能在一个“谷底”荡来荡去无法收敛；学习率太小，则收敛速度则会很慢。
缺点：收敛速度慢，并且找的可能是“局部最优解”

3.2 多项式回归

将广告费与点击量之间的模型定义为$f_{\theta }(x)={\theta }_0+{\theta }_{1}x$，模型是线性的，也称为线性回归。对于数据散点图来说，曲线的模拟则会更贴合这些数据，方便起见，将模型定义为二次函数，如下图所示。

像这样，增加预测函数中多项式的次数的方法称为多项式回归。多项式回归能够对非线性的数据进行预测。

此时预测函数为：$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$$
当然这里也可以定义更高阶的函数，越高阶拟合效果越好，但可能会造成过拟合。
求参数的方法是一样的，也是对各个参数求偏导。
$${\theta }_0:={\theta }_0-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})$$
$${\theta }_1:={\theta }_1-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$$
$${\theta }_2:={\theta }_2-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})(x^{(i)}{)}^2$$

如果有${\theta }_3$、${\theta }_4$也是一样的方法。

3.3多重回归

目前为止讨论网站的点击量还是只与广告费这一个因素有关，实际上点击量是与多个因素相关的，也即存在多个变量。像这样包含了多个变量的回归称为多重回归。这里假设点击量与广告费$x_1$、广告栏的长度$x_2$和宽度$x_3$这三个变量有关

预测函数为$$f_{\theta }(x_1,x_2，x_3)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3$$
要求出参数${\theta }_0$、${\theta }_1$和${\theta }_2$的值，一样是对各个变量使用复合函数求偏导。

$${\theta }_0:={\theta }_0-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})$$
$${\theta }_1:={\theta }_1-\eta \sum _{i=1}^n(f_{\theta }(x_1^{(i)})-y^{(i)})x_1^{(i)}$$
$${\theta }_2:={\theta }_2-\eta \sum _{i=1}^n(f_{\theta }(x_2^{(i)})-y^{(i)})x_2^{(i)}$$
$${\theta }_3:={\theta }_3-\eta \sum _{i=1}^n(f_{\theta }(x_3^{(i)})-y^{(i)})x_3^{(i)}$$

为了一般化，假设这里有n个变量，则预测函数为：
$$f_{\theta }(x_1,x_2,...,x_n)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$$

求第 j 个的参数的表达式为
$${\theta }_j:={\theta }_j-\eta \sum _{i=1}^n(f_{\theta }(x_j^{(i)})-y^{(i)})x_j^{(i)}$$

为了简化预测函数，可以将参数和变量表示成列向量，如下：

为了便于运算和对齐，可添加$x_0=1$，如下

预测函数的表达式为$\theta$的转置与$x$的乘积，即$$f_{\theta }(x)={\theta }^{T}X$$

3.4随机阶梯下降法求参

最速下降法求参表达式为$${\theta }_j:={\theta }_j-\eta \sum _{i=1}^n(f_{\theta }(x_j^{(i)})-y^{(i)})x_j^{(i)}$$这里是使用了所有的$x,y$即数据，对于数据量巨大的情况，该方法的速度慢，计算量大；另外还可能找不到最优解或只找到局部最优解。
随机阶梯下降法是随机选择一个数据进行更新参数的值，则参数表达式为$${\theta }_j:={\theta }_j-\eta f_{\theta }(x_j^{(k)})-y^{(k)})x_j^{(k)}$$由于每次是随机选取一个数据进行更新参数的，因此不会陷入局部最优解，虽然有些难以置信，但该方法的结果确实会收敛。
此外，还可以选取一部分数据来求参，称为小批量梯度下降法。假设抽取k个数据，构成集合$K$。则求参表达式为$${\theta }_j:={\theta }_j-\eta \sum _{k\in K}(f_{\theta }(x_j^{(k)})-y^{(k)})x_j^{(k)}$$