三、Python数据挖掘（Numpy库）

三、Python数据挖掘（Numpy库）

---

一、Numpy 简介

• 什么是 Numpy？

Numpy 是一个开源的Python科学计算库，用于快速处理任意维度的数组

Numpy 支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy 比直接使用Python要简洁得多

Numpy 使用 ndarray 对象来处理多维数组，该对象是一个快速而灵活的大数据容器

• ndarray 的简介：

Numpy 提供了一个核心的数据结构——N维数组类型ndarray ，它描述了相同类型的 “items” 集合

• 什么要使用 ndarray 而不使用Python的原生 list？

ndarray与Python的原生 list 比较，其效率远远高于 list

机器学习与深度学习的最大特点就是大量的数据运算，那么如果没有一个快速的解决方案，那么可能现在Python也在机器学习领域也无法达到好的效果

Numpy 专门针对 ndarray 的操作和运算进行了设计，所以数组的存储效率和输入输出性能远优于Python中的嵌套列表，数组越大，Numpy 的这种优势就越发明显

ndarray 支持并行化运算（向量化运算），适合于机器学习

Numpy 底层使用C语言编写，内部解除了GIL（全局解释器锁），其对数组的操作速度不受Python解释器的限制，效率远高于纯Python代码；并且支持多线程

Numpy 中的函数与方法只能作用于 ndarray 对象（重要）

---

二、认识N维数组 ndarray 属性

ndarray 创建的数组中，要求其各元素的数据类型都是相同的，与Python的原生 list 不同，Python的原生 list 可以存储不同数据类型的数据（重要）

1.ndarray 属性

通过调用以下方法可以访问到属性值

属性名	含义
ndarray.shape	数组的维度形状，是一个元组
ndarray.ndim	数组维度数
ndarray.size	数组中的元素总数量
ndarray.itemsize	数组中一个元素的长度（字节）
ndarray.dtype	数组元素的类型

• 数组维度的元组，如：(6, 8) 指的是 6 行 8 列 的二维数组
• 在用 ndarray 创建数组的时候，如果没有指定类型，则 dtype 默认是整数 int64 或 浮点数 float64
• shape 和 dtype 是最重要的两种属性

导入模块：

import numpy as np

数组名 = np.array(N维数组)

使用ndarray创建一个N维数组

数组名 = np.array(N维数组, dtype=np.?)

指定数据类型地创建一个N维数组
dtype=np. 数据类型属性，如：dtype=np.int64，也可以使用简写 dtype=‘i8’，后面会详细介绍

2.ndarray 的形状 shape(tuple)

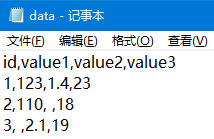
例：创建数组

import numpy as np

"""创建一个一维数组(3, )"""
list1 = np.array([1, 2, 3])
"""创建一个三维数组(2, 2, 3)"""
list2 = np.array([[[1, 2, 3], [4, 5, 6]], [[1, 2, 3], [4, 5, 6]]])

形状如图所示：

它们的 shape 属性分别是：(3, ) 和 (2, 2, 3)

维度的观察应该是从外到内，由大到小——得到形状 shape：

提示：由于 shape 是一个元组，因此可以用 shape 的下标来访问 shape 中的具体值，如：三维数组 temp 的元素个数为：sum = temp.shape[0] * temp.shape[1] * temp.shape[2]

3.ndarray 的类型 dtype

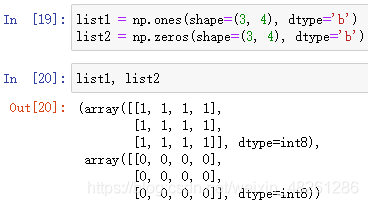
名称	含义	简写
np.bool	用一个字节存储的布尔类型(Ture或False)	‘b’
np.int8	一个字节大小，-128~127	‘i’
np.int16	整数，-32768~32767	‘i2’
np.int32	整数，-231~231-1	‘i4’
np.int64	整数，-263~263-1	‘i8’
np.unit8	无符号整数，0~255	‘u’
np.unit16	无符号整数，0~65535	‘u2’
np.unit32	无符号整数，0~232-1	‘u4’
np.unit64	无符号整数，0~264-1	‘u8’
np.float16	半精度浮点数，16位，正负号1位，整数5位，精度10位	‘f2’
np.float32	单精度浮点数，32位，正负号1位，整数8位，精度23位	‘f4’
np.float64	双精度浮点数，64位，正负号1位，整数11位，精度52位	‘f8’
np.complex64	复数，分别用两个32位浮点数表示实部和虚部	‘c8’
np.complex128	复数，分别用两个64位浮点数表示实部和虚部	‘c16’
np.object_	Python对象	‘O’
np.string_	字符串	‘S’
np.unicode_	unicode类型	‘U’

在通过 dtype=np.? 指定数据类型时，可以使用名称或简写

---

三、基本操作

1.生成数组的方法

（1）生成0和1的数组：

数组名 = np.zeros(shape=?, dtype=?)

生成元素均为0的数组
shape 指定数组的形状

数组名 = np.ones(shape, dtype=?)

生成元素均为1的数组
shape 指定数组的形状

例：指定为 py.int8 类型

（2）从现有数组中生成：

新数组 = np.array(旧数组)

深拷贝旧数组

新数组 = np.copy(旧数组)

深拷贝旧数组

数组名 = np.asarray(旧数组)

浅拷贝旧数组

数组名.flatten()

将多维数组拍扁成一维数组，顺序不变，并返回新的数组
注：只返回新数组，不改变原数组

• 一般可以将 Python 的数组转化为 Numpy 的数组
• 深拷贝：拷贝成新的数组，和旧数组没有关联
• 浅拷贝：引用旧数组的引用，当旧数组发生变化时，它也跟着发生变化

（3）生成固定范围的有序数组：

np.linspace(start, stop, num, endpoint, retstep, dtype)

在 [start, stop] 之间生成元素值等间距的数组，元素个数为sum 个
start 数组的起始值，该值包含在内
stop 数组的终止值，该值包含在内
num 要生成的等间距的元素个数，默认为50个（如果 endpoint=True，则该值必须指定）
endpoint 数组中是否包含 stop 值，默认为 True
retstep 如果为True，则返回样例，以及连续数字之间的步长
dtype 输出 ndarray 的数据类型

np.arange([start, ]stop[, step])

在 [start, stop) 之间，用法和Python中的 range() 一样

例：

（4）生成随机数组：

生成随机数组，包括两种分布状况：均匀分布 和 正态分布

需要使用 np.random 模块

均匀分布：

np.random.rand(d0, d1,…,dn)

从 [0.0, 1.0) 之间生成一个均匀分布的随机数数组，d0~dn可以指定其数组形状，如：np.random.rand(2, 3)，生成 shape=(2, 3) 的二维数组
rand() 即没有指定形状，返回一个浮点数

np.random.uniform(low=0.0, high=1.0, size=None)

从 [low, high) 之间生成一个均匀分布的随机数数组
low 采样下界，float 类型，默认值为0.0
high 采样上界，float 类型，默认值为1.0
size 输出样本数目，为 int 或 shape ，例如：size=(m, n, k)，则生成 shape=(m, n, k) 的数组，缺省时生成一个元素

例：np.random.rand(…)
np.random.rand() 返回一个浮点数
np.random.rand(1) 返回一个包含1个元素的一维数组
np.random.rand(2) 返回一个包含2个元素的一维数组
np.random.rand(5, 8) 返回一个包含5 × 8 = 40个元素的二维数组

例：np.random.rand(…) 的均匀度验证

import numpy as np
import matplotlib.pyplot as plt

temp_list = np.random.rand(1000000)

"""绘图"""
plt.figure(figsize=(5, 5), dpi=100)
plt.hist(temp_list, 100)
plt.show()

例：np.random.uniform(…) 的均匀度验证

import matplotlib.pyplot as plt

temp_list = np.random.uniform(low=0.0, high=1.0, size=1000000)

plt.figure(figsize=(5, 5), dpi=100)
plt.hist(temp_list, 100)
plt.show()

正态分布：

正态分布是一种概率分布，它是具有有两个参数 μ 和 σ 的连续型随机变量的分布，其中 μ 是服从正太分布的随机变量的均值；σ² 是此随机变量的方差，所以正态分布记作 x~N (μ, σ²)

简单来说， μ 决定了正态分布图 对称轴的位置/最大值点；而 σ 则决定了正态分布图的 粗细程度 和 最大值

• 当 σ² 越小时，正态分布图越细高，最大值也越大
• 当 σ² 越大时，正态分布图越粗扁，最大值也越小

此外，x~N (0, 1) 被称为标注正态分布

np.random.randn(d0, d1,…,dn)

从标准正态分布中生成一个数组，d0~dn可以指定其数组形状，如：np.random.randn(2, 3)，生成 shape=(2, 3) 的二维数组
randn() 即没有指定形状，返回一个浮点数

np.random.normal(loc=0.0, scale=1.0, size=None)

以正态分布的概率生成一个数组
loc 概率分布的均值 μ，float 类型，默认值为0.0
scale 概率分布的标准差 σ，float 类型，默认值为1.0
size 输出样本数目，为 int 或 shape ，例如：size=(m, n, k)，则生成 shape=(m, n, k) 的数组，缺省时生成一个元素

例：np.random.randn(…) 与 np.random.normal(…) 的正态分布验证

import numpy as np
import matplotlib.pyplot as plt

temp_list = np.random.randn(1000000)

plt.figure(figsize=(5, 5), dpi=100)
plt.hist(list1, 1000)
plt.show()

import numpy as np
import matplotlib.pyplot as plt

temp_list = np.random.normal(loc=0.0, scale=1.0, size=1000000)

plt.figure(figsize=(5, 5), dpi=100)
plt.hist(list1, 1000)
plt.show()

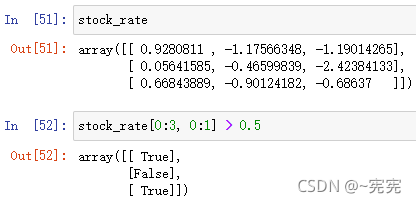
2.数组的索引和切片

索引数组中的某一元素：

数组名[d0, d1,…,dn]
访问数组的某一元素
d0, d1,…,dn 按形状分布的下标选取即可

切片/访问一维数组中某一范围的元素：

数组名[start:stop]

切片/访问—→行下标在 [start, stop) 区间内的数组元素，返回一个数组

切片/访问二维数组中某一范围的元素：

数组名[row, [start:stop]]

切片/访问二维数组 中—→行下标为 row ，列下标在 [start, stop) 区间内的数组元素，返回一个数组
当 start:stop 缺省时，表示访问—→行下标为 row 的行
row 也可以写成 start:stop 的形式，表示行下标在 [start, stop) 区间的范围内

切片/访问三维数组中某一范围的元素：

数组名[axis[, row][, start:stop]]

切片/访问三维数组中—→轴下标为 axis，行下标为 row，列下标在下标在 [start, stop) 区间内的数组元素，返回一个数组
当 row, start:stop 缺省时，表示访问—→轴下标为 axis 的平面
当 start:stop 缺省时，表示访问—→轴下标为 axis，行下标为 row的行
axis 也可以写成 start:stop 的形式，表示轴下标在 [start, stop) 区间的范围内
row 也可以写成 start:stop 的形式，表示行下标在 [start, stop) 区间的范围内

• start 均可以缺省，默认值为0
• stop 也可以缺省，默认访问到数组最后

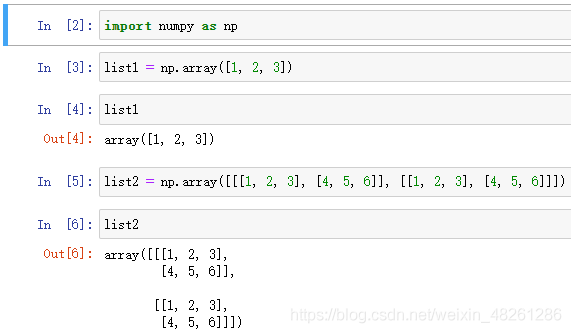
例：

此外，axis 或 row 也可以用 start:stop 代替：

如：数组名[0:2, 0:5] 表示数组的第0~1行中的第0~4列的元素

3.数组形状的修改

数组对象调用方法：

数组名.reshape(shape)

把当前数组返回为 shape 的形状，元素的所有顺序 [start, stop) 并不发生改变
注：只返回新数组，不改变原数组

数组名.resize(shape)

直接对当前数组进行修改，改变原数组，没有返回值，元素的所有顺序 [start, stop) 并不发生改变

数组名.T

返回一个 转置 后的二维数组，把行变为列，把列变为行，元素的所有顺序 [start, stop) 发生了改变
注：只返回新数组，不改变原数组

例：数组名.reshape(shape)

例：使用 数组名.reshape(shape) 时，如果只想指定列数不想计算行数可以用 -1 代替

例：数组名.T

3.数组数据类型的修改

数组名.astype(dtype)

将当前数组的数据类型转化为 dtype，并返回
注：只返回新数组，不改变原数组

数组名.tobytes()

把数组转化成二进制的 bytes 类型存储并返回，序列化到本地时使用
注：只返回新数组，不改变原数组

• 如果遇到 IOPub data rate exceeded 错误，原因是：
  在 Jupyter Notebook 中对输出的字节数有限制，可以修改配置文件
  不过这个错误仅仅影响显示出来的内容数，对函数的功能没有影响，不必理会

4.数组的去重

np.unique(数组)

将数组拍扁为一维数组（即可以作用于多维数组），并进行去重，返回新数组
注：只返回新数组，不改变原数组

例：

---

四、ndarray 运算

1.逻辑运算

直接使用数组名的逻辑表达式 ⇨ 返回值：布尔数组

布尔逻辑表达式 ⇨ 返回值： 布尔数组
进行基本的逻辑运算，该表达式记为“布尔数组”（重要）
布尔数组：由 True 或 False 组成的数组

例：

例：

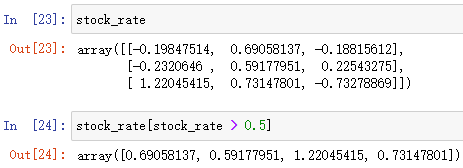
数组名[布尔数组]

布尔索引，索引布尔数组中为 True 的元素，并返回这些元素组成的数组
下标访问数组的一种办法——布尔索引

数组名[布尔数组] = 新的值

将布尔数组中为 True 的元素进行统一的赋值为新的值，并返回新数组（基于布尔数组中的旧数组）

例：

例：

• 其他逻辑运算符均适用

通用判断函数：

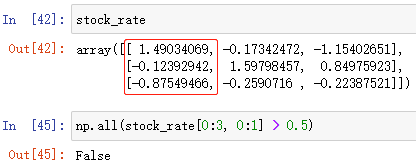
np.all(布尔数组)

布尔数组中只要有一个 False 就返回 False

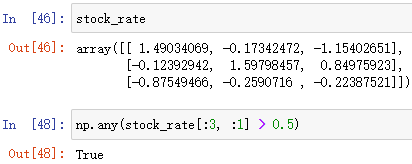
np.any(布尔数组)

布尔数组中只要有一个 True 就返回 True

例：np.all(布尔数组)

例：np.any(布尔数组)

三元运算符：

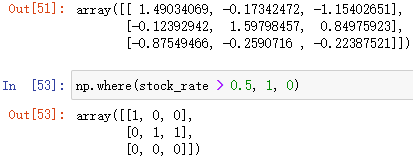
np.where(布尔数组, data1, data2)

判断布尔数组中的内容，True 的元素全部赋值为 data1，False 的元素全部赋值为 data2，，并返回新数组（基于布尔数组中的旧数组）

例：

想要进行更复杂的运算，需要使用布尔逻辑运算函数：

布尔逻辑运算函数	含义
np.logical_and(布尔数组1, 布尔数组2)	逻辑与
np.logical_or(布尔数组1, 布尔数组2)	逻辑或
np.logical_not(布尔数组1, 布尔数组2)	逻辑非
np.logical_xor(布尔数组1, 布尔数组2)	逻辑异或

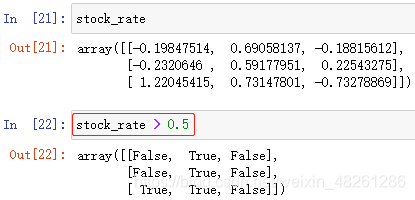
例：把数组中 > 0.5 或 < -0.5 的元素置1，否则置0

2.统计运算

在数据挖掘/机器学习领域，统计指标的值也是我们分析问题的一种方式，常用的有：最大值max、最小值min、平均值mean、中位数median、方差var、标准差std 等

统计相关函数：

统计运算函数	含义
np.max(数组[, axis=])	找到数组中最大值元素
np.min(数组[, axis=])	找到数组中最小值元素
np.mean(数组[, axis=])	统计数组的平均值
np.median(数组[, axis=])	找到数组的中位数
np.var(数组[, axis=])	统计数组的方差
np.std(数组[, axis=])	统计数组的标准差

• axis 指定按行或按列运算：
  axis=0 表示按列统计，即分别统计每一列中的 ( max 或 min 或 mean…)
  axis=1或-1 表示按行统计，即分别统计每一行中的 ( max 或 min 或 mean…)

例：按行统计最大值

寻找最大值、最小值所在位置：

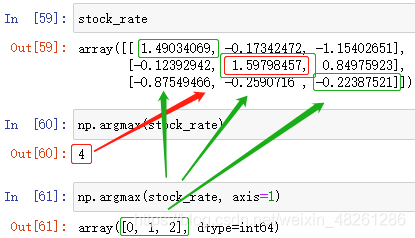
np.argmax(数组[, axis=])

找到数组中最大值元素，返回其所在位置——下标

np.argmin(数组[, axis=])

找到数组中最小值元素，返回其所在位置——下标

• axis 指定按行或按列运算：
  axis=0 表示按列统计，即分别统计每一列中的 ( max 或 min 或 mean…)
  axis=1或-1 表示按行统计，即分别统计每一行中的 ( max 或 min 或 mean…)
• 当有多个最大值或最小值时，返回首个查找到的最大值/最小值的下标值

例：寻找最大值的位置，分别用 总体 和 按行

3.数组间的运算

注：Python的原生 list 是没有这些功能的

数组与数之间的运算：

例：

例：

数组与数组之间的运算：

广播机制 broadcast

若想要让两不同形状的数组之间能够进行运算，它们需要满足广播机制

解析——推导（重点）：

我们发现，不同的数组之间的运算，不论它们是不是同维数组，只要它们的 shape 中同一列所对应的值是相等的，那么它们之间就能够一一对应，那么它们之间就是可运算的

此外，除了 shape 同一列的一一对应之外，我们发现，若 shape 的某一列中其中一个是1，那么这个1就可以对应另一个数组在该列上的所有元素，称为一对多，那么这种一对多的对应也是可以运算的

广播机制：

当操作两个数组时，numpy会逐个比较它们的 shape（构成的元组 tuple），只有在 shape 中每一列对应的数 满足下述所有条件下，两个数组之间才能进行数组与数组的运算：

• 任一列上的两数相等，即满足 “一一对应”
• 任一列上的两数中，其中一个数是1，即满足 “一对多”

那么两数组之间就是可运算的，满足广播机制后，那么数组之间的运算就是简单的——对应的元素通过运算符号进行运算即可 (+、-、*、/)

例：
A (256, 256, 3)
B (3, )
在 col(d2) 列上，满足3对应3，因此A、B之间是可运算的

A (9, 1, 7, 1)
B (8, 1, 5)
在 axis(d1) 列上，满足1对8；在 row(d2) 列上，满足1对7；在 col(d3) 列上，满足1对5，因此A、B之间是可运算的

A (5, 4)
B (1, )
在 col 列上，满足1对4，因此A、B之间是可运算的

A (15, 3, 5)
B (15, 1, 1)
在 axis(d0) 列上，满足15对应15；在 row(d1) 列上，满足1对3；在 col(d2) 列上，满足1对5，因此A、B之间是可运算的

A (10, )
B(12, )
在 col 列上，10和12无法对应，显然A、B之间不可运算

A (2, 1)
B (8, 4, 3)
虽然在 col(d1) 列上，满足1对3；但是在 row(d0) 列上，2和4无法对应，显然A、B之间不可运算

例：数组与数组之间的运算

显然，运算结果为new_array = [[1 * 10, 2 * 20], [3 * 10, 4 * 20]]

4.矩阵运算

存储矩阵的两种方式：

矩阵名 = np.array()

ndarray 存储矩阵

矩阵名 = np.mat()

matrix 存储矩阵

矩阵 matrix 是 《线性代数》 中的概念，它必须是2维的，矩阵之间的 乘运算 的几何意义是 坐标系或向量的线性变换 ，详见

• 线性代数的本质——动画+描述（向量、矩阵、线性变换和矩阵乘法）

其运算方法为：

np.matmul(a, b, out=None)

两个numpy矩阵相乘

np.dot(a, b)

可用于两个numpy矩阵相乘，也可以用于矩阵与标量（常量）相乘

例：按照平时成绩 0.4 和期末成绩 0.6 的加权值来计算出最终成绩

最终成绩为 (8, 1) 的矩阵，而学生成绩是 (8, 2) 的矩阵，因此，权值应该写成 (2, 1) 的矩阵，即：

• (8, 2) × (2, 1) = (8, 1)

数据：
grade = np.array([[80, 86], [82, 80], [85, 78], [90, 90], [86, 82], [82, 90], [78, 80], [92, 94]])

import numpy as np

grade = np.array([[80, 86], 
                  [82, 80], 
                  [85, 78], 
                  [90, 90], 
                  [86, 82], 
                  [82, 90], 
                  [78, 80], 
                  [92, 94]])
weighting = np.array([[0.4], [0.6]])

np.matmul(grade, weighting)

扩展：

matrix1 * matrix1

用 matrix 存储的两个矩阵可以直接用 * 相乘

ndarray1 @ ndarray2

用 ndarray 存储的两个矩阵可以用 @ 相乘
注：如果两 ndarray 使用 * 来进行运算， ndarray 将被视作数组，数组之间的运算需要满足广播机制

5.np.matmul() 与 np.dot() 的区别

• 二者都是矩阵乘法
• np.matmul() 不允许矩阵与标量（常量）相乘
• 在矢量与矢量的内积运算中，np.dot() 与 np.matmul() 没有区别
• 在 np.matmul() 中，可以传入N(N>2)维的数组

在 np.matmul() 传入N(N>2)维的数组时，它会作如下的处理：

• 首先会把N(N>2)维数组的最后两个维度作为矩阵堆栈——即把数组的 shape (d0, d1, d2, … , dn) 的 (dn-1, dn) 视为完整的矩阵——矩阵堆栈，然后再对两者之间的矩阵进行 “一一对应” 或者 “一对多”（详见广播机制） 的矩阵相乘运算，因此N(N>2)维的数组需要满足广播机制
• 简单来说，它是把N(N>2)维数组中的 shape (d0, d1, d2, … , dn) 中的 dn-1 和 dn 视为 d′（一个矩阵），于是这个N(N>2)维数组变为 shape (d0, d1, d2, … , dn-2, d′)，因此这个数组要想跟另一个数组进行运算，就需要满足数组运算之间的广播机制，在满足广播机制之后，两个数组的 矩阵d′ 之间就可以进行 “一一对应” 或者 “一对多” 的运算

例：

import numpy as np

a = np.arange(2 * 2 * 4).reshape((2, 2, 4))
b = np.arange(2 * 2 * 4).reshape((2, 4, 2))
c = np.arange(1 * 2 * 4).reshape((1, 4, 2))
np.matmul(a, b)
np.matmul(a, c)

首先讨论 np.matmul(a, b)：

对于矩阵 a，它在 np.matmul() 中会被理解成 两个 2×4 的矩阵
对于矩阵 b，它在 np.matmul() 中会被理解成 两个 4×2 的矩阵

因此运算结果为 out[ ] ：

其次是 np.matmul(a, c)：

因此运算结果为 out[ ] ：

6.合并与分割

数组水平合并/拼接：

np.hstack(*args)

对数组元组 *args 中的数组进行 水平 方向上的合并
*args 数组元组，如：(ndarray1, ndarray2, … , ndarrayn)

例：

例：

数组竖直合并/拼接：

np.vstack(*args)

对数组元组 *args 中的数组进行 竖直 方向上的合并
*args 数组元组，如：(ndarray1, ndarray2, … , ndarrayn)

例：

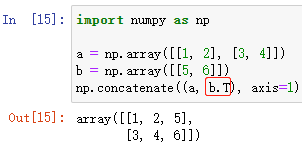
np.concatenate(*args, axis=)

对数组元组 *args 中的数组进行 水平或竖直 方向上的合并
*args 数组元组，如：(ndarray1, ndarray2, … , ndarrayn)
**kwargs 中，axis=? 可以指定进行 水平或竖直 的拼接

• axis 指定按行或按列进行拼接：
  axis=0 表示进行竖直拼接（列方向）
  axis=1或-1 表示进行水平拼接（行方向）

例：（注：这里的 数组b 进行了 T 转置）

例：将第一行和第三行的数据进行水平拼接

数据：
stock_rate = [[1.18713375, 0.77624391, -0.47452542], [-1.22011298, 1.26038645, 0.10170957], [-0.67131837, 1.47798017, -0.69569189]]

数组分割：

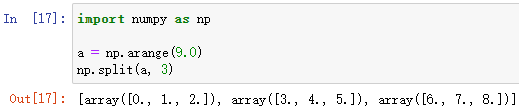
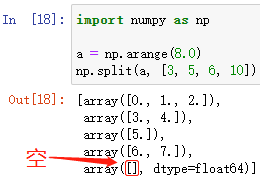
np.split(ndarray, indices_or_sections, axis=0)

对数组进行指定份数的分割
ndarray 为需要分割的数组
indices_or_sections 为指定的分割参数，可以是：

• 整数——平均分成整数份，如：3，即把 ndarray 平均分成3分
• 整数数组——以数组中的整数元素作为索引，索引对应 ndarray 中的元素作为分隔，如：[1, 2, 3]，即把 ndarray 中下标为1、2、3的元素作为分隔，其中，分隔元素将作为下一个数组的首元素

例：

例：

7.IO操作与数据处理

Numpy 读取数据文件：

np.genfromtxt(fname, delimiter=?)

把数据文件读取到 ndarray 数组中
fname 文件路径和文件名，文件名包含扩展名
delimiter=? 分隔符，用于区分不同元素，不会将分隔符读入数组

• 分隔符区分一维数组的不同元素，不同的行则为二维数组中的不同列

例：

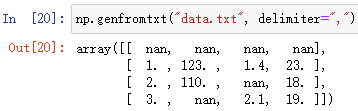
发现，对于字符串数据和空格数据都会读取成 缺失值nan（dtype 为 float64）

如何处理缺失值？

思路1：

直接删除含有缺失值的样本

思路2：

替换/插补——按列求平均值，用平均值来填补 缺失值nan

例：替换/插补 nan 的函数定义

import numpy as np


def fill_nan_by_column_mean(t):
    for i in range(t.shape[1]):
        # 获取nan的个数
        nan_num = np.count_nonzero(t[:, i][t[:, i] != t[:, i]])
        if nan_num > 0:
            # 获取当前列的元素
            now_col = t[:, i]
            # 求和
            now_col_not_nan = now_col[np.isnan(now_col) == False].sum()
            # 和/个数
            now_col_mean = now_col_not_nan / (t.shape[0] - nan_num)
            # 赋值给now_col
            now_col[np.isnan(now_col)] = now_col_mean
            # 赋值给t，即更新t的当前列
            t[:, i] = now_col

    return t

• 比较复杂，以后我们将会介绍 Pandas 库来处理这些数据

上述所用函数：

np.count_nonzero(ndarray, axis=None, *, keepdims=False)

用于统计数组中非零元素的个数
ndarray 被统计的数组
axis=None 指定是否按轴统计，指定后则按行/列分别进行非零元素的统计
keepdims 未知…

np.isnan(ndarray)

逐个检查 ndarray 中的值是否为 nan，并以布尔数组的形式返回

• axis 指定按行或按列运算：
  axis=0 表示进行水平拼接
  axis=1或-1 表示进行竖直拼接

例：

8.扩展：axis=0或1 的交互方式

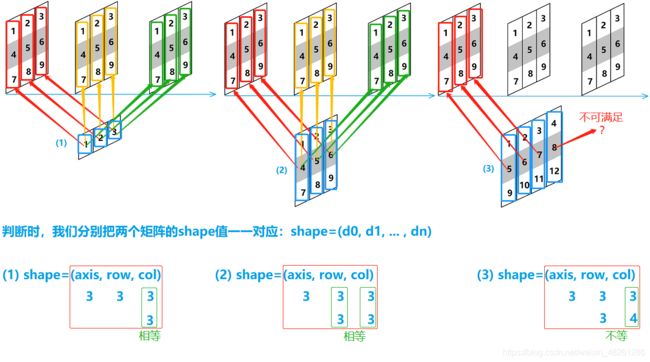
在很多函数中，我们多使用到了 axis=0或1 的参数，但我们只是针对二维数组来进行简要说明，在这里，我们将对 axis=0或1 的用法进行 N(N>2)维数组 的展开：

在传递 axis=0或1 参数的函数中，我们需要明确一点：

• 假设这个 N(N>2)维数组 的形状为：shape (d0, d1, d2, …, dn)

那么首先要对 N(N>2)维数组 进行降维度，它会把 shape (d0, d1, d2, …, dn) 的 N(N>2)维数组 先拆分成 d0 个 N-1(N>2)维数组，这个时候 axis=0或1 就很好解读了：

• 对于拆分后的 d0 个 N-1(N>2)维数组，有以下规则：
• 当 axis=1 时：d0 个 N-1(N>2)维数组，每个数组都在自身内部进行统计，和其他数组没有关联
• 当 axis=0 时： d0 个 N-1(N>2)维数组，这些数组将会被一一串起来（每个数组的形状是一样的），因此 d0 个数组 之间，每个数组之间的数都是一一串联对应的，如图：
  
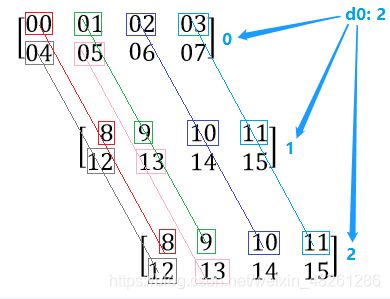
  于是， axis=0 就表示每个数组将会与其他数组之间进行统计，每串数数进行对应统计

例：三维数组

内部按列统计：

外部统计：

例：四维数组

内部统计：

外部统计：