【吴恩达机器学习 - 1】利用梯度下降算法与正规方程实现线性回归及多元线性回归（课程练习第一题ex1）

前言先来几句废话，相信大部分都是在B站看的吴恩达的机器学习视频，寻思着做做练习才有缘在这个页面见面，建议到吴恩达的课程网站https://www.coursera.org/，注册个账号，那就可以直接利用里面的资料了，包括每次的练习文件，数据集，提交对错检验等，若觉得有点麻烦，我也会把该节练习的相关资料的云盘扔到评论区，自行下载

对了还有一点，为了与吴恩达的课程相匹配，该系列的相关内容均使用Octave进行演示，话不多说，下面开始正文

1. 热身

练习中的第一个部分，是一个简单的小热身，打开warmUpExercise.m文件中，你会发现如下代码，只需要把需要补充的部分写到指定位置即可

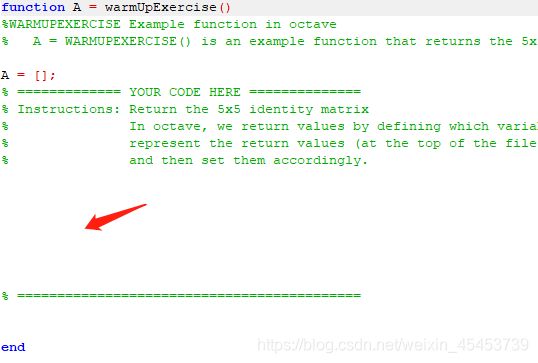
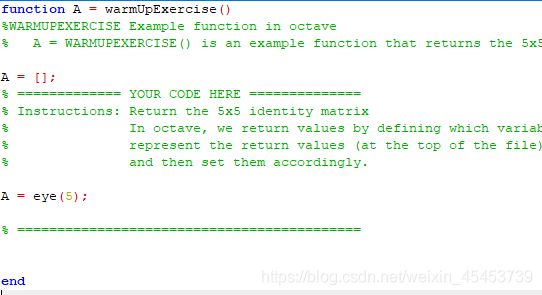
该节练习的需求为定义一个5*5的单位矩阵，其实文件中也有提示，代码很简单，写完后别忘记保存

A = eye(5);

运行一下ex1.m文件即可查看是否成功（在命令窗口输入ex1回车即可）

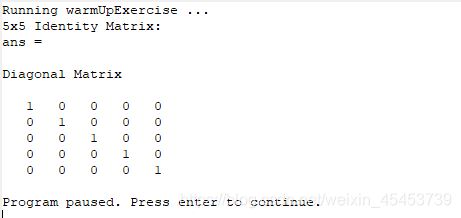
ok，小热身已经搞定了（若已经注册课程账号的同学也可以执行submit.m文件进行提交操作即可查看结果是否正确）

2. 线性回归

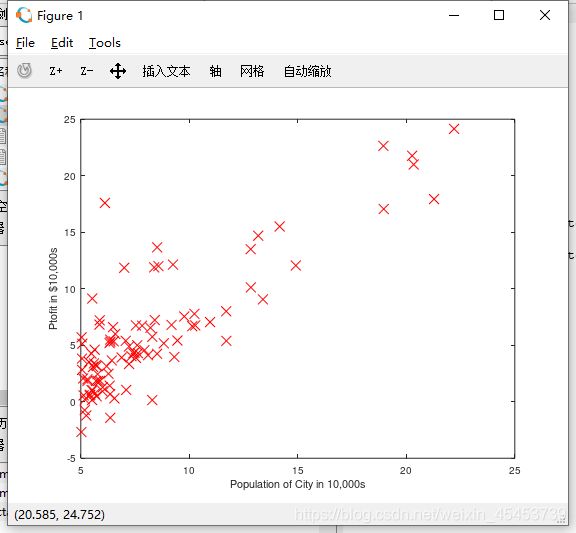
2.1 绘制数据图

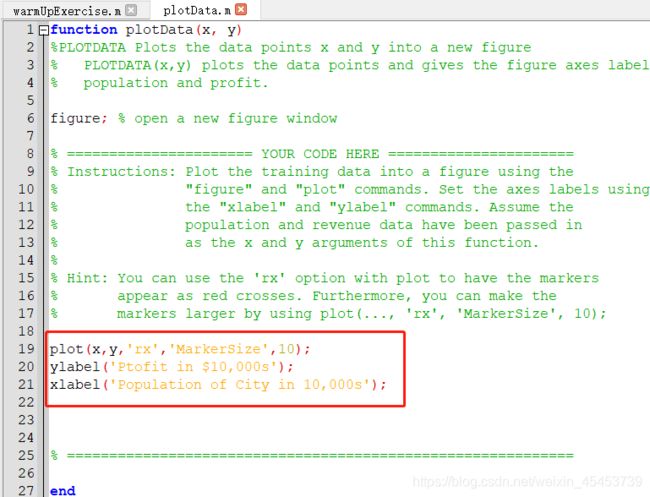
该部分的所需要完善的文件是plotData.m，同样的，文件中也有提示该输入的代码，我们只需要跟着操作就好了

plot(x,y,'rx','MarkerSize',10);
ylabel('Ptofit in $10,000s');
xlabel('Population of City in 10,000s');

这时候再次运行ex1.m，在卡住后按下回车便能看到该数据集的绘图

2.2 完善梯度下降算法

这部分就是重头戏了，还记得在课程中所介绍到的梯度下降算法吗？

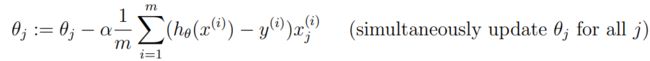
我们的工作就是把这条公式转化成对应的语句写到gradientDescent.m文件中，该部分的练习是只有单个特征值，因此对应的线性方程只有两个参数，那么我们就只写这两个参数的迭代更新方程（注意是需要同步更新所有变量，所以需要利用辅助变量）

temp1 = theta(1) - alpha * sum(X*theta-y)/m;
temp2 = theta(2) - alpha * sum((X*theta-y).*X(:,2))/m;
theta(1) = temp1;
theta(2) = temp2;

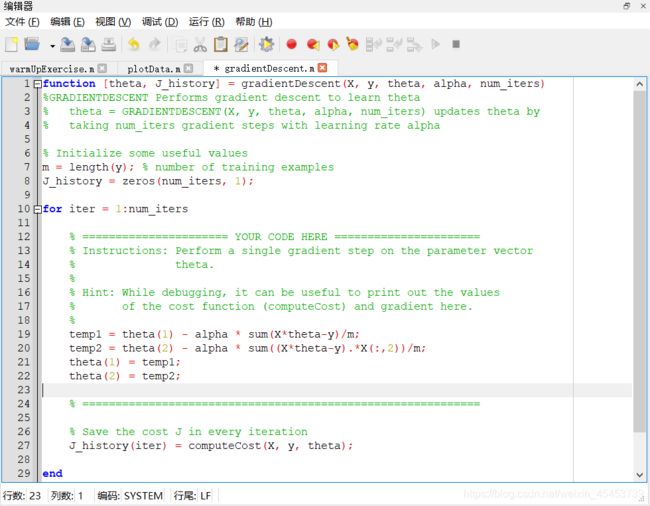
这时候你发现该函数中还有一个计算代价函数的函数，因此需要打开computeCost.m文件，完善其代价函数计算算法，什么？忘了啥是代价函数？来来来

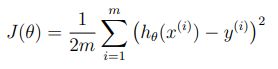
接下来就该把这个函数转化成如下代码啦

J = sum((X * theta - y).^2)/2/m;

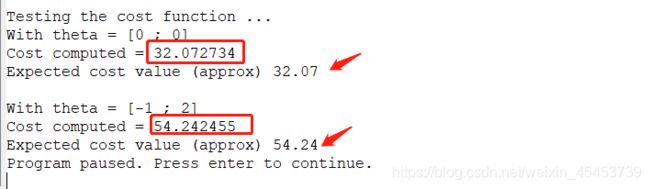
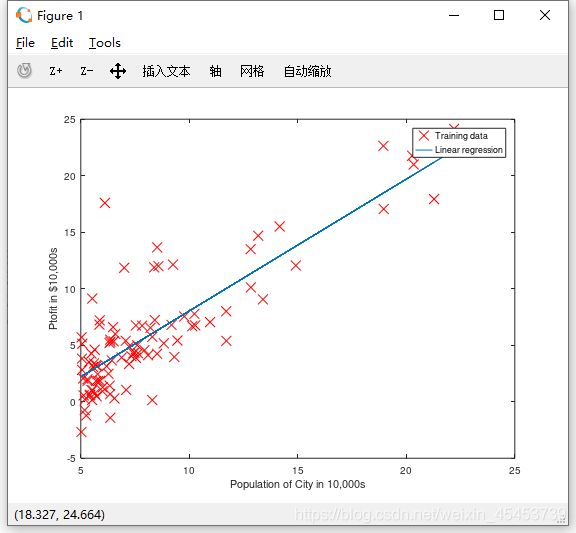
这时候，你可以运行一下ex1.m文件，查看你所书写的算法所得出的结果与标准结果是否相同

再次按下回车，你还可以查看最终得出的参数结果

还可以在数据图像中看到最终的预测线性方程

当然，最后你还可以看到人口值为35000与70000时候的利润预测值

2.3 可视化代价函数

该部分不需要我们来完成，资料中已经写好相关的代码，我们只需要看一下感受一下代价函数的图形是怎么样的即可（在右侧等高图中的小红X表示的时最终迭代得到的参数所对应代价函数的位置）

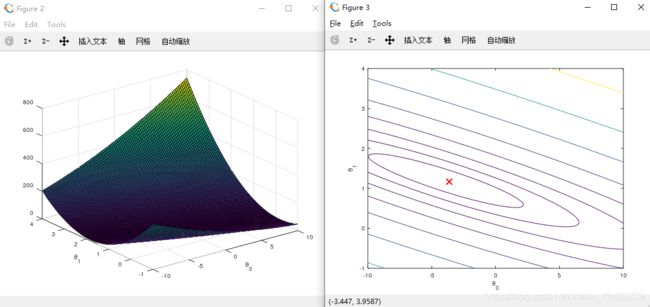
到这里，你已经完整地实现了利用梯度下降算法进行单特征值的线性回归，但生活中很多情况，都是很多个特征是才能决定最终结果，因此我们来做一下延伸练习

3. 多元线性回归

3.1 梯度下降法（Gradient descent）

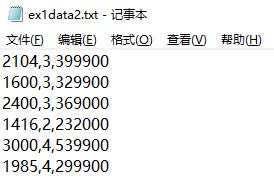
我们先来看一下这个数据集，发现数据集的特征值之间的范围相差非常大，这造成的结果就是迭代的速度非常慢

因此第一步我们需要进行特征缩放

3.1.1 特征缩放（Feature normalization）

我们需要完善featureNormalize.m文件以实现特征缩放，特征缩放有多重方法，吴恩达老师再上课时所介绍的特征缩放是利用均值归一化

而在本作业中则是建议使用标准化进行

其实两种方法都可以使用，但为了后续的内容讲解，这里选择使用标准化进行特征缩放较为简便

mu = mean(X);                 #取均值
sigma = std(X);               #标准化
X_norm = (X.-mu)./sigma;

3.1.2 梯度下降

同样的，在该部分练习中我们也需要进行梯度下降算法与代价函数的完善，因考虑到该练习为多特征值，因此随后算法的部分内容也转换为矩阵运算进行

• 梯度下降

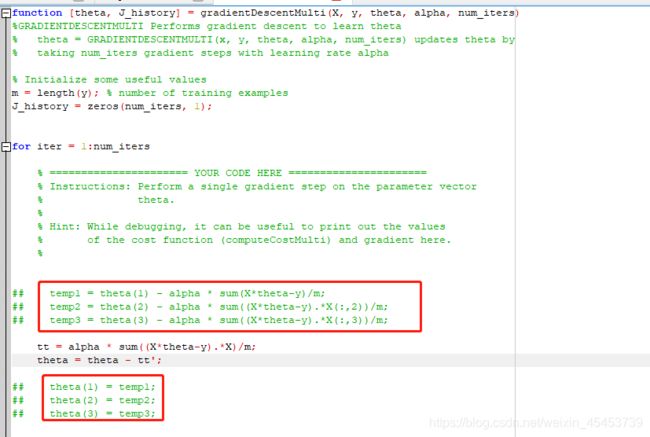
在gradientDescentMulti.m文件中

tt = alpha * sum((X*theta-y).*X)/m;
theta = theta - tt';

红框中的算法为不采用矩阵运算的算法，较为复杂麻烦，仅供参考

• 代价函数

在computeCostMulti.m文件中

J = sum((X*theta-y).^2)/2/m;

这里的代价函数算法其实与第二节中一致，因为在第二节的算法中我已经是运用矩阵运算进行

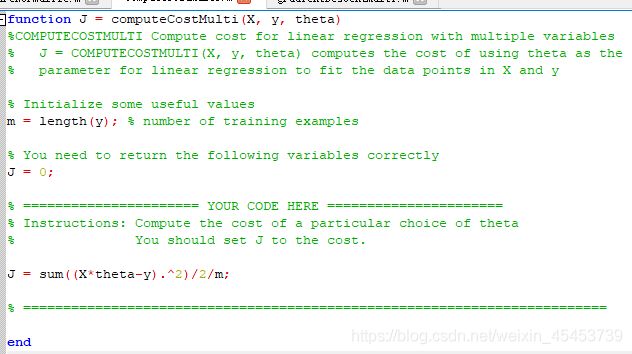
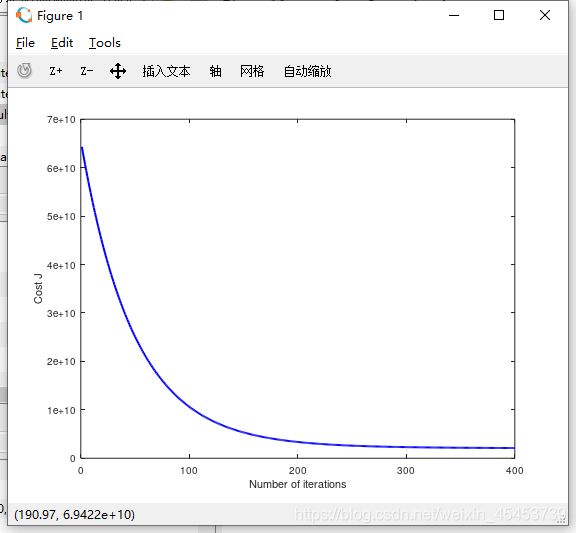
到此，多元线性回归梯度下降算法也已经完成了，这时候运行ex1_multi.m文件即可看到迭代次数与代价函数间的规律曲线

3.1.3 放假预测

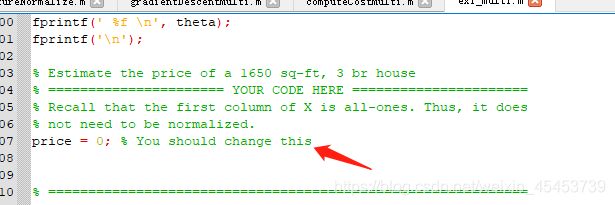
细心的你突然发现，怎么这里的房价预测值为0？这是怎么回事呢？

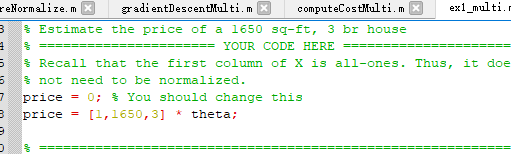
再细心查看一下主程序ex1_multi.m你会发现，这价格计算根本还没有写（其实这是一个考点）

不管三七二十一，你把该价格计算写上了

price = [1,1650,3] * theta;

咦？可是好像不对？怎么可能预测房价这么高呢？

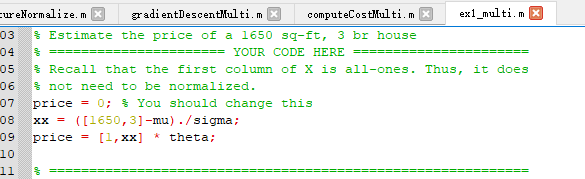
恭喜你，掉坑了，还记得刚刚训练时候运用到了特征缩放吗？换言之，该训练的参数是对进行特征缩放后的特征值才有用，因此在计算预测房价前，我们需要对其进行特征缩放后再进行计算

xx = ([1650,3]-mu)./sigma;
price = [1,xx] * theta;

最终得到的房价预测值，显然就可以认为得到合适的答案

至此，你也已经实现了多元线性回归并且得到正确的结果了，但是觉不觉得这种情况下利用梯度下降进行有点麻烦？有没有更简单的方法呢？有的，下面来用正规方程解决这个问题

3.2 正规方程（Normal equation）

正规方程也是吴恩达老师在上课时候介绍的一个方法，什么？又忘了是什么公式？没关系

利用正规方程可以很简单地通过矩阵运算解决上述回归问题，因此我们找到normalEqn.m文件进行完善

theta = pinv(X'*X)*X'*y;

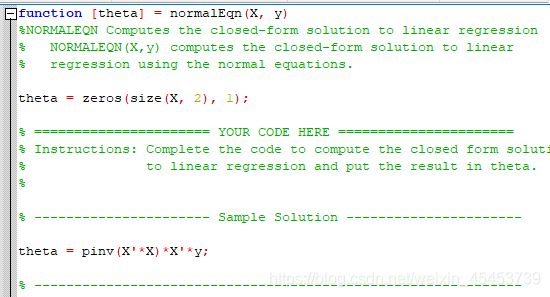
同样的，我们这时候就可以运行一下ex1_multi.m文件查看结果，同样得到了相关的参数值

但是你发现这为什么与上述的梯度下降求出来的参数不一样呢？正常现象，因为该处是利用原始数据进行计算，因此在求预测值时候我们只需要用原始值即可

price = [1,1650,3] * theta;

下面来看看利用正规方程所求得的房价的预测结果

至此，你也应该掌握了利用正规方程求线性回归参数的方法了，但，这预测值怎么好像跟梯度下降的有点偏差？可不可以避免呢？是谁的问题呢？

3.3 迭代次数与学习率

在梯度下降算法中，我们需要选定迭代次数与学习率，以控制梯度下降的整个过程，若迭代次数太少或学习率太小均可能造成拟合度不够，训练效果不够好的问题

因此，我们尝试修改梯度下降的迭代次数与学习率，看看是否能够得到正规方程中的值

• 迭代次数

在主程序文件ex1_multi.m中，保持学习率0.01不变，我们把迭代次数由400改为4000

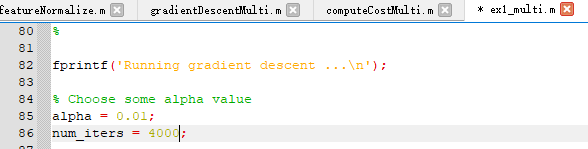
这时候可以看到在增加迭代次数后，该结果就非常接近正规方程得出的预测值

• 学习率

在主程序文件ex1_multi.m中，保持迭代次数400不变，我们把学习率由0.01改为0.1

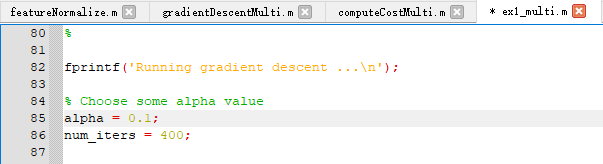
这时候可以看到在增加学习率后，该结果同样非常接近正规方程得出的预测值

结果表面，在梯度下降中选择合适的迭代次数与学习率才能得到较好的训练效果

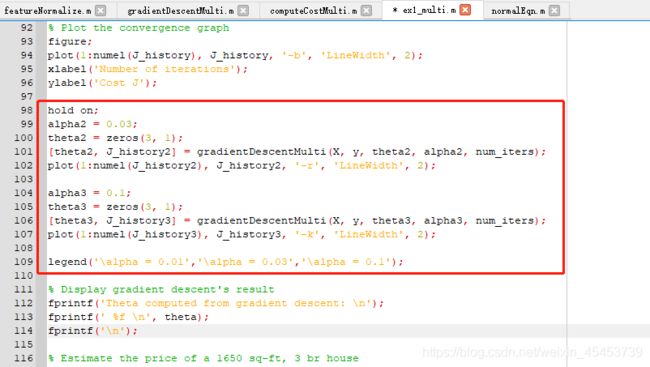
有兴趣的同学，也可以把不同学习率下，迭代次数对代价函数下降的影响图形绘出来，可以更直观感受，下面给出该绘图的示例代码（直接在ex1_multi.m中加入即可）

hold on;
alpha2 = 0.03;
theta2 = zeros(3, 1);
[theta2, J_history2] = gradientDescentMulti(X, y, theta2, alpha2, num_iters);
plot(1:numel(J_history2), J_history2, '-r', 'LineWidth', 2);

alpha3 = 0.1;
theta3 = zeros(3, 1);
[theta3, J_history3] = gradientDescentMulti(X, y, theta3, alpha3, num_iters);
plot(1:numel(J_history3), J_history3, '-k', 'LineWidth', 2);

legend('\alpha = 0.01','\alpha = 0.03','\alpha = 0.1');

下面看看运行的图像结果

至此，该课程练习的相关内容已经介绍完了，希望经过本文的练习讲解大家都对梯度下降、正规方程、线性回归等内容有较深入的理解