论文笔记：一种适用于NILM的暂态事件检测算法

目录

1. 前言

2. 双边CUSUM算法原理

3. 引入滑动窗

4. 算法参数

5. 算法流程

6. Next Action

---

1. 前言

        本文是对以下论文的阅读笔记，附有一定的解读和思考。

        牛卢璐，贾宏杰：一种适用于非侵入式负荷监测的暂态事件检测算法, 电力系统自动化2011

        负荷投切等过程中产生的暂态特征相比用电设备的稳态特征，能为负荷辨识提供更多的有用信息，因此利用负荷暂态特征来辨识负荷及其运行状态是ＮＩＬＭ 发展的一个主流方向. 基于暂态特征进行负荷辨识，准确掌握电气设备的投切时刻是其关键，为此，该论文提出了一种有效的暂态事件检测算法———基于滑动窗的双边累积和（ｃｕｍｕｌａｔｉｖｅ　ｓｕｍ，ＣＵＳＵＭ）暂态事件自动检测算法，它能根据相关信号（如电压、电流、有功、无功等）准确检测到电气设备投切等引起的系统暂态过程，具有算法简单、抗干扰能力强的特点。

2. 双边CUSUM算法原理

        考察随机时间序列：

        其中，Ak和Bk为数学期望为0的随机变量。D为变点（发生变化的时刻）前后的均值变化量。 为发生变化的时刻， 表示指示函数(Indicator function)。

        该论文考虑基于非参数化的双边ＣＵＳＵＭ 变点检测算法确定负荷的投切时刻。其算法原理如下。

        定义：

 

        假设稳态时的采样序列均值为μ０，本算法的要点如下：

        １）当序列处于稳态时，ＣＵＳＵＭ 统计量和是一个在０附近随机波动的变量，即以０为均值的随机变量（注意，疑原文此处有误。由以上递推关系式可知，和不会小于0）。

        ２）若序列发生突变，出现正向偏移，偏移后的序列均值上升为μ１＞μ０＋β，那么，这个向上的、正的偏移就会不断累积到统计量中，不断增大；反之，如果序列发生负向偏移，偏移后的序列均值下降为μ１＜μ０－β，那么向下的、负的偏移就会不断累积到统计量中，不断增大。

         ３）当 ＞０，但尚未达到阈值ｈ时，令检测延迟时间 ＝ ＋１，否则令 ＝０。当 ＞ｈ 时，一个均值增加的暂态事件被检测出来，采样序列突变的发生时刻τ可以倒推估计为。类似地，当 ＞０，但尚未达到阈值ｈ 时，令检测延迟时间，否则令。当 ＞ｈ 时，一个均值减少的暂态事件被检测出来，采样序列突变的发生时刻τ可以倒推估计为。

3. 引入滑动窗

        上述双边ＣＵＳＵＭ 算法的优点是算法简单、易于实现，但该算法的应用前提是已知采样序列均值。对于负荷不断变化的实际电力系统，均值也是不断变化的，为此论文通过引入滑动窗口来对ＣＵＳＵＭ 算法进行改进。基本思想：

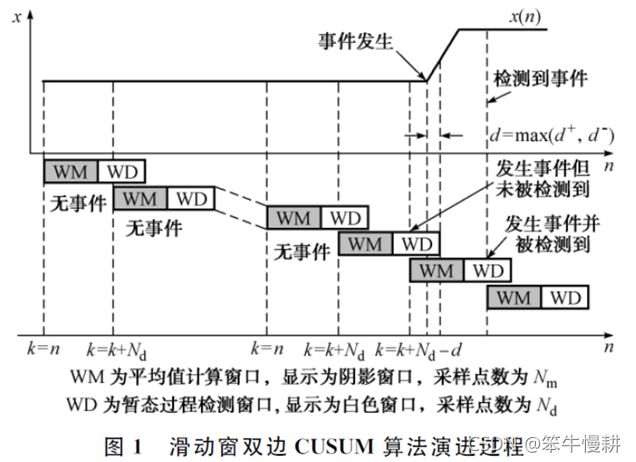
1. 每次针对一个时间窗口内的时间序列进行变点检测，该时间窗口又分为前后两个子窗口：WM(window for mean)用于评估均值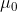，WD(window for detection)用于检测变化。
2. 检测完一个窗口后，移动到下一个窗口进行相同的检测。前后两个窗口有一定的overlap。这里分两种情况：
   1. 如果前一个窗口没有检测到变化事件，则后一个窗口的起始点位置按如下所述方式计算
   2. 如果前一个窗口检测到变化事件，则后一个窗口从检测到的事件时刻开始

         为了防止检测过程中某些暂态事件被漏检，当前ＷＭ 窗口的末端与“上一ＷＤ窗口减去检测延迟ｄ后”对齐（注意，原文的示意图[如下]并没有正确地表现出这种情况）。这是因为，当暂态事件发生在ＷＤ检测窗口的尾部时，   和可能没有足够的时间上升到阈值ｈ，此时平均值窗口ＷＭ 的末端被特意调整放置在暂态事件可能的发生时刻之前，这样可以在新的窗口进一步验证是否真正有暂态事件发生，从而降低了漏检的可能性。

        注意，上图的横轴上的关于k的变化与对应的WM和WD的文字说明似乎并不相符。 

4. 算法参数

        以上算法中有两个参数：h和。这两个参数的实际的物理含义是什么呢？

        h是判决门限，当变化累计量g+或g-超过该门限时即判定为检测到事件发生。与测量噪声的方差有关，即期望模型所能检测到的（当前值相对于均值的）最小变化量。只有大于的变化才会导致g+或g-增长，小于\beta的变化会导致g+或g-变小（此处有疑问，感觉是不是可以改进?）。

         考虑一个阶跃性跳变，并考虑期望模型能够检测出的最小阶跃性跳变为，以及最大允许检测延迟(采样点数)。参考下图的阴影区域，当信号量阶跃性跳变到时，每个时刻被计入累计量的有效变化为，要在个样点内满足判决条件的话，就要求h和必须满足以下条件：

 

        以上考虑的是阶跃性跳变的理想情况，但是实际电力系统中，负荷功率消耗的有功功率一般是缓慢上升而不是阶跃变化的。上述阴影部分并不是一个矩形，此外噪声水平等因素也比较难确定，特引入系数和来修正阴影部分面积，式（４）可以进一步改写为：

5. 算法流程

        基于以上讨论，可以得到算法流程如下图所示：

 

         根据对Δｍｉｎ和Nｍａｘ以及抗干扰能力的要求，可以对ｈ等参数进行初始化，然后根据不断读入的数据块来判断系统是否发生了扰动。其中，数据块的采样点数为Ｎ，ＷＭ 和ＷＤ窗口中采样点数分别为Ｎｍ和Ｎｄ，算法检测到暂态事件的时刻为ｋｅｖｅｎｔ，暂态事件发生的起始时刻的估计值为ｋｓｔａｒｔ。Ｎｍ的大小表示平均值计算窗口样本个数的多少，它的取值要能尽量代表正常状态下的特征。Ｎｄ表示检测窗口样本个数的多少，Ｎｄ值不能太大，否则会由于检测窗口过长而引入较长的检测延迟。

 

6. Next Action

        如上所述，论文中的描述、配图和算法流程图都存在一些疑点，需要进一步确认。

        当“爬坡”事件较长时，以上算法似乎（需要实际仿真验证）会导致多次重复触发检测到事件的响应，如何正确识别出它们实际上是属于同一个事件呢？

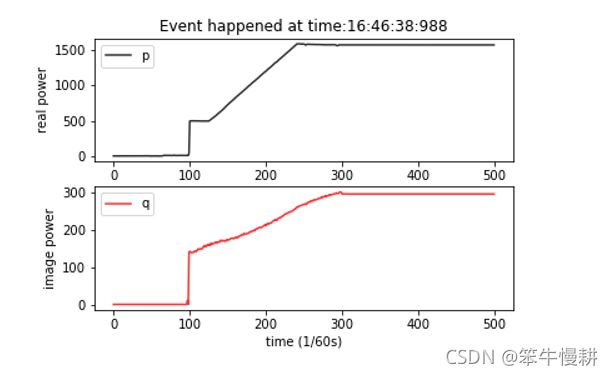
        进一步，“爬坡”的起点和终点其实都应该被正确地识别为变化事件。但是对于某些实际应用来说，可能需要把整个“爬坡”过程当作一个完整的事件来看待（如下图所示），换句话说，如何识别出一个变化事件的起点和终点呢？